Условие задания. На рис.1 изображена расчетная схема балки, расположенной в горизонтальной плоскости OYZ.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
Кафедра механики
Задание для самостоятельной работы «Определение реакций опор твердого тела (Плоская произвольная система сил)»
Вариант: 4
Выполнил студент группы: Сиб15Д1
Братишко Виктор Александрович 09.02.16
Проверил преподаватель:
Лукин Александр Михайлович _______________
Омск СибАДИ 2016
Условие задания. На рис.1 изображена расчетная схема балки, расположенной в горизонтальной плоскости OYZ.
Рисунок
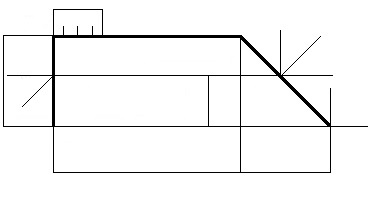 Рис. 1
Рис. 1
Балка загружена активными нагрузками P 1, P 2, M, q, где P 1 и P 2 – сосредоточенные силы; М – алгебраический момент пары сил; q – интенсивность распределенной нагрузки.
Дано: модуль Р1 активной силы Р2 равен 10 кН; Р2 = 10 кН; М = 6 кН∙м; q = 2 кН/м. Определить реакции внешних связей в точке B,реакцию опоры в точке A.
Задание. Используя основную форму уравнений равновесия для плоской произвольной системы сил, определить реакции внешних связей, наложенных на балку. Применяя другую форму уравнений равновесия, проверить правильность расчётов.
Решение.
Определение реакций внешних связей для рассматриваемой балки проводится согласно следующему алгоритму.
1. Выбирается система отсчета. По условию задания система отсчета OYZ показана на рис. 1.
2. Выделяется тело, равновесие которого рассматривается. В нашем случае таким телом является балка, изображенная на рис. 1.
3. К балке прикладываются активные нагрузки. По условию задачи активные нагрузки известны. Так как задана распределенная нагрузка с интенсивностью q, то ее приводят к сосредоточенной силе Q, модуль которой определяют по формуле Q = q∙L, где L – размер, на котором приложена распределенная нагрузка. В нашем случае L = 2 м. Исходя из этого, имеем
Q = q∙L = 2∙2 = 4 кН.
Сосредоточенную силу Q прикладывают к телу и показывают размер, на котором она приложена. Таким образом, на балку действуют следующие активные нагрузки: P 1, P 2, Q – активные силы; активная пара сил с алгебраическим моментом М.
Рисунок
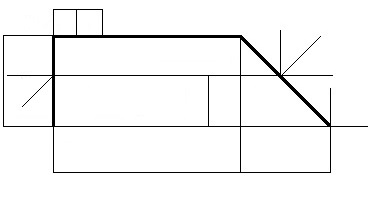 Рис. 2
Рис. 2
4. Согласно аксиоме связей внешние связи, наложенные на механическую систему в точке А, отбрасывают и показывают реакции внешних связей XA и YA, а также пару сил с алгебраическим моментом MA. Таким образом, на балку действуют внешние нагрузки, состоящие из активных нагрузок: P, Q, М и реакции внешних связей: XA, YA, М A.
5. Так как система внешних сил, действующих на тело, является плоской и произвольной, то записывают три уравнения равновесия:
| ƩFiEOY + ƩRiEOY = 0 = -P1∙cos(30°) + P2∙cos(45°) + YB = 0; | (1) |
| ƩFiEOZ + ƩRiEOZ = 0 = P1∙sin(30°) + RA – Q + P2∙sin(45°) + ZB = 0; | (2) |
| ƩMA(FiE) + ƩMA(RiE) = 0 = P1∙cos(30°)∙1-Q∙1-M + P1∙sin(45°) ∙5-P2∙cos(45°) ∙1+ZB *6 = 0, | (3) |
где ƩFiEOY, ƩFiEOZ – суммы проекций активных сил FiE на координатные оси OY, OZ системы отсчета OYZ; ƩRiEOY, ƩRiEOZ – суммы проекций реакции RiE внешних связей на координатные оси OY, OZ системы отсчета OYZ; YA, ZA – модули реакций YA, ZA жесткой заделки в точке А на координатные оси OX, OY системы отсчета OYZ; ƩMA(FiE) – сумма моментов активных сил FiE относительно точки А; ƩMA(RiE) – сумма моментов реакций RiE внешних связей относительно точки А.
При составлении выражений (1), (2), (3) использована первая форма уравнений равновесия. Эти уравнения решают в наиболее удобной последовательности и находят проекции неизвестных реакций на координатные оси системы отсчета OYZ или модули этих реакций.
Из уравнения (1) YB = P1∙cos(30°) -P2∙cos(45°) = 10∙0,15 –
- 10∙0,52 = -3,700 кН.
Из уравнения (3) ZB=(-P1∙cos(30°)∙1+Q∙1+M-P1∙sin(45°) ∙5+P2∙cos(45°) ∙1)/6 = -10∙0,15∙1+4∙1+6-10∙0,85∙5+10∙0,52∙1=-4,800кН.
Из уравнения (2) RA =-P1∙sin(30°)+ Q - P2∙sin(45°) + ZB =-10∙(-0,98)+4-10∙0,85+(-4,8)=0,5кН.
Согласно условию задания необходимо произвести проверку правильности проведенных расчетов. С целью такой проверки изобразим рассматриваемую балку в упрощенном варианте (рис. 3).
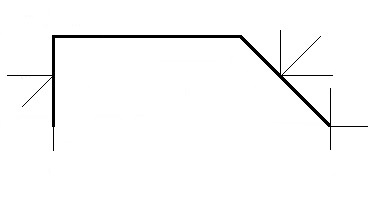 Рис. 3
Рис. 3
рисунок
Силы P 1 и P 2 разложены на составляющие силы P 1 OY и P 1 OZ, P 2 OY и P 2 OZ по координатным осям. Это упрощает проецирование сил P 1 и P 2 на координатные оси системы отсчета OYZ. Используя третью форму уравнений равновесия для плоской произвольной системы сил, запишем уравнение для рассматриваемой балки:
| ƩMB(FiE) + ƩMB(RiE) = 0 = -Q∙1-Р2∙sin(45°)∙5 + ZB + YB – M =0. | (4) |
где ƩMC(FiE) – сумма моментов активных сил FiE относительно точки C; ƩMC(RiE) – сумма моментов реакций RiE внешних связей относительно точки C.
Подставляя найденные значения реакций YA, ZA и МА в выражение (4) и вычислив, получим:
ƩMC(FiE) + ƩMC(RiE) = 0 = -4 – 8,5∙5 + 4,8∙6 -3,7 -6 = 6-6=0.
Проведенная проверка подтвердила правильность результатов расчетов. Результаты вычислений помещают в таблицу.
| Реакции и их размерность | YB, кН | ZB, кН | RA, кН∙м |
| Численные значения реакций | -3,700кН | -4,800кН | 500кН |








