Аналитический способ задания сил на плоскости

Дата: 2025-05-25; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Силу F на плоскости Оxy можно задать через ее проекции Fх и Fу на оси прямоугольной системы координат по правилу сложения векторов, определив точку А (xA, yA) приложения силы: F = Fх X i + Fу Y j, где i, j - единичные векторы. Модуль силы F и углы, которые она образует с координатными осями вычисляются по формулам: F = [Fх2+ Fу2 + Fz2]^1/2;

cos (F, i) = F х /F, cos (F, j) = Fy/F.

Аналитический способ сложения сил: Воспользуемся теоремой: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Спроецируем равенство R = SFk на оси прямоугольной системы координат Оху, получим R х = SFkx , Ry = SFky , ( k = 1, 2, .., n )

где Fkx, Fky - проекции k-ой силы Fk на оси Ох и Оу соответственно. Тогда на плоскости Оху вектор R равные геометрической сумме слагаемых сил F1, F2, ..., Fn определяется по формулам: R = RхЧi + RуЧj;

R = [R х 2+ R у 2]1/2;

cos (R, i) = R х /R, cos (R, j) = R у /R.

5) Система сходящийся сил и их равнодействующая

Система сходящихся сил. Приведение к равнодействующей. Вычисление равнодействующей.

Пусть, к абсолютно твердому телу приложена система N сил (F1, F2, ... FN), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной равнодействующей силе R.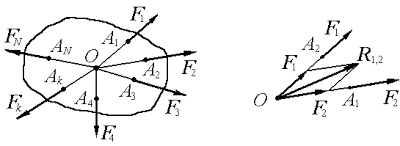

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами. Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника или R.

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.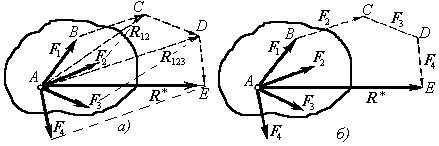

6) Геометрическое условие равновесия системы и сходящихся сил

Геометрическое условие равновесия. Так как равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т. е. когда много­угольник замкнется.

Смотри 3 вопрос

7) Аналитическое условие равновесия систем сходящихся сил

Смотри 4 вопрос R_х = SF_kх = 0, R_у = SF_ky = 0.

8) Момент силы относительно центра

Момент силы относительно центра О называется векторная величина м0= векторному произведению вектора R на вектор F.

m0=F x R

характеризует вращательный эффект F относительно центра О.

момент относительно центра не измениться при переносе силы вдоль линии ее действия

если линия действия F пересекает центр О то момент = 0

9) Алгебраический момент силы относительно точки плоскости

= произведению F на плечо L взятое с определенным знаком

m=+-F x L

10) Теорема о парралельном переносе сил

Силу можно перенести параллельно линии ее действия, при этом нужно добавить пару сил с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.

11) Теорема Пуансо

Любая система сил действующая на абсолютно твердое тело при ее приведении к произвольному центру заменяется на одну R (главный вектор системы сил) и пару сил с моментом М (главный момент системы относительно центра О)

{F1,F2,F3}={R,M}

R=F1+F2+F3 M=∑m(F0)

12) Теорема Вариньона

Если система сил, приложенных к абсолютно твердому телу, имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси). m ( R )=∑ m ( F ) { R }={ F 1…. Fn }

13) Условия равновесия твердого тела под действием произвольной системы сил

Для равновесия произвольной системы сил, необходимо, чтобы суммы проекций всех сил на оси декартовой системы координат равнялись нулю и суммы моментов всех сил относительно этих осей также равнялись нулю.

14) Момент силы относительно оси

Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью. Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

15) Аналитические выражения моментов силы относительно декартовых осей

Момент сил относительно декартовых осей координат (проекции момента силы на эти оси).

| i j k |

M0(F) = r * F = | x y z | = (y*Fz - z*Fy)*i + (z*Fx - x*Fz)*j + (x*Fy - y*Fx)*k = Mox(F)*i + Moy(F)*j + Moz(F)*k

| Fx Fy Fz |

Mox(F)=y*Fz - z*Fy

Moy(F)=z*Fx - x*Fz

Moz(F)=x*Fy - y*Fx

16) Правило вычисления момента силы относительно оси

Следует спроецировать силу на плоскость перпенд-ую данной оси, а за тем определить алгебраический момент силы (полученной проекции) относительно точки пересечения данной оси с этой плоскостью.

17) Вычисление главного вектора и момента системы сил

Главный вектор пространственной системы сил определяется так же, как в плоской статике: это вектор , равный векторной сумме всех сил системы: R= F1+F2F+F3=∑( F )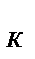

Главный момент системы сил называется вектор 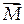₀, равный сумме векторных моментов всех сил относительно некого центра 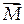=M 0( F )+ M 0( F 2)=∑ M 0( F )

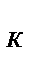18) Аналитические условия равновесия для плоских и пространственных систем сил

Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то равнодействующая этой системы равна нулю, следовательно проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил: ΣX = 0; ΣY = 0; ΣZ = 0.

Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю. ΣX = 0; ΣY = 0.

Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.

19)Частные случаи привидение пространственной системы сил к центру

Любая система сил, действующих на абсолютно твердое тело, может быть заменена одной силой R, равной главному вектору этой системы сил и приложенной к произвольно выбранному центру О, и одной парой сил с векторным моментом L_O, равным главному моменту системы сил относительно центра О.

Такая эквивалентная замена данной системы сил силой R и парой сил с моментом L_O называют приведением системы сил к центу О.

В результате приведения пространственной системы сил к произвольному центру О возможны следующие случаи, зависящие от векторов R и L_O:

1. если R = 0, L_O = 0, то заданная система является равновесной;

2. если хотя бы одна из величин R или L_O не равна нулю, то система сил не находится в равновесии.
При этом:

o Eсли R = 0 и L_O 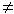0, то система сил приводится к одной паре сил с моментом L_O. В этом случае величина момента L_O не зависит от выбора центра О.

o Eсли R 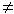0, L_O = 0, то система сил приводится к равнодействующей силе R^* = R, линия действия которой проходит через центр О.

o Eсли R 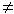0, L_O 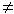0 и эти векторы взаимно перпендикулярны, то система сил также приводится к равнодействующей силе R^* = R, но линия ее действия не проходит через центр О.

20)Центр тяжести твердого тела

Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела.

Кинематика

1) Способы задания движения точки и уравнения движения

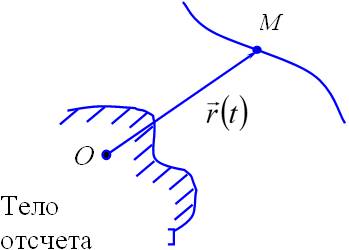
Векторный

Положение точки определяется радиус-вектором, проведенным из неподвижной точки, связанной с телом отсчета: 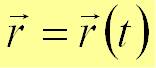− векторное уравнение движения точки.

Координатный

В этом случае задаются координаты точки как функции времени:

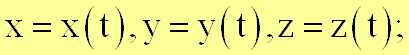
Естественный для задания движения надо знать

Траекторию движения

Выбрать начало отсчета

Задать полож направление движения

Знать f изменения криволинейной координаты

S=S(t)

2) Скорость и ускорение точки при векторном способе задания движения

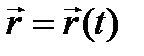
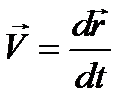
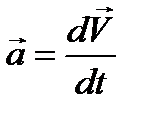Так же в зависимости от угла (а) зависит характер движения

а<90 ускорение, а>90 замедление, а=90 равномерное

3)Скорость и ускорение точки при координатном способе задания движения

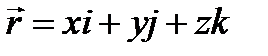
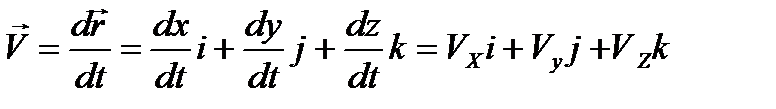
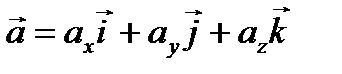
4)Скорость и ускорение точки при естественном способе задания движения

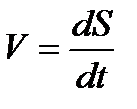
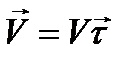
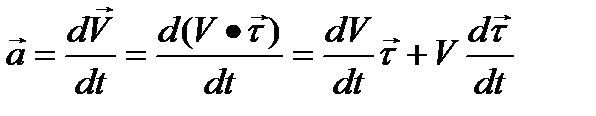
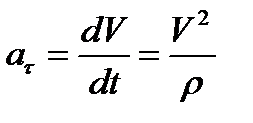
aτ=τ ⋅ dV/dt=τ ⋅ d2S/dt2, aτ=dV/dt=τ ⋅ d2S/dt2- касательное ускорение; оно характеризует быстроту изменения величины скорости точки;

an=n ⋅ V2/ρ, an=V2/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости;

ρ - радиус кривизны траектории в данной точке (для окружности:ρ=R , для прямой линии ρ=∞ ).

5)Поступательное движение твердого тела

Это движение, при котором любая прямая проведенная в теле, при его движении остается парралельным своему первоначальному положению.

При этом движении все его точки описывают одинаковые траектории и в каждый момент времени имеют равную скорость и ускорение.

6) Вращательное движение тела вокруг не подвижной оси уравнение вращательного движения

Это такое движение при котором 2-е точки данного тела неподвижны Уравнение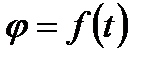

7) Угловая скорость и ускорение вращательного тела

Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.

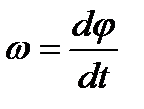
Угловым ускорением называют степень изменения угловой скорости.

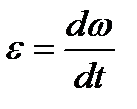
8) Скорость и ускорение точки тела при вращательном движении вокруг не подвижной оси

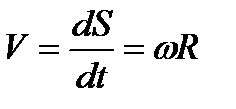
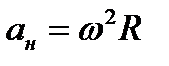
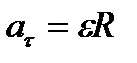
9) Выражение скорости и ускорения точки вращающегося тела в виде векторного произведения

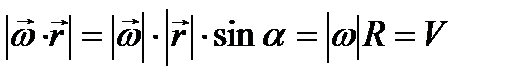
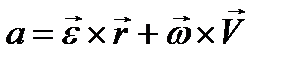
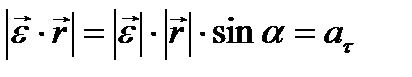
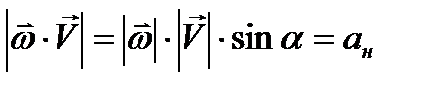
10) Плоскопараллельное движение. Уравнение движения плоской фигуры

Это такое движение, при котором все точки тела движутся в плоскостях параллельно неподвижной плоскость

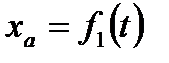
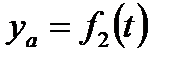
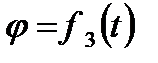
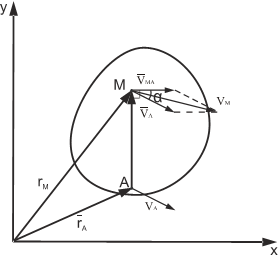
11) Теорема о скоростях точек плоской фигуры.

V любой точки плоской фигуры = геометр. сумме скорости полюса и скорости точки во вращении вокруг данного полюса

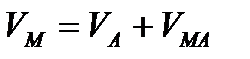
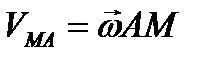
12) Теорема о проекциях скоростей двух точек плоской фигуры

Проекции скоростей 2-х точек плоской фигуры на ось проходящую через эти 2-е точки равны.

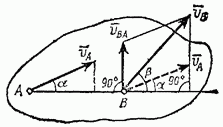
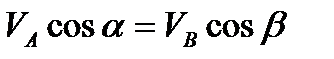
13) Мгновенный центр скоростей.

Это точка р плоской фигуры , V которой =0 в данный момент времени

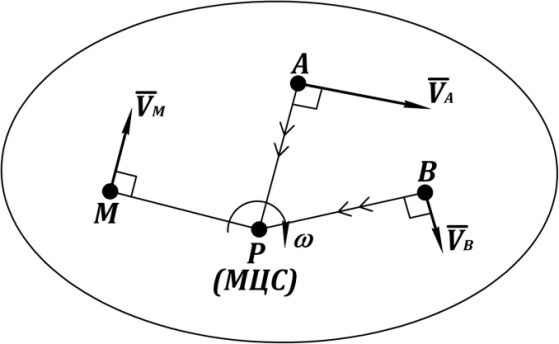
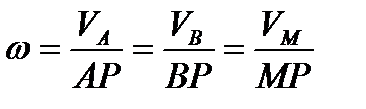
14) Определение скоростей точек и угловой скорости плоской фигуры с помощью мгновенного центра скоростей И 15) Способы определения положения мгновенного центра скоростей.

Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

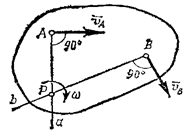
Легко убедиться, что если фигура движется не поступательно, то такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоской фигуры имеют скорост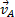и и 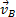, не параллельные друг другу (рис.33). Тогда точка Р, лежащая на пересечении перпендикуляров Аа к вектору 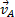и Вb к вектору 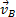, и будет мгновенным центром скоростей так как 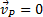. В самом деле, если допустить, что 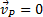, то по теореме о проекциях скоростей вектор 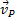должен быть одновременно перпендикулярен и АР (так как 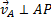) и ВР (так как 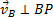), что невозможно. Из той же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю.

Если теперь в момент времени 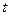взять точку Р за полюс, то скорость точки А будет 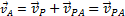так как 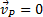. Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом

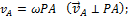
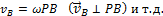
Из равенств, следует еще, что 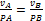точек плоской фигуры пропорциональны их расстояниям от МЦС.

Полученные результаты приводят к следующим выводам.

1. Для определения мгновенного центра скоростей надо знать только направления скоросте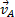й и 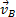каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).

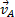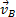2. Для определения скорости любой точки плоской фигуры, надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, восставив из точек А и В перпендикуляры к и , построим мгновенный центр скоростей Р и по направлению 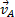определим направление поворота фигуры. После этого, зная 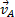, найдем скорость 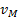любой точки М плоской фигуры. Направлен вектор 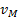перпендикулярно РМ в сторону поворота фигуры.

3. Угловая скорость 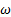плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р: .

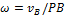Рассмотрим некоторые частные случаи определения мгновенного центра скоростей.

а) Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого неподвижного, то точка Р катящегося тела, касающаяся неподвижной поверхности (рис.34), имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю ( 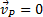), и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.

б) Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна 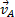(рис.35,а), то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны 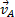. При этом из теоремы о проекциях скоростей следует, что 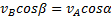т. е. 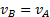; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость 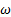тела в этот момент времени, как видно равна нулю.

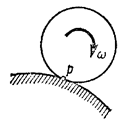рис 34 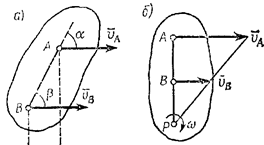рис 35

в) Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна 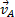, то мгновенный центр скоростей Р определяется построением, показанным на рис. 35,б. Справедливость построений следует из пропорции. В этом случае, в отличие от предыдущих, для нахождения центра Р надо кроме направлений знать еще и модули скоростей .

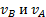г) Если известны вектор скорости 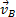какой-нибудь точки В фигуры и ее угловая скорость 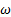, то положение мгновенного центра скоростей Р, лежащего на перпендикулярно к 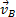(рис.35,б), можно найти как .

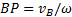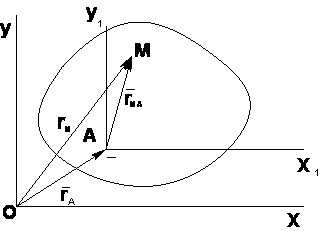
16) Теорема об ускорениях точек плоской фигуры.

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.

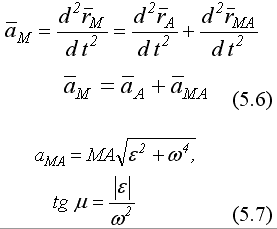
17) Абсолютное, относительное и переносное движение точки.

Движение точки по отношению к подвижной системы координат называется относительным.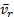

Движение тела вместе с точкой М по отношению к неподвижной системе называется переносным (Vе)

Движение точки М по отношению к неподвижной системе называется абсолютным движением (Va)

18) Теорема о сложении скоростей точки при ее составном движении.

Утверждает, что при сложном движении материальной точки её абсолютная скорость равна сумме относительной и переносной скоростей.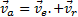

19)Теорема Кориолиса о сложении ускорений точек

Абсолютное ускорение в сложном движении = геометрической сумме переносного, относительного движения и ускорения Кориолиса.

20) Модуль и направление ускорения Кориолиса. Случаи отсутствия ускорения Кориолиса при сложном движении.

Сначала определяем направление относительной скорости затем строим угловую скорость.

Вектор относительной скорости спроецируем на плоскость перпендикулярную угловой скорости и поворачиваем на 90 градусов проекцию в сторону поворота угловой скорости -это и будет ускорение Кориолиса

Когда ускорение Кориолиса =0

1) угловая скорость =0 в случае когда переностное движение является поступательным

2)относительная скорость =0 в точках остановки относительного движения

3) sinα = 0 когда векторы колиниарны ( отн и перен скоростей)

Динамика

1) Дифференциальные уравнения движения материальной точки в векторной форме.

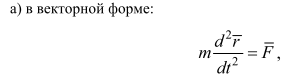
2) Дифференциальные уравнения движения материальной точки в декартовых координатах.

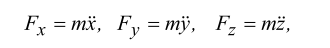
3) Естественные уравнения движения материальной точки.

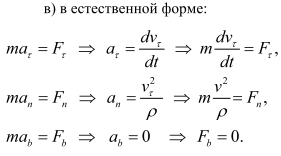
4) Две задачи динамики материальной точки.

5) Решение второй задачи динамики точки. Определение постоянных интегрирования.

Второй или обратной называется задача, в которой по заданным силам и массе материальной точки определяется ее движение. Для решения задачи надо выполнить следующие операции.

● Построить расчетную схему. Для этого прежде всего надо выбрать систему координат. В случае произвольного движения точки в пространстве следует выбрать систему координат 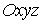. Положение начала координат 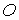указывается в условии задачи или выбирается в начальном положении движущейся материальной точки.

● Затем в принятой системе координат надо изобразить предполагаемую траекторию точки и отметить на ней начальное положение точки 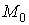, изобразить начальную скорость 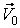. Следует отметить также произвольное положение точки 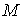, обозначить ее координаты 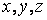; изобразить все силы, действующие на материальную точку в этом произвольном положении. Если точка движется по плоскости, то следует выбирать систему координат . Для прямолинейного движения материальной точки достаточно выбрать одну координатную ось, которая совмещается с траекторией точки; при этом за положительное направление оси следует принять направление начальной скорости .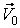

Уточнить начальные условия движения точки, т. е. из условия задчи при 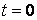определить 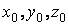– координаты точки в начале движения; 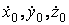– проекции начальной скорости на оси координат.

Составить дифференциальные уравнения движения точки в форме (1.2):

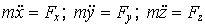
– это дифференциальные уравнения второго порядка.

Определить законы движения вдоль координатных осей; т. е. найти вторые интегралы уравнений (1.2):

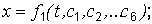
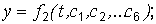
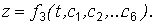
Постоянные интегрирования 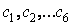находятся с использованием начальных условий обычными для теории дифференциальных уравнений способами.

Основные виды дифференциальных уравнений и их интегрирование даны в приложении.

6) Дифференциальные урав-я относит-го движения матер-ой точки.

Составим основное уравнение динамики для точки 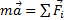, где абсолютное ускорение 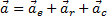. Поэтому уравнение будет таким .

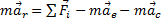Но 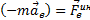- переносная сила инерции, 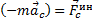- кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так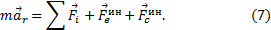

Спроектировав это векторное равенство на подвижные оси x1, y1, z1, имея в виду, что проекции вектора ускорения на оси – есть вторые производные от соответствующих координат по времени, получим дифференциальные уравнения относительного движения:

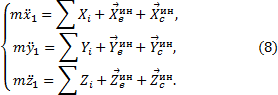
7. Принцип относительности классической механики.

8. Классификация сил мех системы. Свойство внутр сил

Силы, действующие на точки механической системы можно разделить на внешние и внутренние.

Внешними (F_i^E) называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.

Внутренними (F_i^I) называют силы, с которыми точки или тела одной системы действуют друг на друга.

Внутренние силы обладают следующими свойствами:

1.Геометрическая сумма всех внутренних сил системы равняется нулю. На основании третьего закона Ньютона силы взаимодействия между точками (телами) равны и противоположно направлены, следовательно, и сумма этих сил равна нулю (∑F_i^I=0).

2.Сумма моментов ( главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю.На основании теоремы Вариньона и главный момент внутренних сил относительно произвольного центра также равен нулю ( ∑M_i0F_i^I=0 ).

Из доказанных свойств не следует, однако, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызвать взаимные перемещения этих точек или тел. Уравновешенной вся совокупность внутренних сил будет у системы, представляющей собой абсолютно твердое тело.

9. Момент инерции тела относительно оси. Радиус инерции.

10. Теорема о моментах инерции тела относительно параллельных осей.

11. Моменты инерции однородного тонкого стержня, однородного тонкого кольца (тонскостенного полого цилиндра), сплошного кругового цилиндра (диска ).

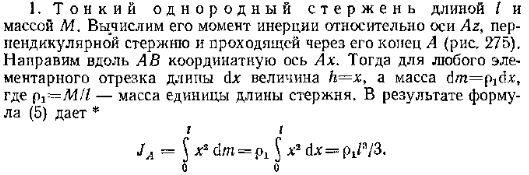
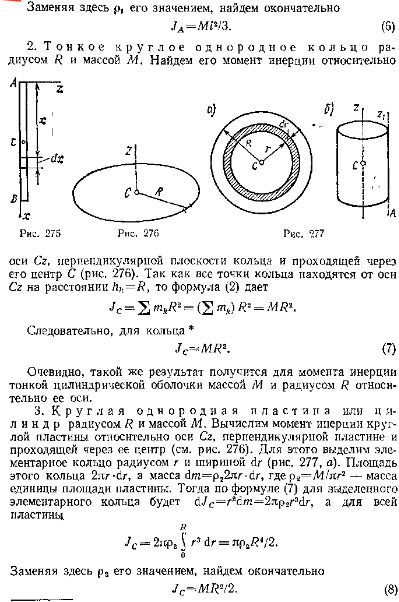
12) Диффер-ые урав-я движения механической системы в векторной форме и в проекциях на декартовые оси.

Рассмотрим систему, состоящую из n материальных точек. Выделим какую-нибудь точку системы с массой 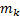. Обозначим равнодействующую всех приложенных к точке внешних сил (и активных и реак­ций связей) через 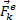, а равнодействующую всех внутренних сил – через 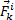. Если точка имеет при этом ускорение 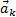, то по основному закону динамики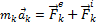

......

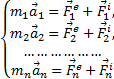
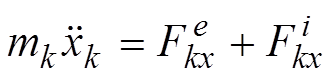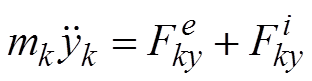
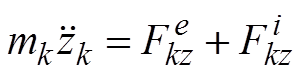
13) Теорема о движении центра масс механической системы.

Теорема о движении центра масс механической системы: центр масс механической системы движется как материальная точка с массой, равной массе системы, под действием главного вектора внешних сил, действующих на эту механическую систему.

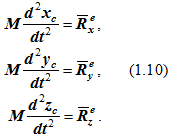
14) Количество движений материальной точки.

Количество движения мера механического движения, равная для материальной точки произведению её массы m на скорость v. mv — величина векторная, направленная так же, как скорость точки. Иногда К. д. называют ещё импульсом. При действии силы К. д. точки изменяется в общем случае и численно и по направлению; это изменение определяется вторым законом динамики. Q = mV – кол-во дв. мат. точки.

15) Элементарный импульс силы. Импульс силы за короткий промежуток времени.

Действие силы 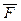на материальную точку в течении времени 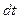можно охарактеризовать элементарным импульсом силы .

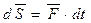За конечный промежуток времени эта величина равна определённому интегралу от элемен­тарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.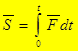

16. Теорема об изменении количества движения материальной точки в дифференциальной и конечной формах.

• В дифференциальной форме:

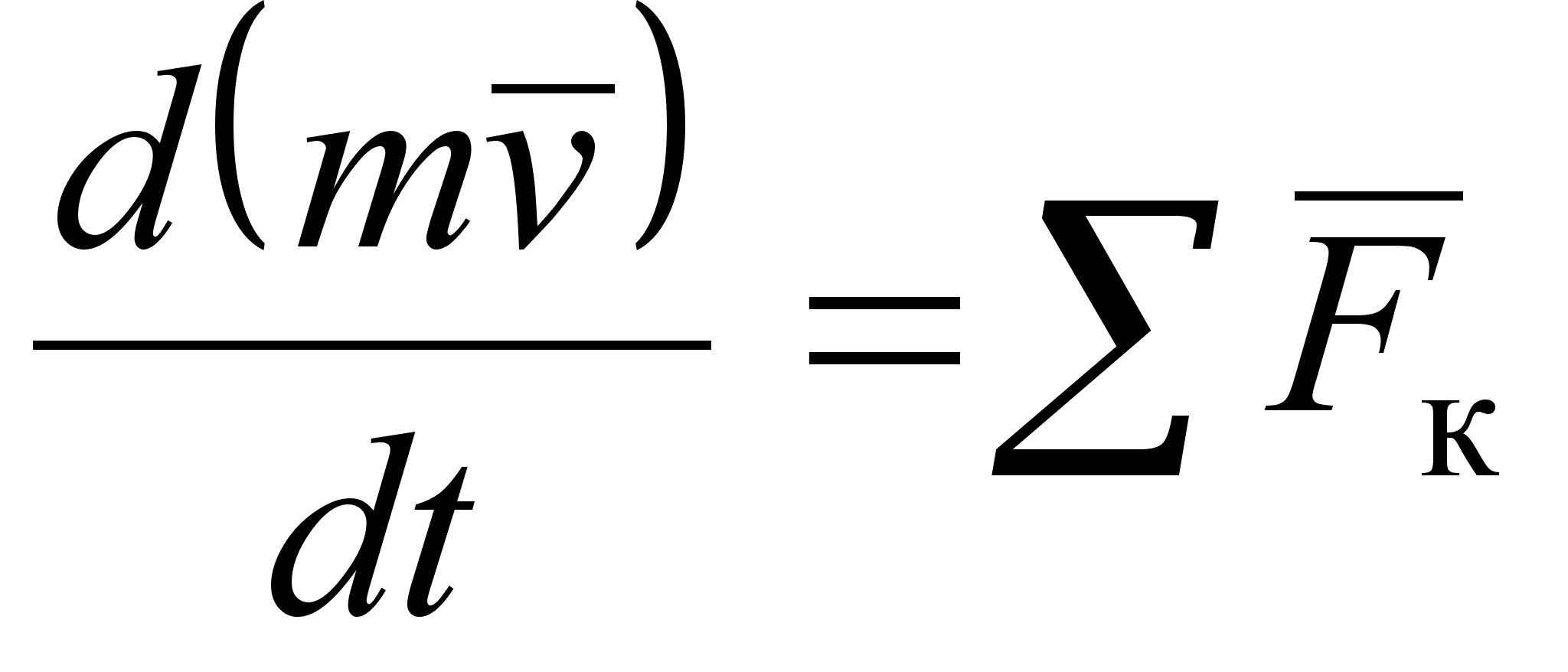
• В интегральной и конечной:

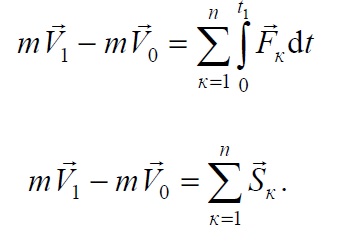
Где S_k – элементарный импульс силы

17. Главный вектор количества движения механической системы.

Количеством движения (главным вектором количества движения) механической системы называется вектор Q, равный геометрической сумме (главному вектору) количества движения точек системы:

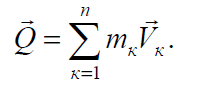
Или массе системы, умноженной на скорость ее центра масс

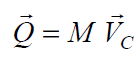
Следовательно, если центр масс остается неподвижным, то количество движения системы равно нулю, значит при вращении вокруг оси, проходящей через центр масс, количество движения будет равно нулю.

Называют главным вектором, а не равнодействующей, потому что векторы скоростей точек системы лежат не в сходящейся системе.

18. Теорема об изменении количества движения механической системы

«Изменение количества движения системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, действующих на систему за тот же промежуток времени».

В диф. форме: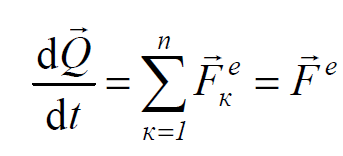

В конечной форме: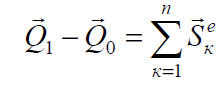

19. Закон сохранения количества движения системы

Это следствие из теоремы об изменении количества движения системы: «Если главный вектор внешних сил равен нулю, то количество движения механической системы будет постоянным»

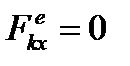
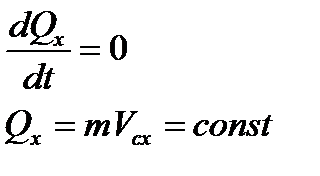
20. Момент количества движения материальной точки относительно центра и оси.

Моментом количества движения материальной точки относительно произвольного центра О называется вектор 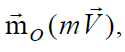определяемый равенством

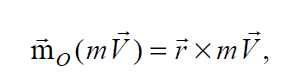
где r – радиус-вектор мат. точки, проведенный из центра О.

21. Кинетический момент механической системы относительно центра и оси.

Кинетический момент характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Главным вектором момента количества движения механической системы (кинематическим моментом) относительно произвольного центра О называется векторная величина 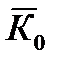равная сумме векторов моментов количеств движения всех точек системы

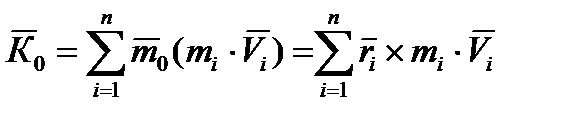
Спроецируем, данное векторное равенство на декартовы оси:

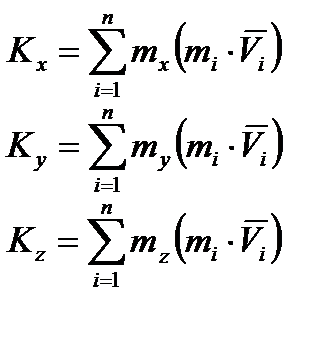
Покажем, что главный момент количества движения системы является характеристикой её вращательного движения:

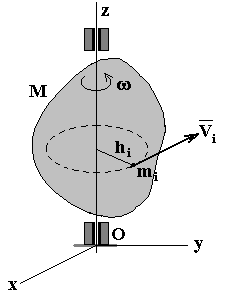
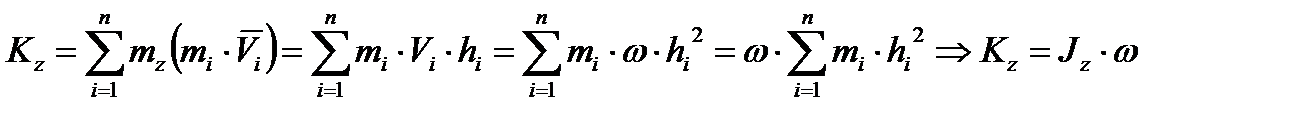
Следовательно, кинетический момент вращающегося тела относительно оси вращения равен произведению осевого момента на угловую скорость.

22. Кинетический момент вращающегося твердого тела относительно оси вращения.

Пусть твердое тело вращается вокруг неподвижной оси O_z с угловой скоростью 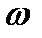. Выберем произвольную точку m_i в твердом теле и вычислим кинетический момент этого тела относительно оси вращения. По определению кинетического момента системы относительно оси имеем

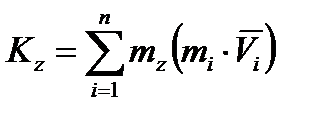
Но при вращении тела вокруг оси ,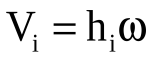

причём количество движения точки m_i ( m_iV_i ) ­ перпендикулярно отрезку h_i и находится в плоскости, перпендикулярной оси вращения O_z. Следовательно, момент количества движения относительно оси O_z для точки m_i: .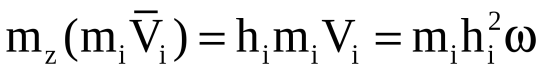

Для всего тела: ,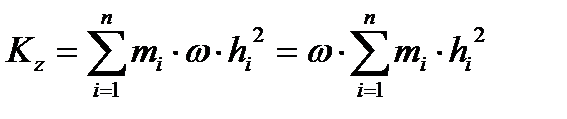

то есть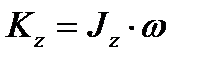

Кинетический момент вращающегося тела относительно оси вращения равен произведению угловой скорости тела на его момент инерции относительно оси вращения.

23. Теорема об изменении кинетического момента механической системы.

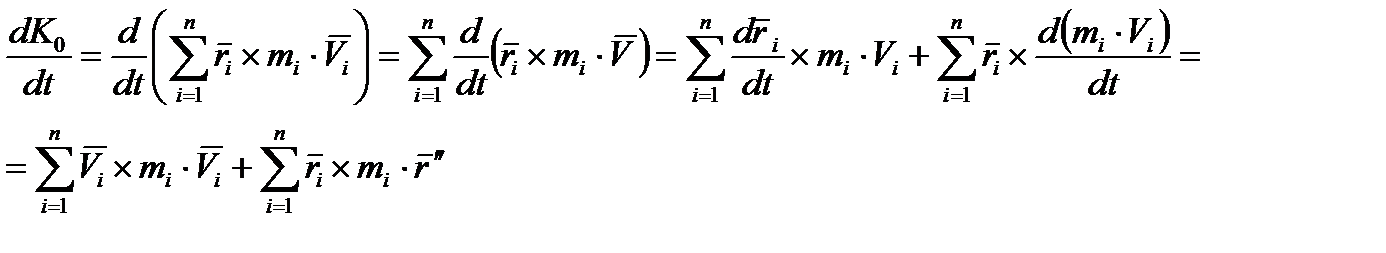
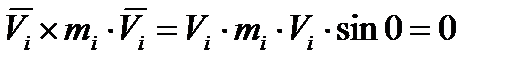
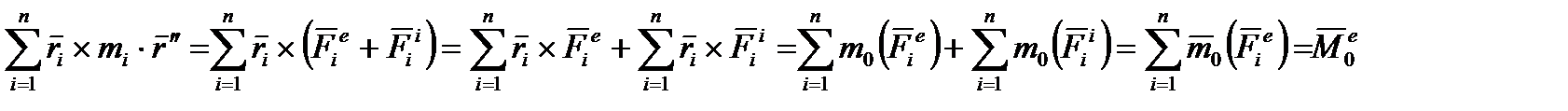
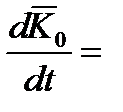
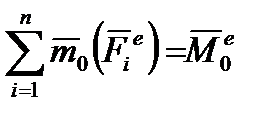
24. Законы сохранения кинетического момента системы.

Закон сохранения кинетического момента системы относительно неподвижной точки: если при движении системы сумма моментов внешних сил относительно неподвижной оси Z равна нулю, то кинетический момент системы относительно этой оси есть величина постоянная, т. е. если

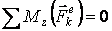, то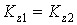

Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.

Поэтому 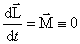, то есть

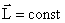или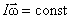

Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.

Законы сохранения момента количества движения.

1. Если линия действия равнодействующей приложенных к материальной точке сил все время проходит через некоторый неподвижный центр, то момент количества движения материальной точки остается постоянным.
2. Если момент равнодействующей приложенных к материальной точке сил относительно некоторой оси все время равняется нулю, то момент количества движения материальной точки относительно этой же оси остается постоянным.

25. Дифференциальные уравнения поступательного, вращательного и плоскопараллельного движения твёрдого тела. Дифференциальные уравнения поступательного движения твердого тела: 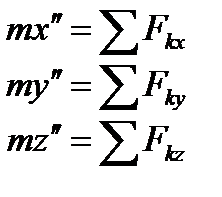– 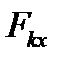и т.д. ­ проекции внешних сил.

Дифференциальные уравнения вращения твердого тела вокруг неподвижной оси:

поскольку 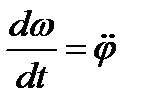, получаем .

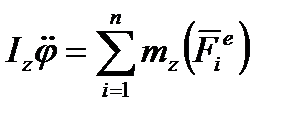Иногда вводиться обозначение 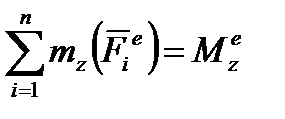, и величина 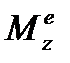вращающим моментом. Тогда как 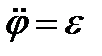угловое ускорение тела, то уравнение принимает вид

,

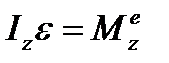то есть произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающему моменту.

Дифференциальные уравнения плоскопараллельного движения твёрдого тела:

Пусть твёрдое тело совершает плоское движение относительно неподвижной плоскости OXY под действием внешних сил и имеет угловое ускорение. Примем за полюс центр масс тела C. Есл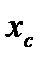и и ­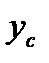 координаты центра масс в неподвижной системе отчёта OXY, то по теореме движения центра масс получим два дифференциальных уравнения, характеризующих поступательное движение тела вместе с центром масс C:

, .

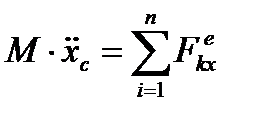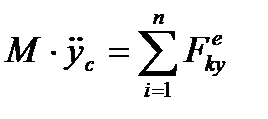Третье дифференциальное уравнение, определяющее вращательное движение вокруг оси 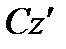получаем из .

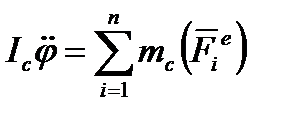Тогда окончательно находим дифференциальные уравнения плоскопараллельного движения твёрдого тела:

, , .

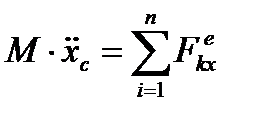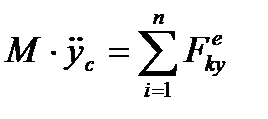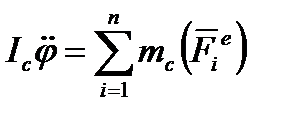26) Кинетическая энергия материальной точки и механической системы

Кинетической энергией системы называется скалярная величина, равная арифметиче­ской сумме кинетических энергий всех точек системы

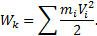
Для одной точки:

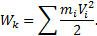
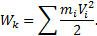
Если система состоит из нескольких тел, то ее кинетическая энергия равна сумме кинетических энергий этих тел:

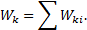
Кинетическая энергия – скалярная и всегда положительная величина.

27) Теорема Кёнига

При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела:

W_K∑=1/2 m V_c² +1/2 I_cω²

где m – масса всей системы, Ic − момент инерции тела относительно оси, проходящей через центр масс.

28) Кинетическая энергия твердого тела при поступательном, вращательном и плоскопараллельном движении

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости дви­жения центра масс. То есть, для любой точки V_i=V_C

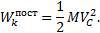
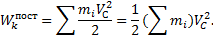
или

Таким образом, кинетическая энергия тела при поступатель­ном движении равна половине произведения массы тела на квад­рат скорости центра масс. От направления движения значение энергии не зависит.

2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (1 рисунок), то скорость любой его точки 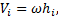где 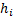– расстояние точки от оси вращения, а 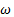– угло­вая скорость тела.

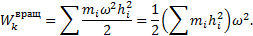
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Окончательно:

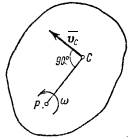
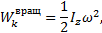
т.е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение энергия не зависит.

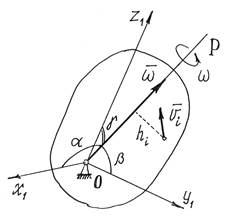При вращении тела вокруг неподвижной точки кинетическая энергия определяется как

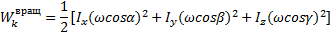
или

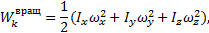
где 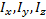– моменты инерции тела относительно главных осей инерции x₁, y₁, z₁ в неподвижной точке О; 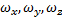– проекции вектора мгновенной угловой скорости 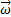на эти оси.

3. Плоскопараллельное движение. При этом движе­нии скорости всех точек тела в каждый момент времени распреде­лены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр ско­ростей Р (1 рисунок). Следовательно

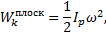
где 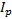- момент инерции тела относительно названной выше оси, 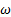- угловая скорость тела. Величина 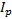в формуле будет перемен­ной, так как положение центра Р при движе­нии тела все время меняется. Введем вместо 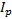постоянный момент инерции 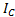, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса-Штейнера 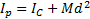, где d=PC. Подставим это выражение для 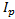. Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно, 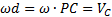, где 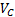- скорость центра масс С, окончательно найдем:

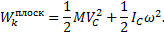
Следовательно, при плоскопараллельном движении кинетиче­ская энергия тела равна энергии поступательного движения со скоростью центра масс, сло­женной с кинетической энергией вращательного движения вокруг центра масс.

29) Элементарная работа силы. Работа силы на конечном перемещении точки её приложения. Мощность силы

Работа силы, мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения. Cила F численно и по направлению постоянна, а перемещение M₀M₁ прямолинейно/ A = F×s×cosa, где s = M₀M₁, α – угол между направлениями силы и перемещения. Единицы измерения A: джоуль kbи килограмм-сила на метр (1 кгс×м). В общем случае для вычисления работы силы силы вводится понятие элементарной работы dA = F×ds×cosa, где ds – элементарное перемещение, α – угол между направлениями силы и касательной к траектории точки её приложения, направленной в сторону перемещения. В декартовых координатах
dA = F_xdx + F_ydy + F_zdz,
где F_x, F_y, F_z – проекции силы на координатные оси, х, у, z – координаты точки её приложения.
Для сил, действующих на тело, имеющее неподвижную ось вращения, dA = M_zdj, где M_z – сумма моментов сил относительно оси вращения, j – угол поворота. Для сил давления dA = pdV, где р – давление, V – объём.
Работа силы на конечном перемещении определяется как интегральная сумма элементарных работ и при перемещении M₀M₁ выражается 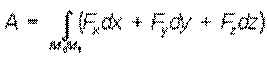криволинейным интегралом: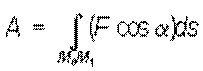

или

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность

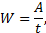
где t - время, в течение которого произведена работа A. В общем случае

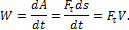
Следовательно, мощность равна произведению касательной состав­ляющей силы на скорость движения.

Единицей измерения мощности в системе СИ является ватт (1 вт=1 дж/сек).

30) Работа силы тяжести, силы упругости, силы приложенной к вращающемуся телу, силы трения скольжения. Работа постоянной силы на прямолинейном перемещении

1) Работа силы тяжести. Работа силы тяжести равна взятому со зна­ком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной. Работа силы тяжести не зависит от вида той траектории, по которой перемещается точка ее приложения.

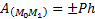
Силы, обла­дающие таким свойством, назы­ваются потенциальными.

2) Работа силы упругости. Работа силы упругости равна половине произведения коэффи­циента жесткости на разность квадратов начального и конеч­ного удлинений (или сжатий) пружины.

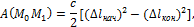
Работа будет положительной, когда 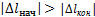, т. е. когда конец пружины перемещается к равновесному положению, и отрица­тельной, когда 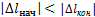, т.е. конец пружины удаляется от равновесия положения. Формула ос­тается справедливой и в случае, когда пе­ремещение точки М не является прямо­линейным.

Работа силы F зависит только от значе­ни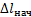й и 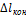и не зависит от вида траектории точки М. Сила упругости также является потенциальной.

3) Работа силы трения.

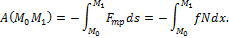
Если величина силы трения постоянна, то 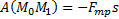, где s – длина дуги кривой М₀М₁ по которой перемещается точка.

Работа силы трения при скольжении всегда отрицательна. Величина этой работы зависит от длины дуги М₀М₁. Сила трения является силой непотенциальной.

4) Работа силы, приложенной к телу, вращающемуся вокруг неподвижной оси.

Если момент силы относительно оси 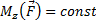, работа силы при повороте тела на угол 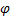равна

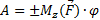
Знак работы определяется знаками момента силы и угла поворота. Если они одинаковы, работа положительная.

Из этой формулы следует и правило определения работы пары сил. Если пара с моментом m расположена в плоскости перпендикулярной оси вращения тела, то ее работа при повороте тела на угол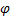

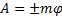
Если же пара сил действует в плоскости не перпендикулярной оси вращения, то ее надо заменить двумя парами. Одну расположить в плоскости перпендикулярной оси, другую – в плоскости параллельной оси. Моменты их определяются разложением вектора момента 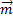по соответствующим направлениям: 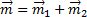. Конечно работу будет совершать только первая пара с моментом 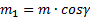, где 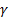– угол между вектором 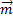и осью вращения z,

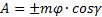
Работа постоянной силы на прямолинейном перемещении. Работа силы в общем случае численно равна произведению мо­дуля силы на длину пройденного им пути и на косинус угла между направлением силы и направлением перемещения

A = FScosα