1 ) Аксиомы статики. Задачи статики. Принцип освобождения от связей.
Статика
1 ) Аксиомы статики. Задачи статики. Принцип освобождения от связей.
Статика- раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов
1) если на твердое тело действуют две силы то тело, может находиться в равновесии, когда силы противонаправлены и лежат на одной прямой.
2) действие данной системы сил не измениться, если к ней добавить (отнять) уравновешенную систему сил.
3) две силы приложенной в одной точке можно заменить одной силой (равнодействующей).
4) силы, с которыми 2 тела действуют друг на друга = по модулю но противоположны по направлению
5)равновесие деформируемого тела не нарушиться, если тело считать затвердевшим (абс твердым)
Две основные задачи статики.
1. Задача о приведении системы сил: заключается в замене данной системы сил другой, наиболее простой, ей эквивалентной.
2. Задача о равновесии состоит в определении условий, при которых система сил, приложенная к телу будет уравновешенной системой.
Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей.
2) Основные связи и их реакции. Проекция сил на ось и на плоскость.
1. Гладкая плоскость (поверхность) или опора: Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке.
2. Гибкая нить (провода, канаты, цепи, ремни): Реакция Т направлена вдоль нити к точке подвеса.
3. Невесомый стержень с шарнирами: Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция N изображается от тела по стержню, в предположении, что в равновесии стержень растянут.
4. Неподвижный цилиндрический шарнир или подшипник: Реакция RA цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскости Аху. Обычно ее раскладывают на две составляющие ХА и YA по двум взаимноперпендикулярным направлениям.
5. Шарнирно-подвижная опора (опора на катках): Реакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости.
6. Жесткая заделка: Нахождение реакции жесткой заделки сводится к определению составляющих ХА и YA препятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента mA, препятствующего вращению балки под действием приложенных к ней сил.
Проекция силы на ось – алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Проекция Fx силы на ось х положительна, если угол α острый, отрицательна - если угол α тупой. Если сила перпендикулярна оси, то ее проекция на ось равна нулю.
Проекция силы на плоскость Оху – вектор, заключенный между проекциями начала и конца силы на эту плоскость. Т.е. проекция силы на плоскость величина векторная, характеризуется не только числовым значением, но и направлением в плоскости Оху (рис.1.12).
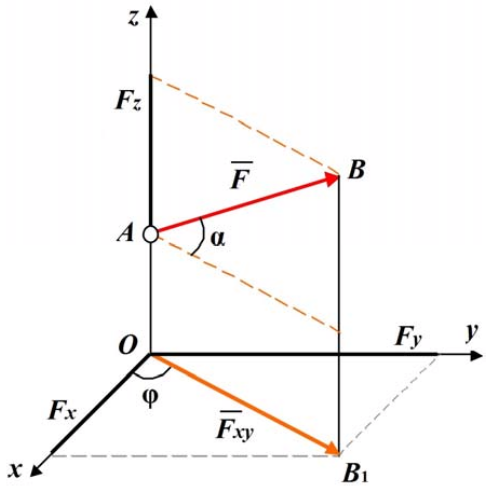 Тогда модуль проекции на плоскость Оху будет равен: Fxy = F cosα, где α - угол между направлением силы и ее проекцией.
Тогда модуль проекции на плоскость Оху будет равен: Fxy = F cosα, где α - угол между направлением силы и ее проекцией.
Если сила и ось координат не лежат в одной плоскости, то проекция силы на ось проводится методом двойного проецирования.
Например, чтобы определить проекцию силы на ось х, надо спроецировать ее на плоскость Оху, а затем разложить проекцию силы на составляющие по осям координат Fx и Fy (рис. 1.12).
Fx = Fxy cosφ = F cosα cosφ; Fy = Fxy sinφ = F cosα sinφ; Fz = F sinα.
3) Аналитический и геометрический способ задания силы и аналитический и геометрический способ сложения сил
Система сил, линии действия которых лежат в одной плоскости называется плоской.
Геометрический способ сложения сил. Геометрическая сумма (главный вектор) системы сил F1, F2, ..., Fn определяется построением силового многоугольника. Для этого пользуются правилом сложения векторов. В произвольной точке О вектор R, соединяющий начало первого вектора F1 с концом последнего Fn изображает геометрическую сумму или главный вектор слагаемых сил:
R = F1 + F2 + ... + Fn = SFk. (k = 1, 2, .., n)








