Элементарная Работа потенциальной силы.
В потенциальном силовом поле Элементарная Работа силы равна полному дифференциалу потенциала , Fdr = dU . Покажем это.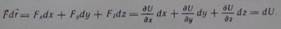 
Нахождение потенциала силы.
1) Сначала нужно выяснить, потенциально ли рассматриваю сила. Для этого можно воспользоваться критерии потенциальности rot F =0, который в декартовых координатах имеет вид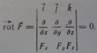 
2) Получим полный дифференциал потенциала, используя 
3)Проинтегрировать это выражение
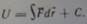
Постоянную C положить равной нулю, это определит точки поля, в которых потенциал равен нулю. 
23. Физический смысл потенциала. Потенциальная энергия точки в точке поля. Консервативная система точек. Механическая энергия материальной точки и системы точек.
1) Физический смысл потенциала
Работа на пути между точками 1 и 2.
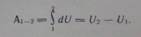
Работа потенциальной силы на пути между двумя точками поля равна разности потенциалов конечной и начальной точках поля.
2) Потенциальная энергия материальной точки в потенциальном силовом поле.
Чтобы в данную точку Поля с потенциалом U поместить из «бесконечности» материальную точку, на которую действует сила поля, необходимо совершить работу против силы поля, то есть равную - U. В результате материальной точки, находящейся в потенциальном силовом поле, обладает такой энергии, эта энергия называется потенциальной энергии. Потенциальная энергия материальной точки в потенциальном силовом поле численно равна потенциал поля со знаком «минус», П= - U.Гравитационном поле, создаваемым массой m0, материальная точка массы m, находящийся на расстоянии r от m, обладает социальный энергией
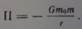
В электрическом кулоновском поле, создаваемом положительным зарядом +e0, материальная точка, несущая отрицательный заряд –e и находящаяся настроение на расстоянии r от e0, обладает потенциальной энергии
Потенциальная энергия материальной точки массы m в однородном поле силы тяжести зависит от высоты и равна
3) Механическая энергия материальной точки
Материальная точка, движущиеся в потенциальном силовом поле, обладает кинетической и потенциальной энергией.
Сумма кинетической и потенциальной энергии точки называется механической энергией точки
4) Механическая энергия системы точек.
24. Закон сохранения механической энергии точки и системы точек.
