Второй закон Ньютона: Основной закон механики.
Он устанавливает количественную связь между силой, действующей на материальную точку, и вызываемым этой силой изменением движения точки. Отвечает на вопрос, как движется материальная точка в инерциальной системе отсчета, если на точку действуют силы: Изменение импульса материальной точки за единицу времени пропорционально приложенной силе и происходит в направление действия этой сил.
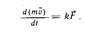
В этом законе коэффициент k определяется выбором единиц измерения. Так как второй закон служит определяющим уравнением для единицы массы или силы, то k = 1, и тогда второй закон принимает вид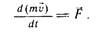 
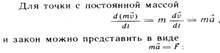
В любой момент времени для движущейся в инерциальной системе отчета материальной точки, произведение массы этой точки на ее вектор ускорения численно равно вектору силы, действующей на точку.
Второй закон Ньютона имеет универсальный характер: он справедлив для материальной точки в любой инерциальной системе отсчета и в любой момент времени.
Он является основным законом механики, так как объединяет кинематику (через ускорение) и динамику (через массу и силу). Он позволяет описать любое движение материальной точки в дифференциальных уравнениях (позволяет решать основную задачу механики).
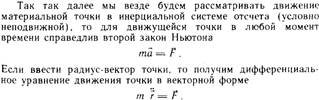
10. Первая и вторая задачи динамики.
Первая задача динамики: Определение силы по заданному движению.
Вторая задача динамики: Определение движения по заданным силам (основная задача механики).
11. Основная задача механики для точки и системы точек. Общий путь ее решения.
Вторая задача динамики: Определение движения по заданным силам (основная задача механики).
Общий путь решения основной задачи механики :
12. Примеры решения основной задачи механики для прямолинейного движения материальной точки, в том числе для линейного осциллятора.
1. Условие прямолинейности движения точки:
2. Случай постоянной силы:
3. Случай силы, зависящей от скорости движения точки:
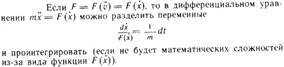
4. Случай силы, зависящей от положения точки:
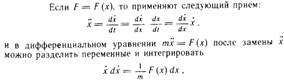
13. Решение основной задачи механики для криволинейного движения точки под действием постоянной силы.
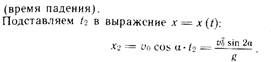
14. Решение основной задачи механики для центрально-симметрического поля: центральные силы, дифференциальные уравнения движения, интеграл площадей, второй закон Кеплера.
1. Определение центральной силы:
2. Движение точки под действием центральной силы всегда плоское :
3. Движения точки под действием центральной силы:
15. Решение основной задачи механики для центрально - симметрического поля: формула Бинэ, траектория точки для случая силы F = - l / r 2
1. Формула Бинэ:
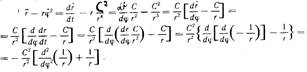
2. Траектория точки для случая силы F = - l / r 2
16. Определение величин, характеризующих движение и действия сил.
1. Определение величин характеризующих движение:
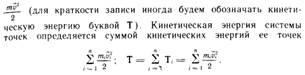
2. Определение величин характеризующих действия сил:
17. Закон изменения импульса и закон сохранения импульса.
1. Закон изменения импульса:
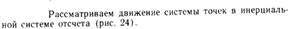
2. Закон сохранения импульса:
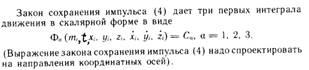
18. Центр масс системы точек. Положение центра масс. Теорема о движении центра масс системы точек.
1. Центр масс системы точек:
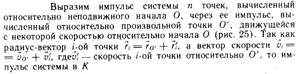
2. Положение центра масс:
3. Теорема о движении центра масс системы точек:
19. Закон изменения момента импульса и закон сохранения момента импульса.
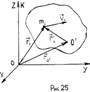
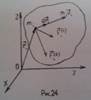
1. Закон изменения момента импульса
Для каждой точки системы точек, движущееся под действием внешних и внутренних сил (рисунок 24), Запишем Второй закон Ньютона и умножить обе части слева на радиус вектора r
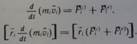
Левую часть можно изменить произвольно по времени и момента импульса i-ой точки:
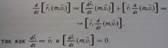
Сложим почленно полученное выражение, будем иметь
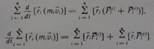
Так и главный момент внутренних сил равен нулю, то
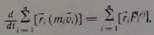
Или для кратности записи
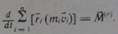
Это Закон изменения момента импульса: Производная по времени от момента импульса системы точек, вычисленного в инерциальной системе отсчета, численно равно главному моменту внешних сил, действующих на точке системы, или изменение момента импульса системы точек за единицу времени равна главному момента внешних сил, действующих на точки системы.
Можно показать, что теорема об изменении момента импульса системы точек справедлива и относительно центра масс системы.
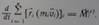
Для одной точки закон об изменении момента импульса имеет вид: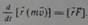 
Производная по времени от момента импульса точки, вычисленного относительно некоторого начала, равна моменту силы, действующей на точку, относительно того же начала. Закон изменения момента импульса может быть записана в виде трех скалярных выражения, представляющих его проекции на координатные оси, которые удобно получить, используя представления векторного произведения через определитель 3 порядка.
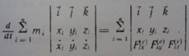
2. Закон сохранения момента импульса
Если главный момент внешних сил равен нулю, то момент импульса системы точек остается постоянным:
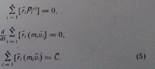
Закон сохранения момента импульса имеет место в следующих случаях.
Наибольший интерес представляет случай центральных сил.
Закон сохранения момента импульса (5) проекциях на направление координатных осей дает 3 скалярных поражений, которые представляют собой первые интегралы движения.
Их легко получить, используя для (5) выражение
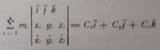
На практике можно иметь место сохранения момента импульса системы точек, в некотором направлении, если проекция главного момента внешних сил на это направление равна нулю.
20. Вращение твердого тела вокруг неподвижной оси. Вывод дифференциальных уравнений движения математического и физического маятника.
Применим закон об изменении момента импульса вращения твердого тела вокруг неподвижной оси (рис. 26)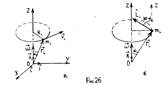 
21. Закон изменения кинетической энергии для материальной точки и системы материальных точек в дифференциальном и интегральном виде. Теорема Кёнига.
Закон изменения кинетической энергии для материальной точки.
Запиши Второй закон Ньютона для материальной точки.
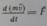
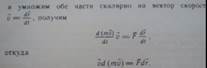Для постоянной массы это выражения можно записать в виде 
Это Закон изменения кинетической энергии для точки в дифференциальной форме: Дифференциал кинетической энергии точки равен элементарной работы сил, действующих на точку, или изменении кинетической энергии точки за бесконечно малый промежуток времени равно элементарной работы сил, действующих на точку.
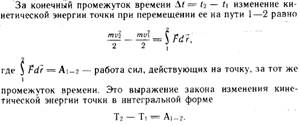
22. Потенциальное силовое поле. Условие потенциальности. Элементарная работа потенциальной силы. Нахождение потенциальной силы. Примеры потенциальных сил: гравитация, сила тяжести, кулоновская, упругая. Примеры потенциальных полей.
Потенциальное силовое поле.
Если в каждой точке поля сила может быть представлена как Градиент некоторые скалярной функции U=U(r) F=grad U
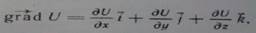То сила и ее поле называются потенциальными, а функция U(r) - потенциальной функцией поля, или потенциалом поля, а также потенциалом силы в декартовой системе координат, а силу можно представить в виде
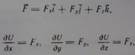
То есть в каждой точке силового потенциального поля проекция силы на координатную ось равна частные производные от потенциала по соответствующей координате.