Движение задается траекторией точки.

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

ρ =ρ(t)-радиус кривизны.

, ,

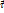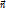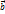
Изменение радиус-вектора:

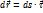
Вектор скорости: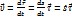

Вектор ускорения: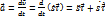

Модуль вектора ускорения: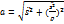

Проекция вектора ускорения на бинормаль всегда равна нулю, ускорение лежит в соприкасающейся плоскости.

4. Задание движения твердого тела, кинематические характеристики вращательного движения тела и точек тела (формула Эйлера, ускорение точек).

1. Задание движения свободного твердого тела и его точек.

Задача механики – уметь определять в любой момент времени в заданной системе отсчета положение каждой точки тела если задано движение тела относительно этой системы отсчета.

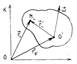
Движение твердого тела относительно неподвижной системы отсчета К нужно разложить на поступательное движение со скоростью, произвольной точки О', и вращательное движение с некоторой мгновенной угловой скоростью вокруг точки О', т.е. задать движение тела двумя векторными уравнениями.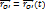

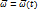
Тогда движение любой точки M_i описывается: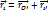

2. Частный случай движения твердого тела.

А) Поступательное движение. 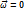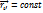. Тогда движение любой точки M_i: 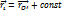. Движение твердого тела: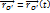

Б) Вращение тела вокруг неподвижной точки.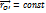

В этом случае удобно совместить начало отсчета с точкой О'. Тогда, 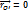. Движение любой точки M_i: 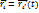. Движение твердого тела: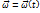

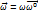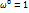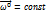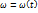В) Вращение вокруг неподвижной оси. , – орт , - задает движение тела. Любая M_i: 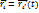, считая О' началом отсчета.

3. Кинематические характеристики вращательного движения тела вокруг неподвижной оси.

А) Угол поворота (угол собственного вращения).

Определяет положение тела в любой момент времени, т.е. является функцией времени φ=φ(t).

Б) Угловая скорость. 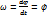. Направление : вдоль оси вращения так, что с его конца вращение тела наблюдается против часовой стрелки.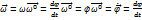

В) Угловое ускорение.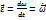

1. Равнопеременное вращение. 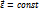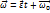. Тогда: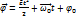

1. Равномерное вращение. 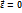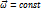. Тогда: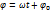

4. Выражение кинематических характеристик точек твердого тела, вращающегося относительно неподвижной оси.

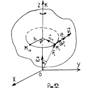
Каждая точка M_i тела описывает окружность радиусом h_i в плоскости, перпендикулярной оси вращения. Движение тела задается углом поворота φ=φ(t).

Положение точки M_i: :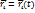

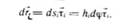
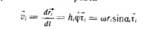
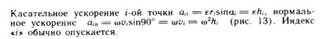
5. Выражение кинематических характеристик точек твердого тела при вращении тела вокруг неподвижной точки и в общем случае движение тела. 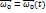– орт (задает направление) 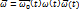–для вращения тела вокруг неподвижной точки. В общем случае, мгновенные скорости и ускорения имеют вид: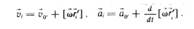

Формулы Пуассона:

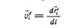
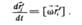
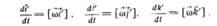
Производная по времени от вращающегося с угловой скоростью единичного вектора равна вектору векторного произведения вектора угловой скорости и самого единичного вектора.

5. Абсолютное, относительное и переносное движение точки. Теорема о сложении скоростей.