1. Предмет, объект и основные понятия классической механики.
Механика как раздел физики изучает наиболее простую из всех форм движения материи – механическое движение. Механическое движение – изменение положения тела в пространстве и во времени.
Объекты изучения классической механики:
1. Материальная точка – точка, обладающая определенной массой.
2. Система материальных точек – совокупность тел, размерами которых можно пренебречь.
3. Особенная система материальных точек – твердое тело – тело с неизменяющимися размером и формой (не подверженное деформации).
Пространство и время – форма существования материи. В классической механике абсолютное пространство и абсолютное время.
Свойства абсолютного пространства:
1. Бесконечность
2. Однородность (свойства пространства одинаковы во всех его точках)
3. Непрерывность
4. Многонаправленность
5. Изотропность – все направления в пространстве равноправны.
Свойства абсолютного времени:
1. Бесконечность
2. Однородность (позволяет установить одновременность событий; время течет одинаково во всех точках пространства)
3. Непрерывность
4. Однонаправленность.
Обнаружить перемещение тел в однородном и изотропном пространстве невозможно, поэтому необходимо рассматривать движение относительного какого-либо другого тела – тела отсчета. Для того, что бы замечать движение тела относительно тела отсчета, его связывают с некоторой системой координат. Тогда положение точки будет определяться определенными координатами. Для определения положения тела во времени вводят способ фиксации времени.
Тело отсчета, связанная с ним система координат и часы образуют систему отсчета относительно которой рассматривается механическое движение тел. Законы движения в разных система отсчета имеют разный вид. Желательно использовать такие система отсчета, в которых законы выглядят наиболее просто. Такие системы называют инерциальными (ИСО). Частный случай ИСО – абсолютно неподвижная система отсчета.
Разделы классической механики:
1) Кинематика – изучает движение, без причин его вызывающих (геометрически)
2) Динамика – изучает движение с учетом взаимодействия между телами. Частным случаем динамики является статика – изучает равновесие тел.
2. Способы задания движения (векторный, координатный, естественный). Связь между разными способами движения точки.
1. Векторный способ задания движения.
Положение точки определяется радиус-вектором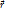 
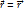(t)
Траектория точки представляет собой геометрическое место концов радиус-вектора точки.
Направление 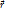можно задать единичным вектором(ортом) 
.
= 
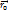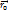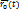
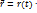
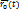
Вектор элементарного перемещения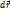 
(изменение вектора 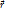за бесконечно малый промежуток времени dt) находится как дифференциал векторной функции 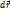= dr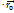 
+ 
.
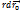2. Естественный способ задания движения.
Задается траектория движения точки аналитически или геометрически. На ней отмечается точка отсчета. Положение движущейся точки определяется расстоянием s = s(t) до нее от точки О отсчитываемым по траектории.
Расстояние s не дает информации о траектории, но ее можно задать, например, радиусом кривизны ρ =ρ(t) (ρ = ∞ - прямая; ρ = R – окружность). При естественном способе задания движения с каждой точкой можно связать прямоугольную систему координат, определяемую единичными векторами, направленными по: 1. Касательной (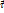 
); 2. Главной нормали ( 
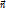); 3. Бинормали (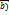 
естественный трехгранник.
Ос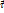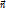и , и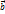 
образуют правую тройку векторов. За положительное направление отсчета расстояния по траектории от точки О принимается направление 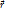. Плоскость, в которой лежат касательная и нормаль называют соприкасающейся плоскостью.
3. Координатный – движение задается координатами, которые являются функциями времени и называются уравнениями движения точки.
1) Декартова: x = x(t); y = y(t); z = z(t).
2) Полярная:
r = r(t)
φ = φ(t)
OX – полярная ось
О – полюс
r = OM – расстояние от точки М до полюса
φ – полярный угол точки М.
Так как движение точки непрерывно, то все функции которые оно задает должны быть непрерывными, однозначными и дважды дифференцируемыми.
4. Связь между различными способами задания движения.
1. В декартовой системе:
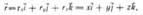
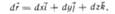
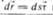
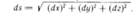
s =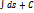 
, где С определяется начальными условиями.
В полярной системе координат:
r = r(t)
φ = φ (t)
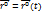– орт радиального направления
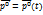- орт поперечного направления
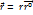
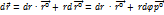
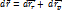
3. Кинематические характеристики точки (радиус-вектор, вектор скорости, вектор ускорения), их выражения при разных способах задания движения.
Абсолютное движение – движение относительно неподвижной (или условно неподвижной) системы отсчета (т.е. ИСО). Величины, полностью описывающие движение геометрически – кинематические характеристики ( радиус-вектор, вектор скорости, вектор ускорения).
1. Векторный способ задания движения.
Радиус-вектор – это величина, характеризующая положение точки в любой момент времени ( функция времени). 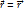(t)
Вектор скорости – это физическая величина, характеризующая изменение положения движения точки через изменения ее радиус-вектора (за единицу времени).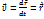 
Вектор ускорения – физическая величина, характеризующая изменение вектора скорости.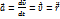 
2. Координатный способ.
А) Декартова система координат.
x = x(t)
y = y(t) - уравнения движения
z = z(t)
Радиус-вектор: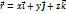 
Вектор скорости: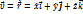 
Проекции вектора скорости: 
Модуль вектора скорости: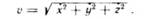 
Вектор ускорения: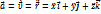 
Проекции вектора ускорения: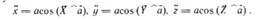 
Модуль вектора ускорения: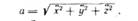 
Б) Полярная система координат.
r = r(t)
φ = φ(t)
Орты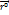 
, 
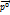
Радиус-вектор: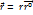
Вектор скорости:
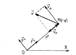
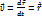
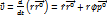
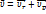
Вектор ускорения:
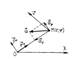
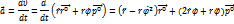
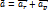
3. Естественный способ задания движения.