Техническая электродинамика

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

МИНОБРНАУКИ РОССИИ

–––––––––––––––––––––––––––––––––

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

–––––––––––––––––––––––––––––––––––––––

И. Г. Мироненко А. А. Иванов

ТЕХНИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА

Учебное пособие

Санкт-Петербург

Издательство СПбГЭТУ «ЛЭТИ»

2016

УДК 621.31(075):621.396(075)

ББК В336я7:З845-01я7

М64

Мироненко И. Г., Иванов А. А.

М64 Техническая электродинамика: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2016. 147 с.

ISBN 978-5-7629-1572-4

Предназначено для студентов, обучающихся по направлению 11.03.03 «Конструирование и технология электронных средств». Также может быть полезно инженерно-техническим работникам этой области знаний.

УДК 621.31(075):621.396(075)

ББК В336я7:З845-01я7

Рецензенты: кафедра проектирования и технологии производства электронной аппаратуры МГТУ им. Н. Э. Баумана; д-р техн. наук, проф. С. М. Ни­кулин (НГТУ им. Р. Е. Алексеева).

Публикация выполнена в рамках государственной работы «Проведение научно-исследовательских работ» (задание № 2016/187, код проекта 1031) базовой части государственного задания Минобрнауки России.

Утверждено

редакционно-издательским советом университета

в качестве учебного пособия

ISBN 978-5-7629-1572-4 © СПбГЭТУ «ЛЭТИ», 2016

1. ЛИНИИ ПЕРЕДАЧИ СВЕРХ- ВЫСОКИХ ЧАСТОТ

1.1. Прямоугольные волноводы

Устройства, канализирующие электромагнитную энергию, называют линиями передачи сверх высоких частот. Строго говоря, линия передачи - это устройство, образованное как минимум двумя проводниками. Например, коаксиальная линия. Однако, в инженерной практике к ним относят и волноводы, представляющие собой полые металлические трубы. Подробный анализ электромагнитного поля в волноводах выполнен в первой части курса "Электромагнитные поля и волны". Поэтому мы рассмотрим только основные характеристики электромагнитного поля в волноводах, наиболее значимые для расчета их основных параметров, как объектов инженерного анализа.

В волноводах могут распространяться электромагнитные волны двух видов: поперечные электрические волны, обозначаемые TE-волны и поперечные магнитные волны, обозначаемые TM-волны. В структуре ТЕ-волн отсутствует продольная компонента электрического поля, в структуре TM-волн отсутствует продольная компонента магнитного поля. В обобщенной цилиндрической системе координат (декартовой или полярной) это означает, что у TE-волн E_z=0, у TM-волн H_z=0. Поэтому TE-волны называют волнами магнитного типа или H-волнами. TM-волны называют волнами электрического типа или Е-волнами. В общем случае в структуре волн магнитного типа две поперечные компоненты электрического поля и три компоненты магнитного поля. В структуре волн электрического поля две компоненты магнитного поля и три компоненты электрического поля.

Поля в волноводах зависят от продольной координаты в явном виде, как e ^{- j g z}, где g - постоянная распространения. Зависимость полей от поперечных координат определяется соотношением размеров поперечного сечения и длины волны на рабочей частоте. В волноводах зависимость всех компонент поля от поперечных координат, определяется зависимостью продольных компонент электрического и магнитного полей от поперечных координат. В прямоугольных волноводах решениями уравнений Максвелла являются зависимости

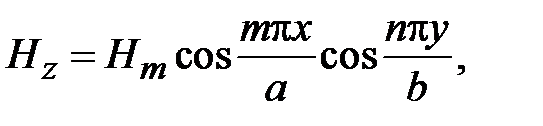
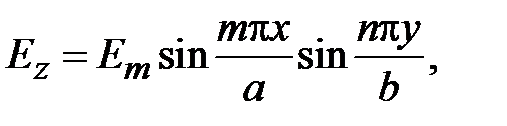
где m и n - положительные целочисленные значения 0,1,2 .., а, b – размеры широкой и узкой стенок волновода. Из уравнений Максвелла можно найти зависимости компонент E_x, E_y, H_x, H_y от поперечных координат, которые будут определяться числом полуволн синусов и косинусов по длине стенок волновода.

Произвольным парам значений m и n, соответствуют типы (моды) полей волн электрического и магнитного типа. Они обозначаются: как Н _mn (ТЕ _mn) волны, или E_mn (ТМ _mn) волны. Для каждого типа Е _mn и H_mn волн, т.е. для каждой пары значений m и n определены такие параметры, как поперечное волновое число 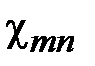, граничная частота 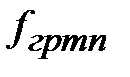и критическая длина волны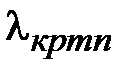

, , ,

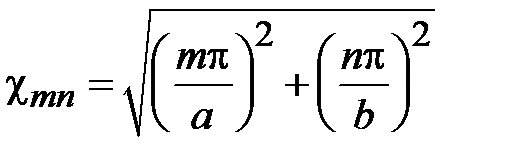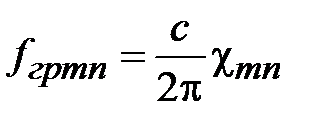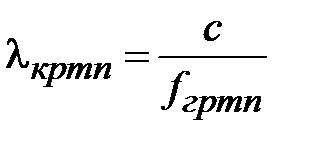где с - скорость света в свободном пространстве 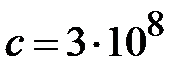м/с. Условием существования волны Н _mn или E_mn на рабочей частоте 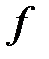является соотношение

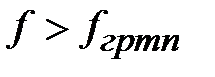или .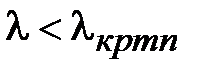

Основным типом волны в волноводе, называют волну с минимальным значением граничной частоты или максимальным значением критической длины волны. При условии, что а>b основным типом волны, является волна магнитного типа с m=1 и n=0, т.е. волна Н₁₀. Её граничная частота 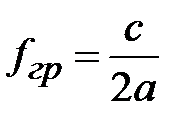, критическая длина волны 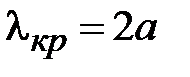. Все остальные волны электрических и магнитных типов имеют большие значения граничных частот. При 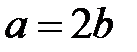, значение граничной частоты волны Н₁₁ и Е₁₁ равно 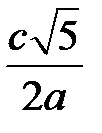. Граничные частоты для основного типа и трех ближайших высших типов волн приведены на рис. 1.1.

Штрихованная область обозначает рабочую полосу частот одномодового режима волновода с волной Н₁₀.

Зависимости компонент поля Н₁₀ от поперечных координат имеют вид

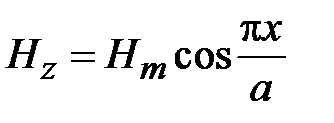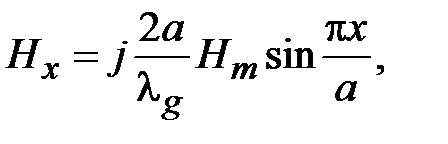
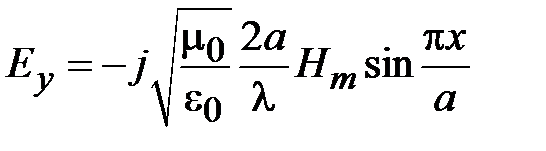, , (1.1)

где 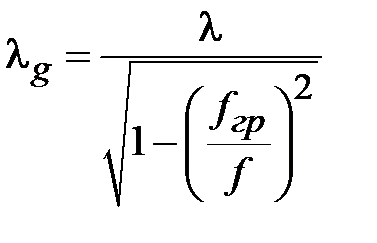- длина волны в волноводе, 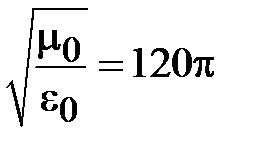- волновое сопротивление свободного пространства.

Мощность передаваемая по волноводу волной Н₁₀ определяется реальной частью потока комплексного вектора Пойнтинга через поперечное сечение волновода 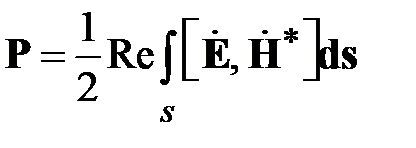. Подставив сюда соотношение (1.1) найдем соотношение для мощности переносимой волной Н₁₀

.

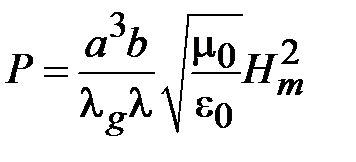Если в (1.1) положить 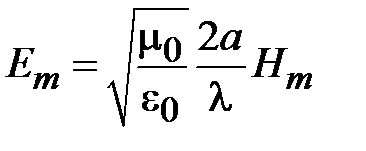, тогда

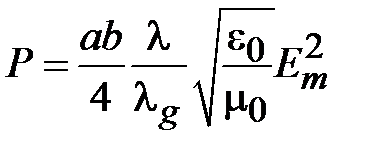. (1.2)

Из (1.2) можно найти предельное значение мощности передаваемой волной Н₁₀ исходя из пробивного значения напряженности электрического поля, которое в диапазоне сантиметровых волн близко к 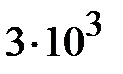В/мм. Поэтому на частоте 10 ГГц по волноводу с поперечным сечением (23х10)мм² можно передать максимальную мощность близкую к 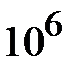Вт. Разумеется, что это предельное теоретическое значение уровня передаваемой мощности, определяемое максимальным значением пробивного напряжения.

При конечной проводимости стенок волновода в них течет электрический ток на малой глубине, называемой глубиной проникновения поля в металл стенок или толщиной скин- слоя, значение которой определяется соотношением

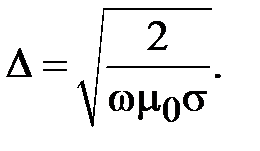(1.3)

Ток в скин- слое можно считать поверхностным током линейная плотность которого определяется соотношением

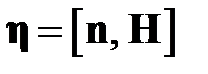, (1.4)

где 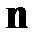- орт нормали к поверхности стенок волновода, 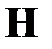- вектор напряженности магнитного поля на стенках волновода. Таким образом, по широким стенкам волновода, нормаль к которым совпадает с осью y , течет поверхностный ток, имеющий две компоненты 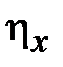и 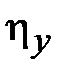равные

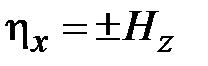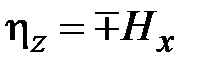, . (1.5)

Вдоль боковых стенок волновода, нормаль к которым совпадает с осью x , течёт поверхностный ток

.

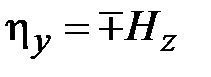Разные знаки в формулах относятся к токам на противоположных стенках волновода.

Токи в стенках волновода, приводят к затуханию электромагнитной волны, вызванному омическими потерями в стенках волновода. Коэффициент затухания волны Н₁₀ может быть вычислен по формуле

Рис. 1.2

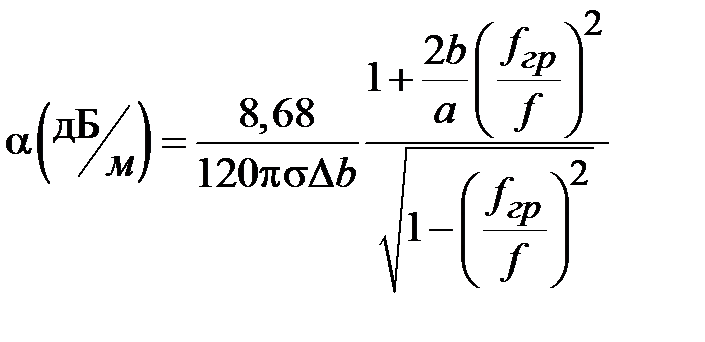. (1.6)

Зависимость коэффициента затухания 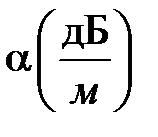от частоты в логарифмическом масштабе для медного волновода с поперечным сечением 23х10мм² приведена на рис. 1.2.

При приближении к граничной частоте затухание резко нарастает. С ростом частоты после слабо выраженного частотного минимума коэффициент затухания медленно растет с ростом частоты.

Коэффициент затухания основной волны прямоугольного волновода Н₁₀ имеет минимальное значение среди всех типов волн. Численное значение коэффициента затухания на частоте 10¹⁰ Гц близко 0.12 дБ/м, что приводит к спаду мощности в два раза на длине примерно 25м.

1.2. Круглые волноводы

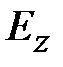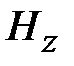В круглых волноводах внутреннего радиуса а, зависимость продольных составляющих и волн электрического и магнитного типов и определяются одинаковыми соотношениями

,

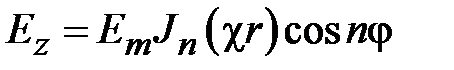(1.9)

,

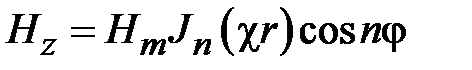где 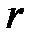и 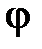- полярные координаты на поперечном сечении волновода.

Различие волн возникает при наложении граничных условий на 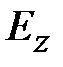и .

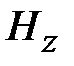Рассмотрим волны электрического типа. Продольная составляющая электрического поля обращается в ноль на поверхности волновода в случае идеально проводящего металла, 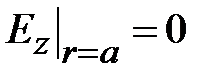что в соответствии с (1.9) приводит к уравнению относительно поперечного волнового числа

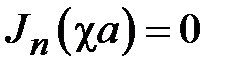. (1.10)

Это уравнение имеет бесконечное число решений, которые можно пронумеровать как m=1,2 ... и представить их в виде

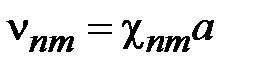, (1.11)

где 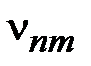- корень решение уравнения (1.10) для функций Бесселя n- го порядка.

Основной волной электрического типа в круглом волноводе является волна с минимальным значением корня 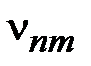. Его значение равно первому нулю функции Бесселя нулевого порядка 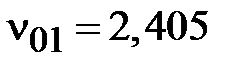. Таким образом, для волны Е₀₁ граничная частота в соответствии с определением и соотношением (1.11) равна

.

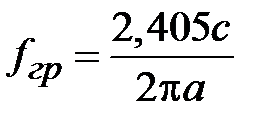Структура поля волны Е₀₁ на поперечном сечении волновода определяется соотношениями

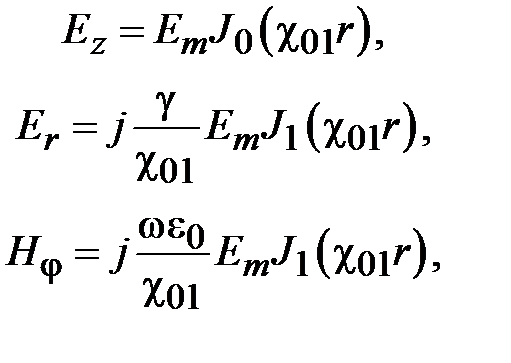
где .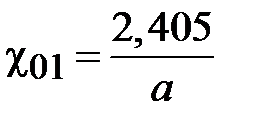

Как видно из приведенных соотношений волна Е₀₁ не зависит от угла j и, следовательно, обладает угловой симметрией. Силовые линии электрического поля волны ориентированы на поперечном сечении по радиусу. Силовые линии магнитного поля представляют собой окружности, охватывающие силовые линии электрического поля.

Рассмотрим волны магнитного типа. Продольная составляющая магнитного поля 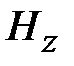удовлетворяет граничному условию в виде обращения в ноль производной по нормали к поверхности идеально проводящего металла. Для круглого волновода это означает, что в соответствии с (1.9) должно быть выполнено условие

.

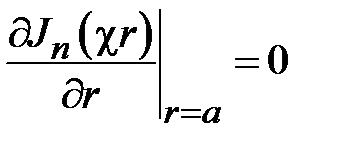Обозначим корни этого уравнения как 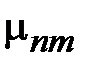где m - номер корня в бесконечной последовательности корней уравнения. Минимальное значение имеет первый корень при n=1, который отвечает основной волне Н₁₁, поэтому 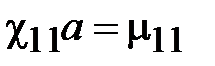, где . Таким образом, граничная частота поля Н₁₁ равна

.

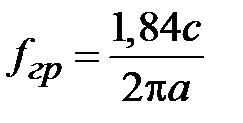Как видно, граничная частота поля Н₁₁ меньше граничной частоты поля Е₀₁. Поэтому основной волной среди волн электрических и магнитных типов является волна Н₁₁. Зависимость компонент поля волны Н₁₁ от поперечных координат имеет вид

,

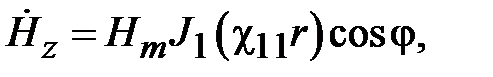
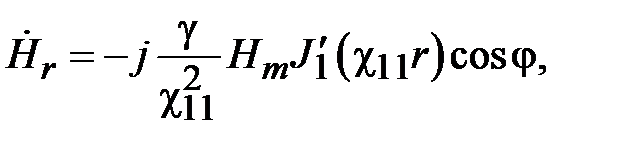
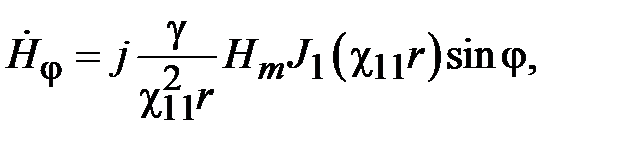
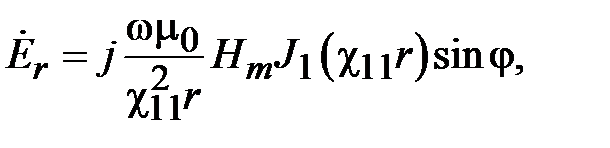
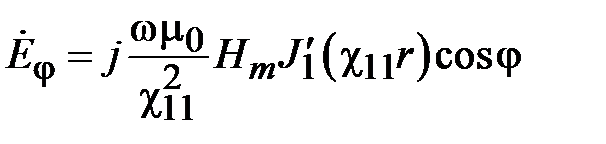где , .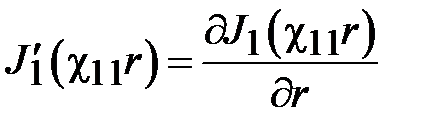

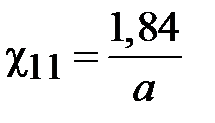Угловая зависимость компонент поля определяется углом j, отсчет которого в полярной системе координат может быть произвольным. Однако, пространственное положение максимального значения напряженности магнитного поля определяет поляризацию волны. Волна Н₁₁ может изменить поляризацию вследствие изгибов или неровностей внутренней поверхности трубы, поэтому круглые волноводы редко применяются для передачи СВЧ мощности.

1.3. Прямоугольные волноводы сложного поперечного сечения

Прямоугольный волновод с волной Н₁₀, является основным устройством для передачи электромагнитной энергии. Полоса рабочих частот волновода рис. 1.1., лежит между значениями нижней частоты ( 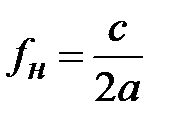), и значением верхней частоты ( 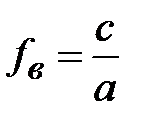). Таким образом, рабочий диапазон частот одномодового режима определяется как 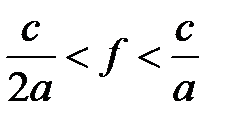. Однако в технике сверх- высоких частот часто возникает необходимость расширения рабочей полосы частот. Этому требованию отвечают волноводы Н и П - образной формы поперечного сечения, рис.1.3.

Такие волноводы относят к волноводам со сложным поперечным сечением. Строгий электродинамический анализ таких волноводов сложен и не приводит к простым соотношениям для расчета граничной частоты, распределения поля, затухания и других характеристик в отличие от волноводов прямоугольной формы сечения. Однако, в конструкции Н и П образных волноводов, заложены инженерные идеи, которые можно пояснить. Во первых, заметим, что П образный волновод, является симметричной половиной Н образного волновода, и поэтому, суждение о Н волноводе в равной степени относится и П волноводу.

Ограничение полосы частот в прямоугольном волноводе вызвано наличием вертикальных стенок. При формальном устремлении ширины широкой стенки волновода к бесконечности, волновод преобразуется в две параллельные металлические плоскости с основной волной ТЕМ типа с f _гр=0. Поэтому, удаление вертикальных стенок в Н волноводе от области передачи энергии приводит к уменьшению граничной частоты по сравнению с прямоугольным волноводом близких размеров. Поле основной волны в Н волноводе локализовано в его центральной части рис. 1.4. Поэтому вертикальные стенки оказывают относительно малое влияние на волновой процесс. Структура поля ближайшего высшего типа незначительно отличается от волны Н₂₀ прямоугольного волновода, что сохраняет ограничение по верхнему значению частоты в Н волноводе. Очевидно, что в Н волноводе поле основного типа зависит от оси ординат. Поэтому значение f _гр должно зависеть от высоты волновода. Изложенные качественные суждения о поле основного типа в Н волноводе, находят свое количественное выражение в приближенном соотношении для граничной частоты в виде

.

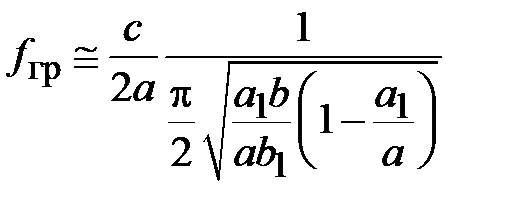Пр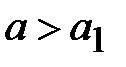и и 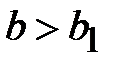можно обеспечить значение граничной частоты основной волны Н - волновода меньшее граничной частоты прямоугольного волновода при близких размерах поперечных сечений. Для этого надо выбрать размеры поперечного сечения Н - волновода так, чтобы

.

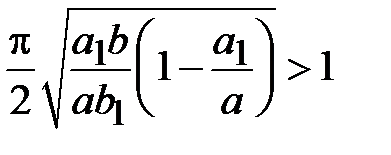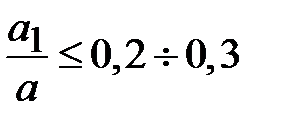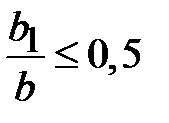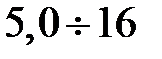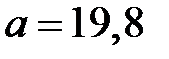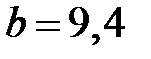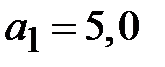На практике значения отношений , . Например, в частотном диапазоне ( )ГГц, рекомендован Н образный волновод с размерами мм, , мм, 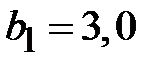мм. Для этих размеров граничная частота 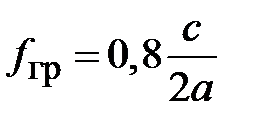. Расширение рабочей полосы частот приводит к неизбежному снижению передаваемой мощности и возрастанию затухания.

1.4. Коаксиальные линии

Рис. 1. 5

Коаксиальная линия представляет собой два соосных металлических цилиндра рис. 1.5, разделенных либо воздушным промежутком, либо диэлектриком. Этим конструкциям отвечает жесткая коаксиальная линия, либо коаксиальный кабель. В качестве диэлектрика в кабеле используются полимерные материалы с относительной диэлектрической проницаемостью 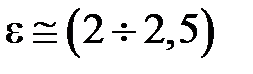. Принципиальное отличие коаксиальных линий от волноводов состоит в том, что в них основным типом волны является поперечная волна ТЕМ с f _гр=0. Очевидно, что наличие двух изолированных проводников в структуре линии, позволяет передавать постоянный ток. Верхнее значение рабочей частоты линии ограничено появлением волны ближайшего высшего типа, которой является волна Н₁₁. Ее граничная частота равна 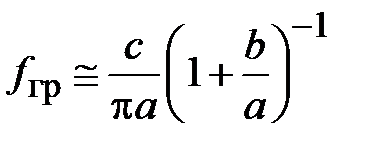, и таким образом полоса частот одномодового режима коаксиальной линии ограничена значением f _гр.

Электромагнитное поле коаксиальной линии на поперечном сечении имеет квазистатический характер. Поэтому магнитное поле коаксиальной линии идентично полю линейного постоянного тока. Обозначим 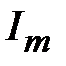- амплитуду тока в центральном проводнике коаксиальной линии и запишем магнитное поле в виде

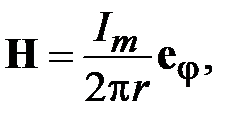
где r – координата на поперечном сечении.

Напряженность электрического и магнитного поля в ТЕМ волне связаны между собой соотношением

,

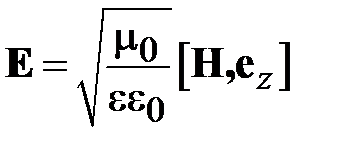откуда следует, что

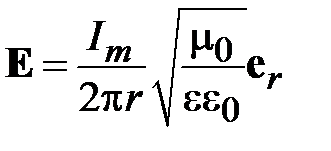. (1.12)

В силу потенциального характера поля в ТЕМ волне амплитуду напряжения между проводниками коаксиальной линии можно найти интегрированием напряженности поля (1.12) по радиусу

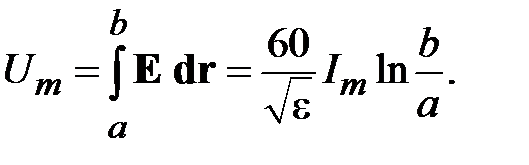(1.13)

Отношение амплитуды напряжения к амплитуде тока называется волновым сопротивлением линии

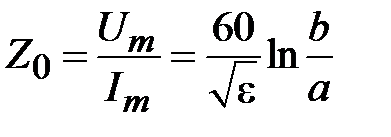. (1.14)

Для коаксиальных линий, как и волноводов, важны такие характеристики как полоса рабочих частот, максимальная передаваемая мощность и затухание.

Мощность, передаваемую по коаксиальной линии, найдем интегрированием комплексного вектора Пойнтинга по поперечному сечению

,

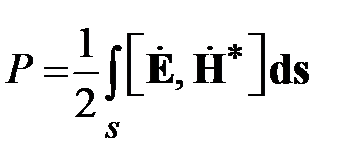где 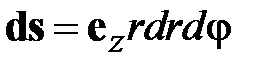- элемент интегрирования в полярной системе координат. Подставим сюда напряженности полей, получим

.

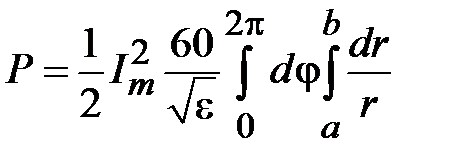Откуда следует, что

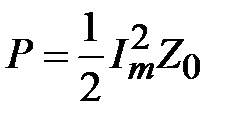. (1.15)

На основании (1.14) и (1.15) получим

.

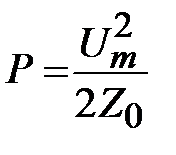Из (1.15) следует, что в соответствии с законом Джоуля-Ленца волновое сопротивление линии является нагрузкой для источника поля, подключенного к линии.

С помощью соотношение (1.13) и (1.12) можно связать значения амплитуды напряжения 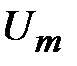с напряженностью электрического поля. Из (1.12) следует, что максимальная напряженность поля возникает на поверхности внутреннего проводника, 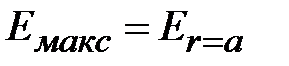. Поэтому в соответствии с (1.15) и (1.13) найдем, максимальную мощность, передаваемую по линии

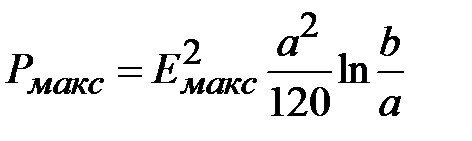. (1.16)

Из (1.16) следует, что максимальная передаваемая мощность зависит от размеров поперечного сечения. Приравняем нулю производную от передаваемой мощности (1.16) по переменной а, и при фиксированном значении b . Из уравнения 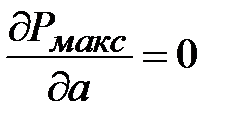найдем, что 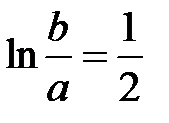или 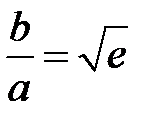. Это соответствует волновому сопротивлению линии равному 30 Ом. Для этого случая, принимая, что максимальное пробивное напряжение 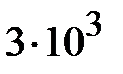В/мм найдем оценку максимальной передаваемой мощности

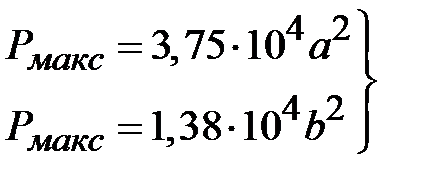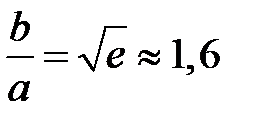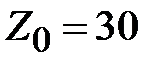при , Ом.

Коэффициент затухания электромагнитного поля в коаксиальной линии, вызванный конечной проводимостью металла, определяется соотношением

.

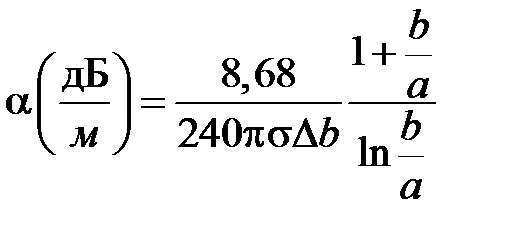Как видно, коэффициент затухания зависит от соотношения радиусов. При фиксированном значении b можно найти значение b / a, отвечающее минимуму затухания в линии. Обозначим 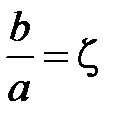и найдем условие минимума a

.

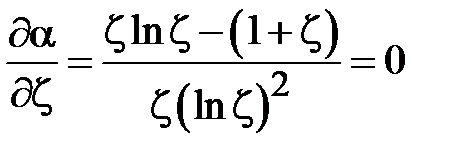Отсюда следует уравнение для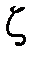

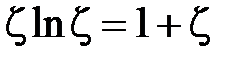
которое имеет решение 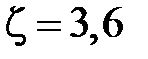. Это отношение радиусов соответствует волновому сопротивлению коаксиальной линии равному 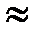77 Ом. Таким образом, минимальное затухание в коаксиальной линии определяется соотношениями

,

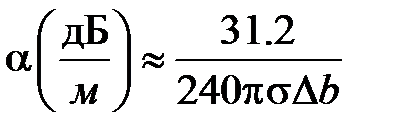при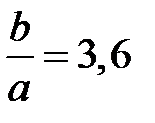

.

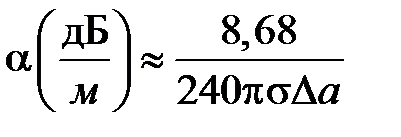С увеличением частоты затухание в коаксиальной линии монотонно возрастает и при сравнимых значениях высоты прямоугольного волновода и диаметра внутреннего цилиндра затухание в линии на частоте 10ГГц примерно в 2.5 раза выше, чем в волноводе. Размеры поперечного сечения коаксиальной линии определяются не только электродинамическими характеристиками, но и механической жесткостью конструкции.

1.5. Двухпроводные линии передачи

В группу двухпроводных линий передачи можно объединить структуры, волноведущие свойства которых определяются электродами, нанесенными на поверхность диэлектрической пластины. Такие линии передачи образуют элементную базу для построения устройств в высокочастотной части СВЧ диапазона. В настоящее время используются разнообразные линии, наилучшим образом соответствующие решению конкретных задач СВЧ техники. Рассмотрим наиболее применяемые линии: несимметричную полосковую, щелевую и копланарную. Поперечные сечения этих линий представлены на рис. 1.6.

Как видно, линии передачи представляют собой открытые волноведущие структуры, что осложняет их электродинамический анализ. Основные типы волн в двухпроводных линиях имеют нулевую граничную частоту, что является признаком ТЕМ волны. Однако, диэлектрическая граница в плоскости электродов, искажает ТЕМ волну, придавая ей характер гибридной волны с продольными составляющими электрического и магнитного поля. Вместе с тем инженерная практика применения этих линий допускает их электродинамический анализ в рамках поперечной волны и, следовательно, в квазистатическом приближении. Иначе говоря, с достаточной для практики точностью, можно перейти от решения волнового уравнения к статическому уравнению Лапласа. Это позволяет считать основной тип волны в планарных линиях квази ТЕМ типом, с присущей ему нулевой граничной частотой и слабой частотной дисперсией. Современные пакеты САПР базируются на электродинамическом анализе и, следовательно, имеют более высокую точность расчета, чем в квазистатическом приближении. Тем не менее, результаты квазистатического анализа планарных линий передачи в длинно волновом диапазоне СВЧ являются полезными.

Рассмотрим квазистатическое описание двух проводных линий передачи с ТЕМ типом волны. Распределение электромагнитного поля на поперечном сечении линии в этом случае точно отвечает распределению статического поля. Это дает основание для перехода от ТЕМ поля к волнам напряжения и тока, изменяющимся во времени по гармоническому закону. Запишем уравнения Максвелла для гармонического поля в виде

,

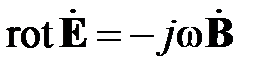(1.18)

,

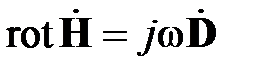где, , .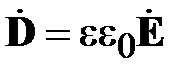

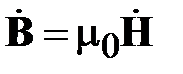Рассмотрим квазистатическое описание коаксиальной линии, а затем перенесем результаты анализа на произвольные линии, допускающие квазистатическое приближение. В ТЕМ волне коаксиальной линии напряженности электрического и магнитного полей имеют по одной составляющей. В полярной системе координат имеем

, .

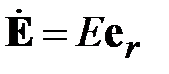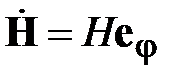Азимутальная составляющая вектора ротора в первом уравнении (1.18) равна

,

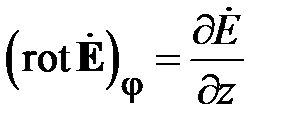и, следовательно, первое уравнение в (1.18) принимает вид

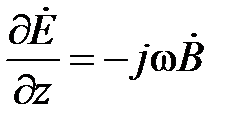. (1.19)

Проинтегрируем обе части (1.19) вдоль радиуса на поперечном сечении линии, получим

.

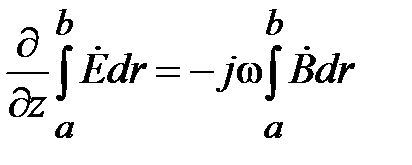В силу потенциального характера поля интеграл в левой части равен напряжению между проводниками в линии.

.

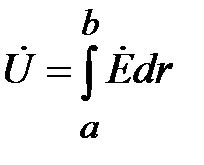Интеграл в правой части (1.19) может быть пояснен следующим образом. Поток вектора магнитной индукции в соответствии с определением равен

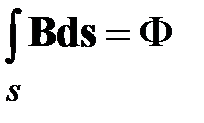. Найдем поток магнитной индукции в коаксиальной линии. Вектор магнитной индукции в коаксиальной линии имеет только одну угловую составляющую. Поэтому направление нормали к поверхности интегрирования должно совпадать с ортом 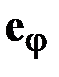, а сама поверхность ориентирована так, как показано на рис. 1.7.

Элемент поверхности равен 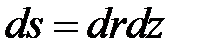, поэтому поток магнитной индукции в коаксиальной линии равен

.

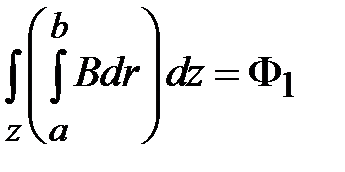Интегрирование по бесконечной длине линии означает, что внутренний интеграл равен потоку магнитной индукции приходящемуся на единицу длины линии

.

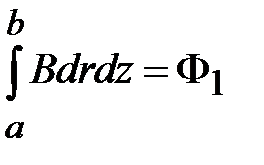По определению магнитный поток пропорционален электрическому току в проводнике. Коэффициент пропорциональности в рассматриваемом случае равен индуктивности центрального проводника, приходящейся на единицу длины – погонной индуктивности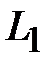

.

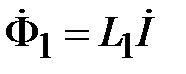Объединив полученные соотношения в уравнение, получим эквивалентную форму записи первого уравнения Максвелла в (1.18) для тока и напряжения в коаксиальной линии

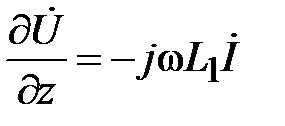. (1.20)

Радиальная составляющая вектора ротора во втором уравнении (1.18) равна

,

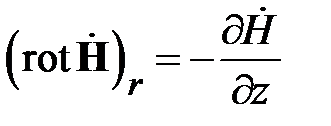поэтому из (1.18) следует, что

.

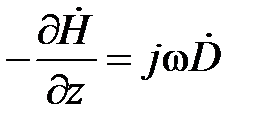Проинтегрируем полученное соотношение вдоль магнитной силовой линии, которая в коаксиальной линии представляет собой окружность. Тогда равенство преобразуется к циркуляции напряженности магнитного поля и электрической индукции

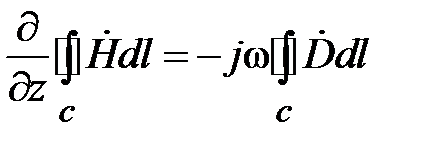. (1.21)

Интеграл в правой части (1.21) можно преобразовать к потоку индукции через замкнутую поверхность, образованную круговым цилиндром единичной длины рис.1.8.

По теореме Гаусса поток электрической индукции равен полному заряду в объеме цилиндра единичной длины, т.е. погонному заряду 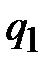. Поэтому правую часть (1.21) можно преобразовать к виду

.

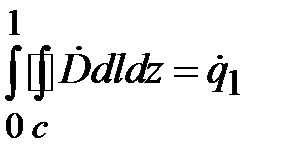Погонный заряд пропорционален напряжению между проводниками линии

,

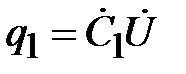где 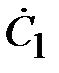- погонная емкость между проводниками линии.

Циркуляция магнитного поля в левой части (1.21) по закону Ампера равна току в линии

.

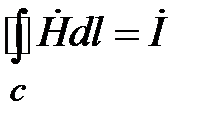Таким образом (1.21) преобразуется к виду

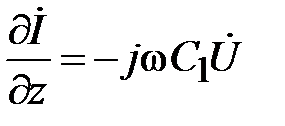. (1.22)

Уравнение (1.20) и (1.22) называются телеграфными уравнениями для гармонического напряжения и тока. Объединим (1.20) и (1.22) в систему уравнений

,

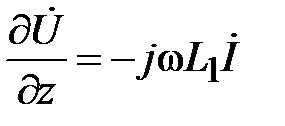(1.23)

.

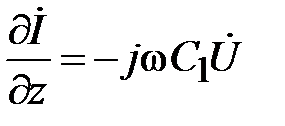Из (1.23) следуют уравнения для напряжения и тока

,

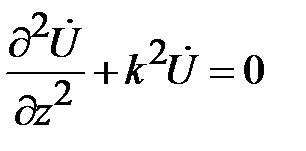(1.24)

,

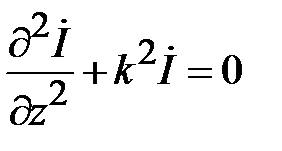где 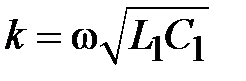- постоянная распространения.

Для определения постоянной распространения через погонные параметры линии достаточно одного из параметров, так как для ТЕМ волны 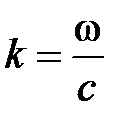. Погонная емкость может быть найдена на основе решения уравнения Лапласа в области поперечного сечения линии. Поэтому при известной погонной емкости погонная индуктивность вычисляется как 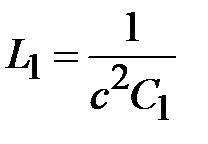. Решением уравнений (1.24) являются поперечные однородные волны. Запишем решение первого уравнения в (1.24) как сумму плоских волн распространяющихся в противоположных направлениях оси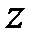

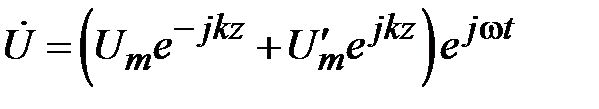. (1.25)

Тогда решение для волн тока следует из первого уравнения (1.23) в виде

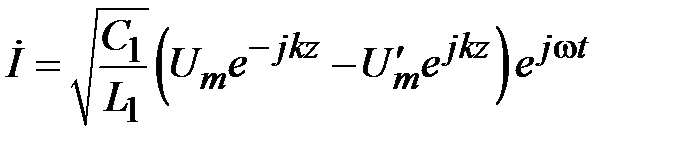. (1.26)

Отношение амплитуд напряжения и тока в прямой и обратной волне равно волновому сопротивлению коаксиальной линии. Из (1.25) и (1.26) следует, что 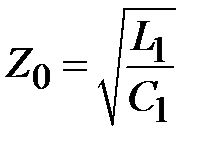. Таким образом, в линиях передачи с ТЕМ волной электромагнитное поле описывается поперечными волнами напряжения и тока, амплитуды которых пропорциональны напряженностям электрического и магнитного полей. Поэтому мощность, переносимая ТЕМ волной может быть представлена в виде 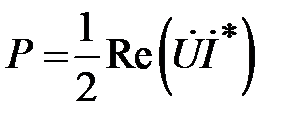, и в соответствии с (1.25) и (1.26) имеем

.

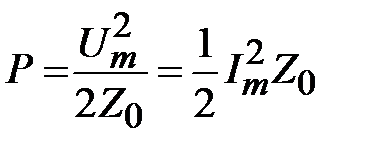1.6. Несимметричная полосковая линии

Поперечное сечение несимметричной полосковой линии приведено на рис. 1.6.а. Ее принято называть микрополосковой линией (МПЛ). Линия образована узким электродом, нанесенным на металлизированную диэлектрическую пластину с диэлектрической проницаемостью ( 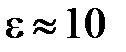). Толщина металлизации много больше толщины скин- слоя на рабочих частотах линии, но не превышает десяти микрометров. Поэтому приведенные ниже формулы получены при нулевой толщине электродов.

Волновое сопротивление МПЛ в квазистатическом приближении может быть рассчитано с точностью единиц процентов при 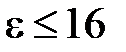по следующим формулам:

для ,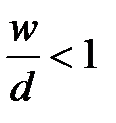

,

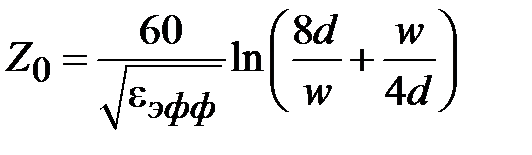где ;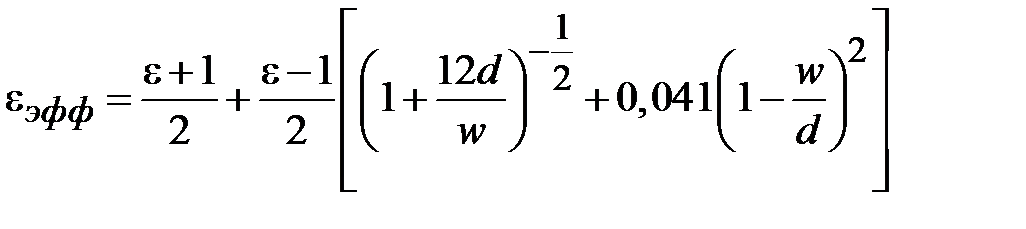

для ,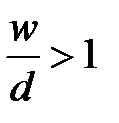

,

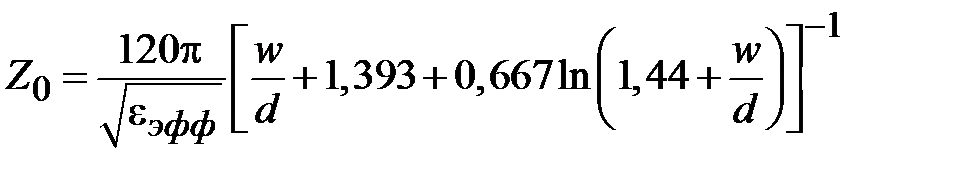где .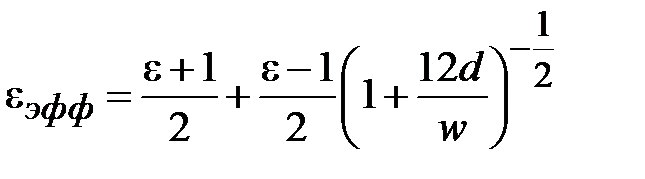

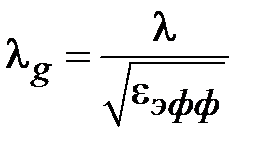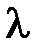Длина волны в линии равна , где - длина волны в свободном пространстве.

На рис. 1.9 приведены расчетные кривые зависимости волнового сопротивления МПЛ. Как видно пр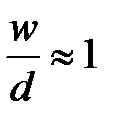и и 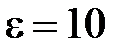, значение волнового сопротивления близко к 50 Ом. Оно согласуется с волновым сопротивлением коаксиальной линии при близких размерах поперечных сечений.

Коэффициент затухания электромагнитной волны в МПЛ, вызванный потерями в электродах, может быть рассчитан по формуле

.

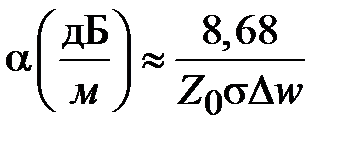Материал подложки МПЛ имеет малые диэлектрические потери оцениваемые значением 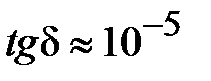на частотах (10 - 30)ГГц. Поэтому затухание в МПЛ определяется только потерями в электродах.

Максимальная рабочая частота МПЛ ограничена возбуждением волны близкой к поверхностной волне ТЕ типа. Граничная частота для МПЛ при 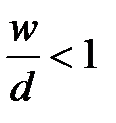может быть определена по формуле

.

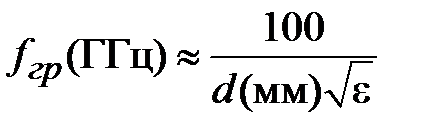Таким образом, выбор ширины полоска и толщины диэлектрической подложки является компромиссным между требуемыми параметрами волнового сопротивления, затухания и граничной частоты.

1.7. Щелевая линии

На рис. 1.6.б показано поперечное сечение щелевой линии, образованной двумя плоскими электродами, разделенными узкой щелью и нанесенными на диэлектрическую подложку. Основная волна в линии (щелевая мода) относится к гибридному типу. Локализация электромагнитного поля в области щели достигается за счет большой диэлектрической проницаемости подложки 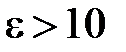и малой ширины щели 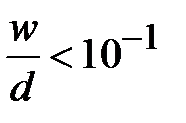. Электродинамический характер поля в щелевой линии исключает возможность определения основных параметров линии в квазистатическом приближении. Приведенные ниже графические зависимости являются результатом электродинамического анализа щелевой линии. Волновое сопротивление линии определено по мощности и напряжению между электродами

,

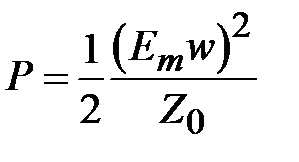где 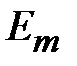- амплитуда напряженности электрического поля между электродами щелевой линии.

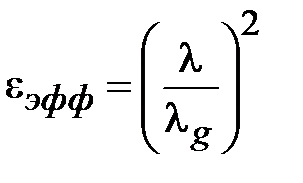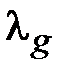Эффективная диэлектрическая проницаемость определена как , где - длина волны в щелевой линии. На рис. 1.10 и рис. 1.11 приведены графические зависимости 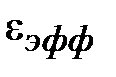, и волнового сопротивления на частоте

30ГГц, и толщине подложки d=0,5мм.

Рис. 1.10 Рис. 1.11

1.8. Копланарная линии

Копланарную линию передачи рис. 1.6.в можно считать плоским аналогом коаксиальной линии, если фазовый сдвиг между полоском линии и широкими электродами равен 180⁰. Такому состоянию потенциалов отвечает четный или синфазный тип волны. На рис. 1.12 показано распределение Электрического поля в подложке при четном типе волны. Такой тип волны устойчив при условии точной симметрии между полоском и широкими электродами. При нарушении симметрии четный тип волны может “переизлучиться” в нечетный (противофазный тип). На рис. 1.13 показано распределение электрического поля в подложке при нечетной волне. В этой волне электрическое поле “перехлестывает” центральный проводник и это приближает его к щелевой моде. В копланарной линии четный тип волны является основным. Он возбуждается соединением с коаксиальной линией близкой по размерам копланарной линии.

В инженерной практике приходится прибегать к специальным приемам, чтобы удержать фазовый сдвиг между электродами равный 180⁰ по всей длине копланарной линии. Инженерная практика допускает анализ основных характеристик линии в квазистатическом приближении. На рис. 1.14 и рис. 1.15 приведены зависимости 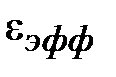, и волнового сопротивления копланарной линии на частоте 30ГГц при d=0,5мм, w=0,05мм.

Рис. 1.14 Рис. 1.15

1.9. Волны напряжения и тока в прямоугольных волноводах

В линиях передачи с ТЕМ волной можно перейти к эквивалентным волнам тока и напряжения (1.23). Общая волновая природа электромагнитных явлений в линиях передачи и волноводах, позволяет перейти к волнам напряжения и тока и в волноводах. В линиях передачи этот переход обоснован введением волнового сопротивления линии, как отношения амплитуды напряжения к амплитуде тока в линии. В свою очередь амплитуды напряжения и тока пропорциональны напряженности электрического и магнитного поля. Поэтому мощность в линиях передачи может быть выражена через напряжение и ток.

В волноводах представляющих собой объем с замкнутыми металлическими стенками, определение разности потенциалов не имеет смысла. Ток на стенках волновода имеет сложный характер, и он не может быть сведен к продольному току в широких стенках волновода. Тем не менее, для прямоугольного волновода в одномодовом режиме с волной H ₁₀ можно ввести “эффективные” напряжения и ток, которые точно отвечают мощности передаваемой по волноводу.

Поверхностный ток на широких стенках волновода продолен в плоскости симметрии волновода при 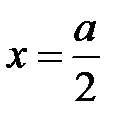и имеет противоположные направления на стенках (1.1), (1.5). Поэтому широкие стенки волновода принято считать проводниками эквивалентной двух проводной линии, по которым течет ток с амплитудой равной интегралу по широкой стенке от продольной компоненты плотности поверхностного тока (1.5)

.

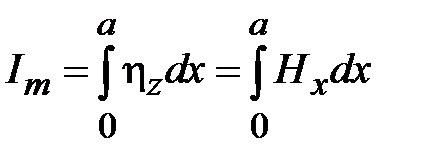Подставим сюда соотношение (1.1), найдем амплитуду продольного тока, текущего по широким стенкам как проводникам двух проводной линии передачи

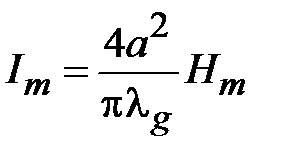. (1.26)

Мощность, передаваемую по волноводу, представим в виде (1.15) как

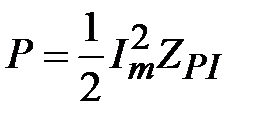, (1.27)

где 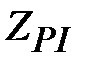- волновое сопротивление, определенное по мощности и току.

Эквивалентный переход от волновода к двух проводной линии передачи состоит в равенстве мощности (1.27) и мощности, определенной через поток вектора Пойнтинга (1.2). Подставим в (1.27) соотношение (1.26), приравняем мощности, передаваемой по волноводу в виде (1.2) и найдем

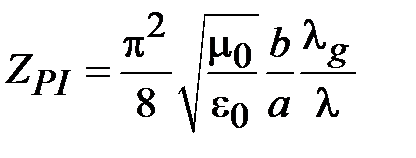. (1.28)

Введем волновое сопротивление волновода, определив эффективное напряжение между широкими стенками как

.

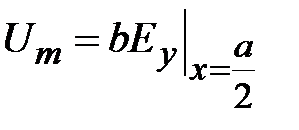Подставим сюда соотношение для 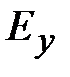из (1.1) получим

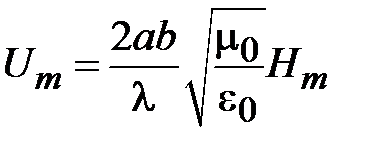. (1.29)

Мощность в линии теперь можно определить через напряжение (1.29) и волновое сопротивление 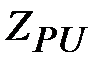как

.

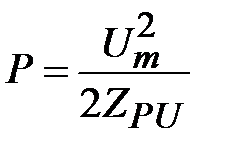Подставим в это соотношение (1.2), (1.29) и найдем, что

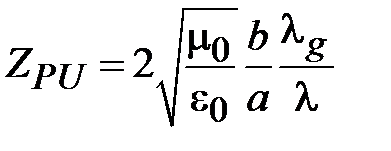. (1.30)

Напряжение и ток, в соотношениях (1.26) и (1.29), позволяют определить волновое сопротивление волновода по напряжению и току

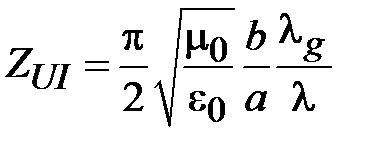. (1.31)

Как видно, формулы для расчета волнового сопротивления прямоугольного волновода с волной H ₁₀ (1.28), (1.30) и (1.31) незначительно отличаются числовыми коэффициентами.

Таким образом, прямоугольный волновод в одномодовом режиме с волной H ₁₀ эквивалентен двух проводной линии передачи, образованной широкими стенками волновода. Ток и напряжение в эквивалентной двух проводной линии, пропорциональны поперечным составляющим электрического и магнитного поля. Поэтому распространение электромагнитной энергии в волноводе можно описать волнами напряжения и тока (1.23), амплитуды которых вычисляются через передаваемую мощность и волновые сопротивления.

2. НЕОДНОРОДНОСТИ В ЛИНИЯХ ПЕРЕДАЧИ. СОГЛАСОВАНИЕ ЛИНИЙ ПЕРЕДАЧИ

2.1. Описание электромагнитного процесса в линиях передачи с неоднородностями

В технике сверх- высоких частот на основе волноводов проектируются устройства различного функционального назначения: фильтры, делители мощности, ответвители и т.д. Любое устройство создается с помощью различных вида перегородок, металлических штырей, диэлектрических шайб и т.п., устанавливаемых в поперечно сечении волновода. На рис. 2.1. показаны некоторые виды металлических перегородок и штыря в прямоугольном волноводе. В электродинамике их принято называть неоднородностями. Неоднородности возникают на стыках линий передачи разных размеров поперечных сечений линий передачи.

Анализ электромагнитного процесса в линиях передачи содержащих неоднородности строится в предположении, что в них распространяется только один основной тип волны: H ₁₀ в прямоугольном волноводе, H ₁₁ в кругом волноводе, ТЕМ в линиях передачи. Поле основной волны в месте расположения неоднородности возбуждает поля высших типов, которые не распространяются по линии передачи, а локализуются вблизи неоднородности. Совокупное электромагнитное поле высших типов волн связано с реактивной энергией, локализующейся вблизи неоднородности. В зависимости от вида неоднородности энергия может накапливаться преимущественно в совокупном магнитном поле, либо в электрическом поле. В зависимости от этого неоднородности можно характеризовать соответствующими эквивалентными параметрами – индуктивными или емкостными. Толщина перегородок, диаметры штырей и т.д. обычно много меньше длины волны в линии передачи, поэтому в ряде случаев их можно считать бесконечно тонкими. Это в свою очередь позволяет считать, что неоднородность не занимает физического объема и, следовательно, ее индуктивную или емкостную реакцию можно соотнести с эквивалентным индуктивным или емкостным сопротивлением (проводимостью) включенным в линию передачи. Представление неоднородностей в виде эквивалентных реактивных сопротивлений неточно, потому, что всякая неоднородность поглощает электромагнитную энергию и, следовательно, имеет активную составляющую эквивалентного сопротивления, но ею можно пренебречь при упрощенном анализе.

Перейдем к описанию электромагнитного процесса в линии передачи с неоднородностью. На рис. 2.2. представлено сечение условной линии передачи в плоскости оси распространения электромагнитной волны. В сечении z=0 расположена неоднородность. Исходным условием анализа является одномодовый режим работы линии передачи. В этом случае, от генератора распространяются падающие волны напряжения и тока

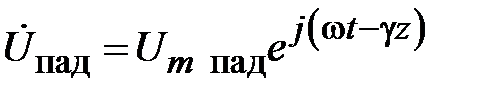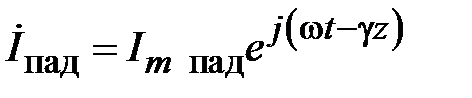, . (2.1)

Мощность падающей волны равна

,

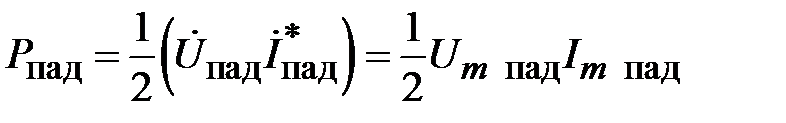где 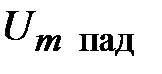, 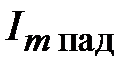- связаны через волновое сопротивление линии

.

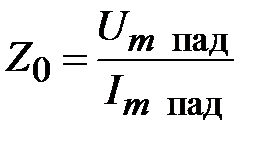При падении волны на неоднородность возникают не только волны высших типов локализующиеся в малом объеме, но и отраженная волна основного типа, распространяющаяся в сторону генератора рис. 2.2. Отраженные волны идентичны падающим и отличаются только значениями амплитуды и фазы. Запишем отраженные волны напряжения и тока в виде

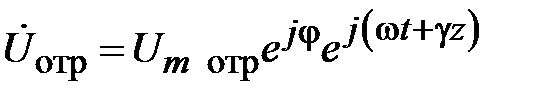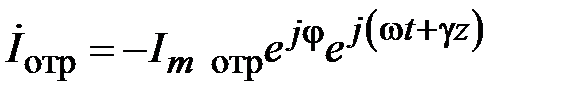, . (2.2)

Отрицательный знак у 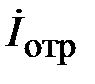, определен распространение волны тока в сторону отрицательного направления оси 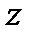. Фазовый сдвиг 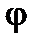в отраженной волне определяется видом неоднородности.

Свойства неоднородности удобно характеризовать коэффициентом отражения. Коэффициент отражения по напряжению в сечении неоднородности определяется как

.

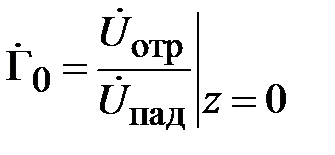Подставим сюда соотношения (2.1) и (2.2), получим

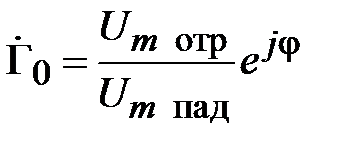. (2.3)

Коэффициент отражения в сечении неоднородности является величиной комплексной: его модуль равен отношению амплитуд напряжения отраженной и падающей волн, а фаза, равна фазе отраженной волны.

Коэффициент отражения по току определяется как

.

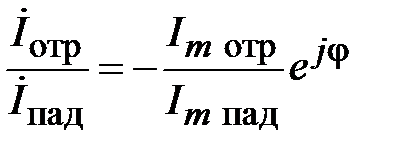Амплитуды тока в падающей и отраженной волне пропорциональны амплитудам напряжения (2.1), поэтому

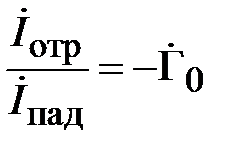. (2.4)

В пространстве между генератором и неоднородностью возникает наложение падающих и отраженных волн. В соответствии с (2.1) и (2.2), найдем их суммы

,

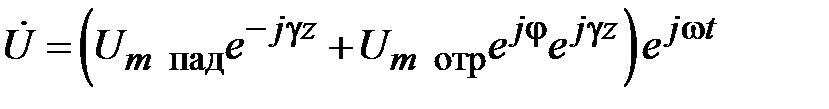(2.5)

.

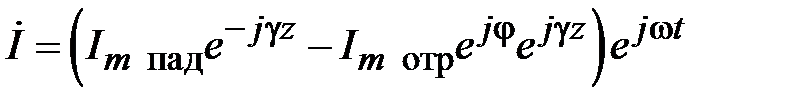Используя соотношения (2.3) и (2.4) преобразуем (2.5) к виду

,

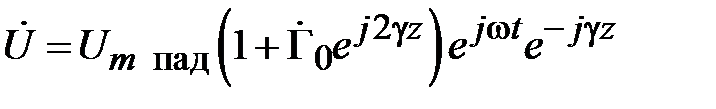(2.6)

.

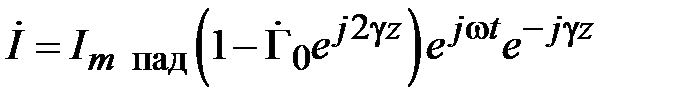Из (2.6) следует, что в результирующих волнах амплитуды напряжения и тока изменяются в зависимости от удаления от неоднородности как

,

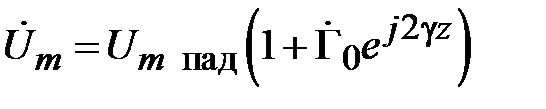(2.7)

.

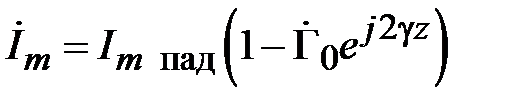Такие волны называют стоячими, а величину

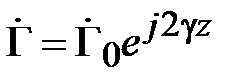, (2.8)

коэффициентом отражения в плоскости z. Его модуль равен модулю 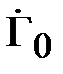, а фаза является непрерывной функцией z.

Найдем явный вид зависимости от 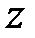амплитуды напряжения стоячей волны. В соответствии с (2.7) и (2.3) запишем

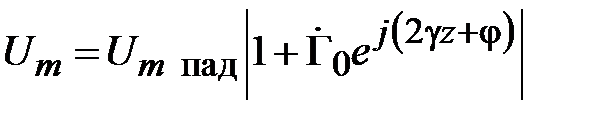. (2.9)

Соотношение (2.9) можно преобразовать к виду

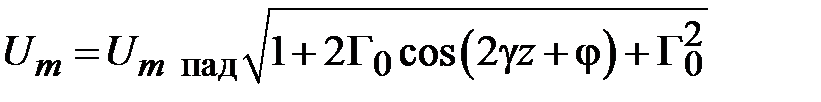. (2.10)

Из (2.10) следует, что амплитуда стоячей волны периодически изменяется между максимальным 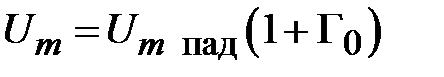и минимальным 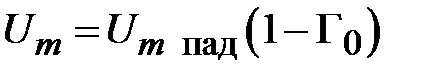значениями с периодом по оси z равным половине длины волны в линии, что определяется аргументом косинуса в (2.10). На рис. 2.3, изображен график зависимости амплитуды стоячей волны от удаления от неоднородности в сторону генератора.

В инженерной практике отношение максимального значения амплитуды стоячей волны к минимальному значению называется коэффициентом стоячей волны по напряжению (КСВН)

.

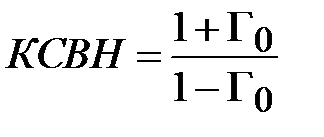Как видно КСВН изменяется в интервале 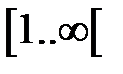в зависимости от значения .

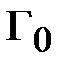Рассмотрим соотношения между мощностями в падающей и отраженной волне. Мощность отраженной волны равна

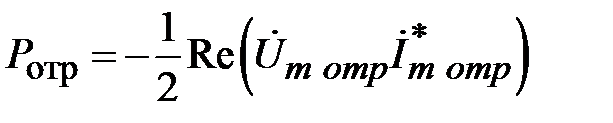. (2.11)

Отрицательный знак в (2.11) определен распространением отраженной волны вдоль отрицательного направления оси 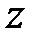. Подставим в (2.11) соотношение (2.2) получим

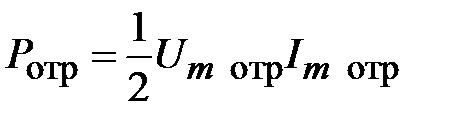. (2.12)

Амплитуды отраженных и падающих волн связаны между собой модулем коэффициента отражения 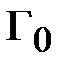(2.3), (2.4). Поэтому 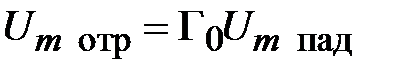, 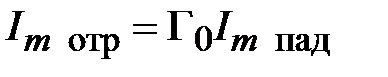. Подставим эти соотношения в (2.12), найдем мощность отраженной волны

.

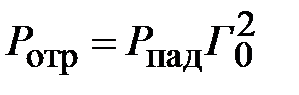В соответствии с балансом мощностей найдем мощность прошедшей волны

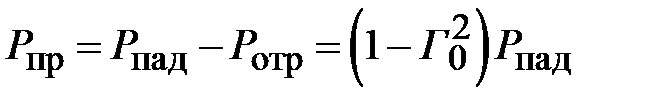, (2.13)

где 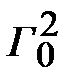- квадрат модуля коэффициента отражения.

2.2. Входное сопротивление отрезка линии передачи

В произвольном сечении оси 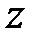между генератором и неоднородностью 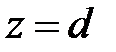отношение напряжения к току в стоячей волне можно считать входным сопротивлением отрезка линии длиной 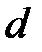. На рис. 2.4 приведено, общепринятое в технической электродинамике схематическое представление произвольной линии передачи с неоднородностью. Неоднородность на рис. 2.4 представлена эквивалентным реактивным сопротивлением 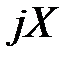. Справа от неоднородности бесконечная линия передачи заменена ее волновым сопротивлением 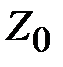. Параллельное соединение сопротивления неоднородности и волнового сопротивления 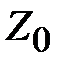образует сопротивление нагрузки 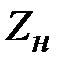. Рис. 2.4 можно видоизменить, вычленив отрезок линии длиной 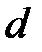, нагруженный на сопротивление 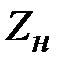рис. 2.5. Найдем входное сопротивление отрезка линии. В соответствии с (2.7) отношение напряжения к току в сечении 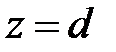равно

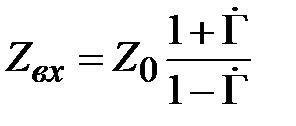, (2.14)

где .

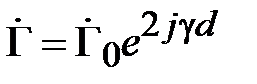Нормируем входное сопротивление в (2.14) к волновому сопротивлению линии, получим

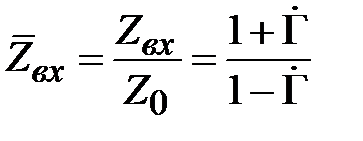, (2.15)

Очевидно, нормированное волновое сопротивление равно единице. Соотношение (2.15) преобразуем к виду

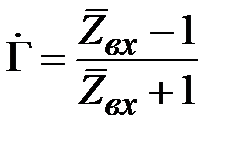. (2.16)

Коэффициент отражения, определяемый соотношением (2.16), вычисляется на входе отрезка линии длинной 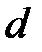, поэтому положив 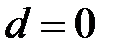можно заменить в (2.16) 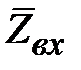на нормированное сопротивление нагрузки 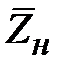. Тогда из (2.16) следует, что коэффициент отражения 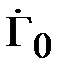в плоскости нагрузки линии передачи равен

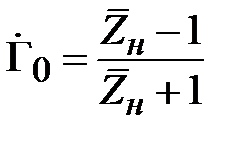. (2.17)

На основании (2.16), (2.14) и (2.17) коэффициент отражения на входе отрезка линии можно преобразовать к виду

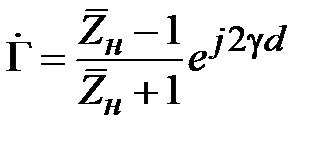. (2.18)

Подставив (2.18) в (2.15), найдем нормированное входное сопротивление отрезка линии передачи в виде

.

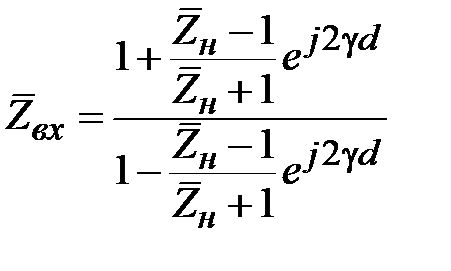Это соотношение после преобразования можно представить в виде

.

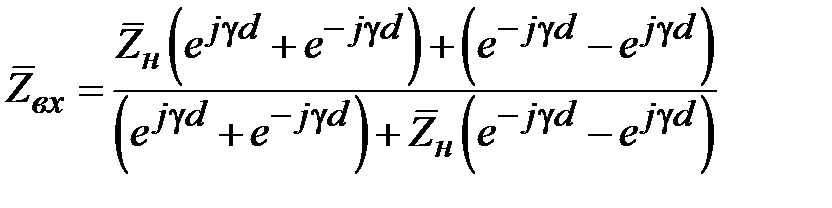Откуда, на основании формул Эйлера следует, что

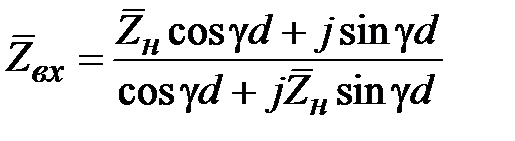. (2.19)

Введем волновую проводимость линии передачи как 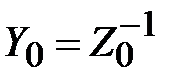, тогда (2.19) можно простым преобразование привести к виду нормированной входной проводимости 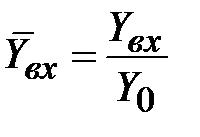отрезка линии передачи в зависимости от нормированной проводимости нагрузки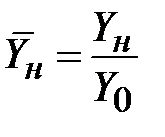

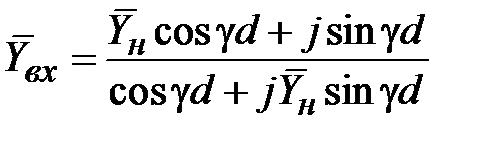. (2.20)

Элементарные преобразования позволяют получить формулы для ненормированных входного сопротивления и входной проводимости в виде

,

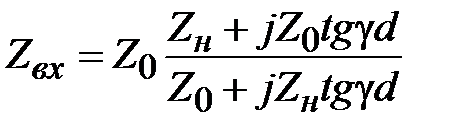(2.21)

.

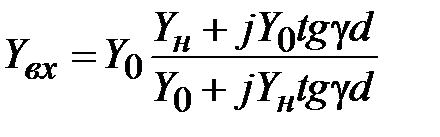Соотношения (2.19), (2.21) получены на основе описания электромагнитного процесса в линиях передачи с помощью падающих и отраженных волн напряжения и тока. Они имеют универсальный характер и могут быть применены к расчету любых линий передачи для которых может быть определено волновое сопротивление и постоянная распространения.

2.3. Трансформирующие свойства отрезка линии передачи

Входное сопротивление отрезка линии (2.19), (2.21) зависит от ее длины и нагрузки. В этом заключается трансформирующее свойство отрезка линии передачи. Рассмотрим важные частные случаи трансформации сопротивлений отрезком линии передачи. Допустим, что в клеммной плоскости нагрузки линия передачи короткозамкнута (к.з.), т.е. 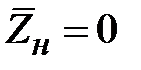. Тогда из (2.21) получим, что нормированное входное сопротивление к.з. отрезка линии передачи равно

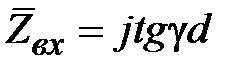. Отсюда следует, что входное сопротивление реактивно и на частотах, для которых выполняется условие 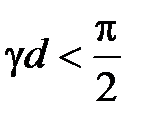, сопротивление имеет индуктивный характер, а при условии 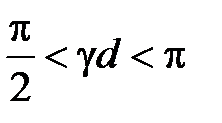, сопротивление имеет емкостной характер. Так как 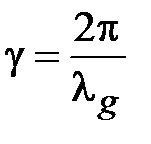, то оба неравенства можно переписать в виде 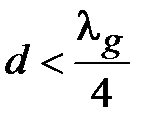, . При 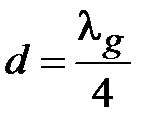входное сопротивление бесконечно велико. Таким образом, к.з. четвертьволновый отрезок линии передачи трансформирует к.з. в холостой ход (х.х.) на входе. Теоретически можно допустить, что четвертьволновый отрезок может быть нагружен на х.х., то есть 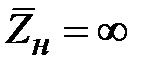. Тогда из (2.16) получим 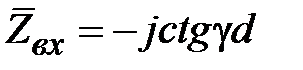. Отсюда следует, что четвертьволновый отрезок линии передачи трансформирует х.х. в короткое замыкание. Полуволновый отрезок 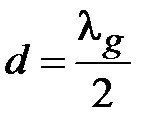( 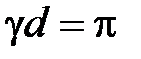) трансформирующими свойствами не обладает: его входное сопротивление в соответствии (2.21) равно сопротивлению нагрузки .

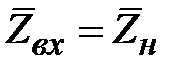Допустим, что нагрузкой отрезка линии передачи является волновое сопротивление 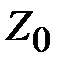. В этом случае при произвольной длине отрезка в соответствии с (2.21) 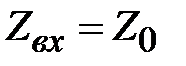и согласно (2.16) коэффициент отражения равен нулю. Такой режим волновода называется согласованным – вся энергия электромагнитного поля попадает в нагрузку без отражения.

Рассмотрим более общий случай трансформации сопротивления отрезком линии передачи. Допустим, что две линии передачи с разными волновыми сопротивлениям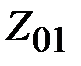и и 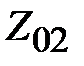соединены последовательно отрезком линии длиной 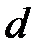с волновым сопротивлением 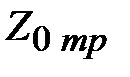. На рис. 2.6.а. представлено это соединение в эквивалентном виде для произвольных линий, а на рис. 2.6.б, возможная практическая реализация для коаксиальных линий. Выясним, при каких условиях возможно согласование двух линий с разными волновыми сопротивлениями отрезком линии включенным между ними. Условием согласование является равенство входного сопротивления сечение 1-1 рис. 2.6.а отрезка линии, нагруженного на 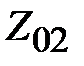, волновому сопротивлению 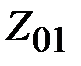. В соответствии с (2.21) запишем условие согласования в виде

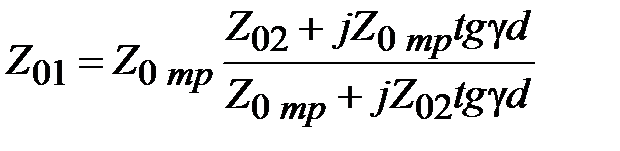. (2.22)

Левая часть равенства (2.22) вещественна, поэтому и правая часть должна быть вещественна. Это возможно только при условии 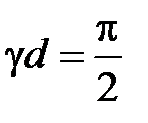( 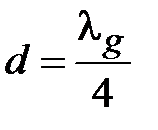). Если это условие выполнено, то из (2.22) следует, что

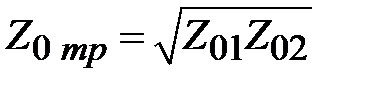. (2.23)

Таким образом, соотношение (2.23) определяет значение волнового сопротивления четверть волнового отрезка линии передачи, который в этом случае выступает, как трансформатор сопротивлений, обеспечивая согласование между линиями передачи с разными волновыми сопротивлениями. Заметим, что полное согласование ( 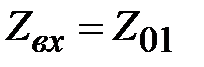) возможно только на одной частоте, соответствующей длине волны в линии при которой 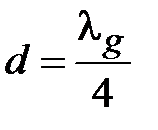. С помощью четверть волнового трансформатора обычно согласуют активные сопротивления, например, как это было показано волновые сопротивления. В общем случае с помощью четверть волнового трансформатора можно согласовать с генератором и комплексную нагрузку. На рис. 2.7 представлена схема согласования нормированной нагрузки 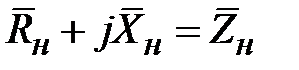с нормированным волновым сопротивлением 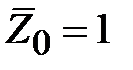. Выбором длины 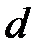отрезка линии передачи рис. 2.7 можно обнулить реактивную часть сопротивления нагрузки, трансформированную в плоскость нагрузки 1-1 четверть волнового трансформатора. В этом случае, трансформатор согласует трансформированное активное сопротивление с единичным нормированным сопротивление линии передачи.

Рассмотрим порядок расчета согласования. В клеммной плоскости нагрузки трансформатора нормированное сопротивление равно

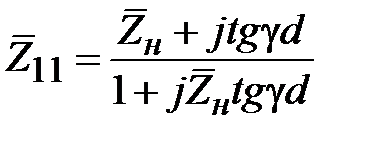. (2.22)

Очевидно, что 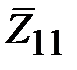комплексная величина. Простым преобразованием (2.22) приведем к виду

,

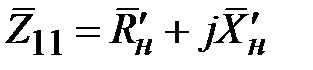где

,

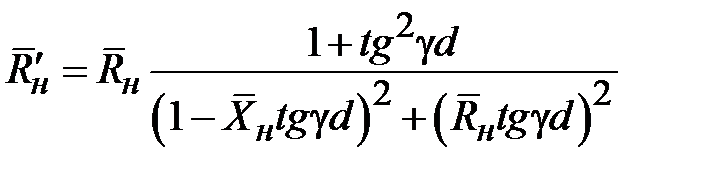(2.23)

.

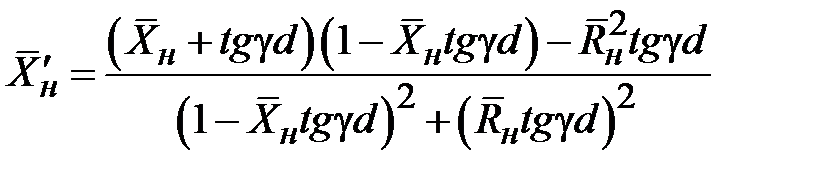Положив 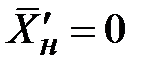, из (2.23) найдем уравнение относительно требуемой длины 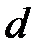отрезка линии передачи

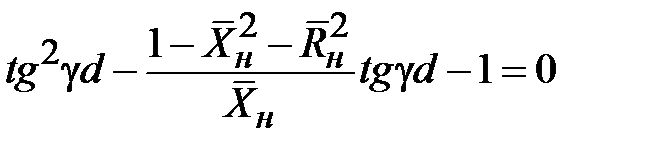. (2.24)

Уравнение (2.24) решается точно относительно 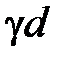. При известном значении 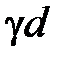по (2.23) вычисляется 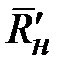. Нормированное волновое сопротивление четверть волнового трансформатора находится как 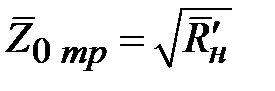. В инженерной практике применяются разнообразные схемы согласования комплексной нагрузки с помощью четверть волнового трансформатора с компенсацией реактивной части сопротивления нагрузки.

2.4. Широкополосное согласование линий передачи

Задачей согласования линий передачи с большим перепадом значений волновых сопротивлений, является обеспечение требуемой частотной зависимости коэффициента отражения. На рис. 2.8 приведена частотная зависимость коэффициента отражения согласуемых линий. Как видно из рисунка, в полосе частот 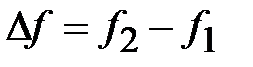коэффициент отражения меньше заданного максимального значения .

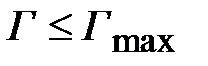Обеспечить требуемую характеристику согласования линии передачи можно каскадным включением четверть волновых трансформаторов между согласуемыми линиями. На рис. 2.9 представлена схема многоступенчатого согласования коаксиальных линий с волновыми сопротивлениям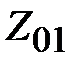и, и 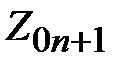. Коаксиальная линия выбрана в качестве примера, а принцип согласования остается неизменным для различных видов согласуемых линий. На рис. 2.9 ( 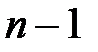) – независимая переменная величина, выбираемая из заданной частотной характеристики согласования, и равная числу четверть волновых трансформаторов. Число стыков (ступенек) и количество четверть волновых трансформаторов одинаково и равно 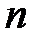. Первая ступенька расположена в клеммной плоскости 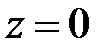. Волновые сопротивления трансформаторов обозначим как 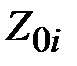, а коэффициенты отражения от стыков 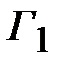.. 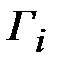, 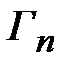. Расчет согласования основан на возможности определения коэффициента отражения в клеммной плоскости первой ступеньки, как суммы коэффициентов отражений от каждой ступеньки с учетом только фазовых набегов, возникающих при прохождении падающих и отраженных волн от каждой ступеньки до клеммной плоскости 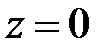. В ином случае, необходимо учесть фазовые сдвиги, вносимые каждым стыком и определять суммарный коэффициент отражения с учетом многократных отражений, возникающих в каскадном включении четверть волновых трансформаторов. Исходное упрощающее допущение сводится к предположению, что коэффициенты отражения от стыков трансформаторов малы. На практике это означает, что волновые сопротивления четверть волновых трансформаторов имеют близкие значения и, следовательно, малые реактивности возникающие на их стыках. Можно установить верхний предел значений коэффициентов отражений, допускающих такое упрощение. Допустим, 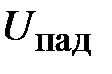- падающая волна напряжения в клеммной плоскости первой ступеньки (рис. 2.9). Мощность, прошедшая через первую ступеньку равна 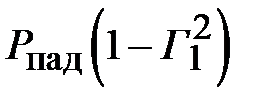, где 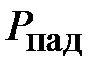- мощность переносимая падающей волной. При условии, что 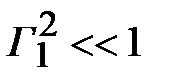мощность, прошедшая после первой ступеньки близка к падающей, это, в свою очередь, означает, что падающая волна напряжения 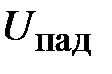с малым ослаблением окажется в клеммной плоскости второй ступеньки. При условии 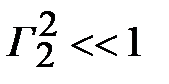можно считать, что падающая волна остается неизменной и равная 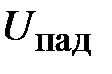. Таким образом, условием равенства падающих волн на каждую ступеньку в волне 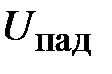, является малое отражение от каждой ступеньки 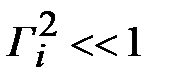. В этом случае отраженные волны от каждой ступеньки складываются в клеммной плоскости первой ступеньки, образуя результирующую отраженную волну. Следовательно, коэффициент отражения в клеммной плоскости 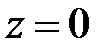можно представить в виде

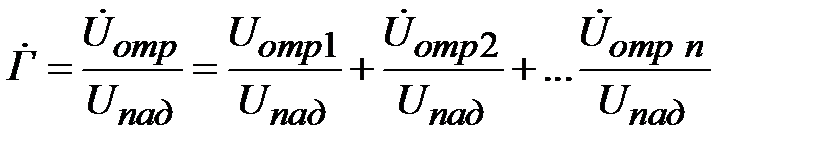. (2.25)

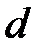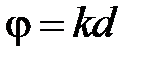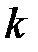Длины четверть волновых трансформаторов одинаковы и равны (рис. 2.9). Обозначим приобретаемый фазовый сдвиг при прохождении волны напряжения на длине одного трансформатора как , где - постоянная распространения одинаковая для всех трансформаторов. Каждое слагаемое в соотношении (2.25) равно коэффициенту отражения от i -той ступеньки 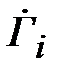с учетом приобретенного фазового сдвига падающей и отраженной волной на длине 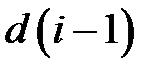. Таким образом

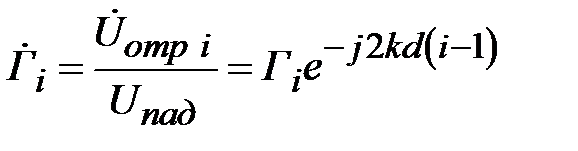, (2.26)

где 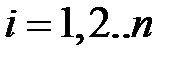- номер ступеньки.

Знак минус в показателе экспоненты означает, что отраженные волны в плоскости 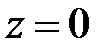складываются с задержкой, равной времени распространения от i –той ступеньки до первой. Таким образом, результирующий коэффициент отражения в плоскости первой ступеньки в соответствии с (2.25) и (2.26) можно представить в виде

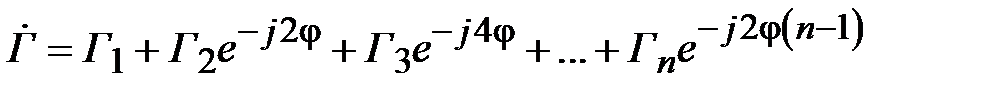. (2.27)

На центральной частоте 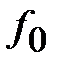полосы пропускания 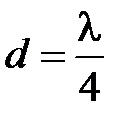, 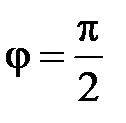и соотношения (2.27) можно преобразовать к алгебраической сумме модулей коэффициентов отражения

.

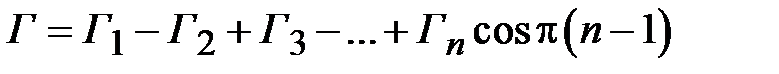Таким образом, существует произвольное число подборов коэффициентов отражений, которые обеспечат 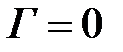на центральной частоте. Простой перебор не позволит получить заданную частотную характеристику. Существуют различные системные способы выбора коэффициентов отражения, обеспечивающие получение требуемой частотной характеристики в заданной полосе частот. Одним из таких правил выбора является биномиальное распределение значений 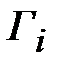, которые пропорциональны коэффициентам бинома Ньютона. Бином Ньютона степени 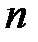содержит 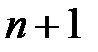членов. В рассматриваемом ступенчатом переходе 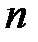- число коэффициентов отражений. Поэтому для согласования числа членов разложения и коэффициентов отражения надо выбрать бином Ньютона степени ( 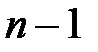). В соответствии с формулой бинома Ньютона имеем

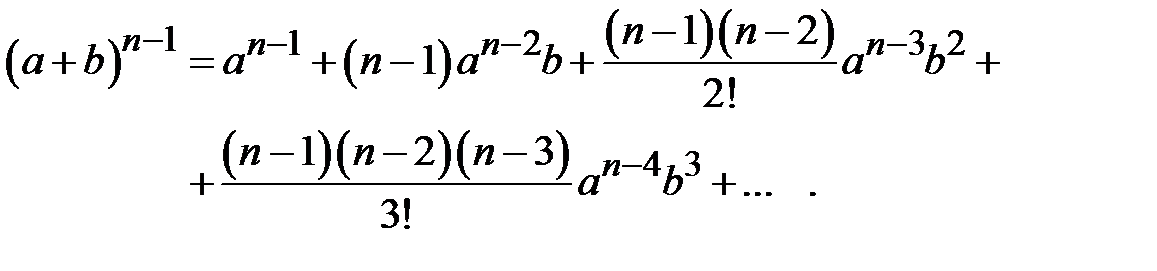
Положим значения модулей коэффициентов отражения пропорциональными коэффициентам разложения бинома. При произвольном значении 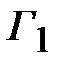получим

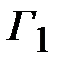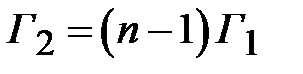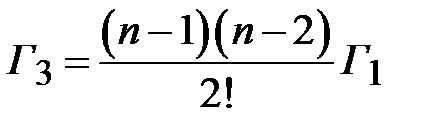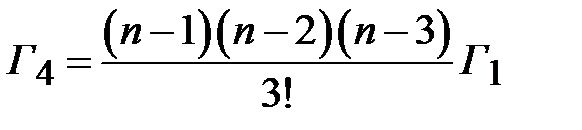, , , , (2.28)

и т.д.

Коэффициенты отражений определяются в соответствии с (2.16) как

,

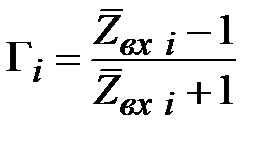где 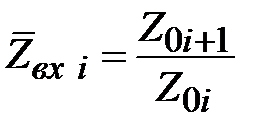, поэтому

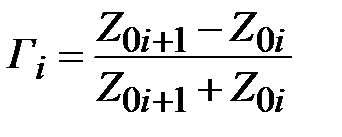. (2.29)

Отношение волновых сопротивлений 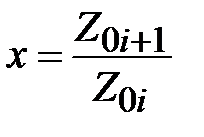близко к единице, поэтому можно считать что 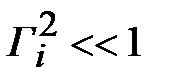. Воспользуемся формулой разложения в степенной ряд функци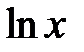и при 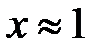и аппроксимируем коэффициенты отражения первым членом ряда 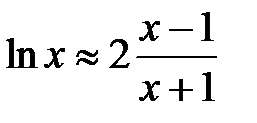. Тогда в соответствии с (2.29) получим

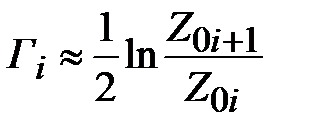. (2.30)

Отклонение точных значений 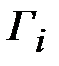(2.28) и приближенного (2.30) не превышает единиц процентов пр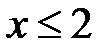и . При 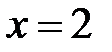, приближенное значение 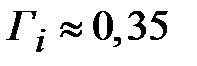, что совпадает с верхней оценкой значения коэффициента отражения, так как можно считать, что 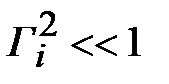. Очевидно, что при 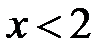, точность расчета возрастает. Например, при 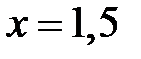, погрешность аппроксимации составляет 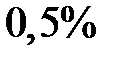, при этом 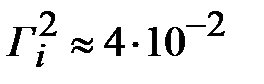. Таким образом, в итерационном расчете, значение отношений волновых сопротивлений на стыке четверть волновых трансформаторов не должно превышать двух.

Найдем сумму модулей коэффициентов отражения от каждой ступеньки. В соответствии с (2.30) найдем

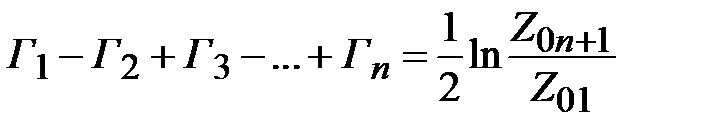. (2.31)

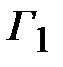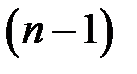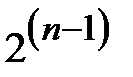В соответствии с биномиальным распределением коэффициентов отражений левая часть (2.31) равна числу кратному . Как известно, сумма коэффициентов разложения бинома Ньютона степени равно . Поэтому соотношение (2.31) можно преобразовать к виду

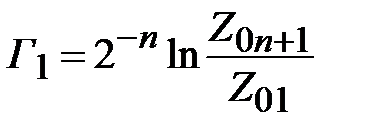. (2.32)

Остальные коэффициенты отражения 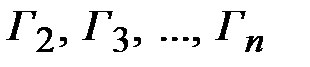вычисляются в соответствии с (2.28). Волновые сопротивления четверть волновых трансформаторов 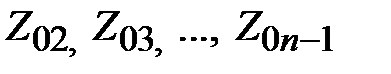определяются из (2.30) как

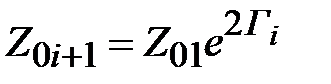. (2.33)

Рассмотрим пример расчета согласования коаксиальных линий с волновыми сопротивлениями 20 Ом и 100Ом.

Выберем трехступенчатый трансформатор. В соответствии с принятыми соотношениями положим 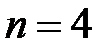. Тогда согласуемые волновые сопротивления 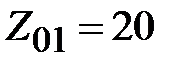Ом, а 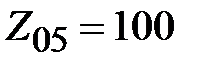Ом. Коэффициент отражения в клеммной плоскости первого четверть волнового трансформатора согласно (2.32) равен

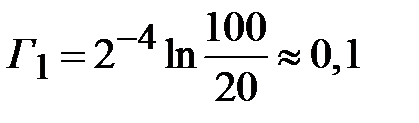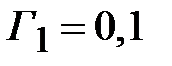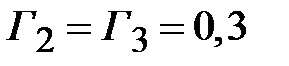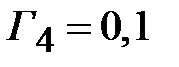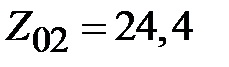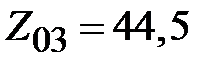. В соответствии с (2.28) коэффициенты отражения на стыках четверть волновых трансформаторов равны , , . Волновые сопротивления трансформаторов вычисляются на основании (2.33) Ом, 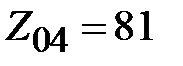Ом, Ом.

Найдем частотную зависимость коэффициента отражения для рассматриваемого примера. В соответствии с (2.27) при 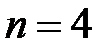результирующий коэффициент отражения равен

.

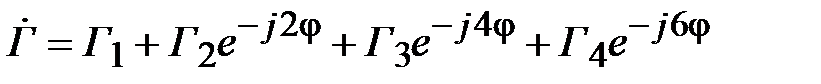Воспользуемся тем, что 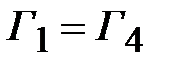, 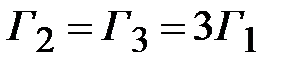и преобразуем это соотношение к виду

.

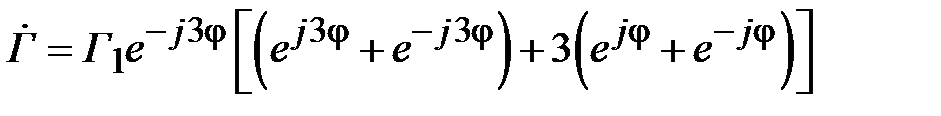В соответствии с формулой Эйлера имеем

.

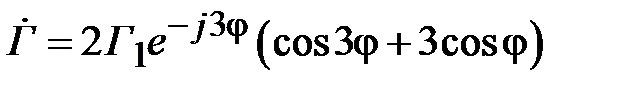Найдем модуль коэффициента отражения

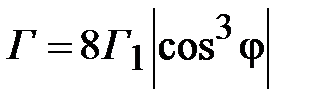. (2.34)

Соотношение (2.34) определяет частотную зависимость коэффициента отражения. Его можно видоизменить, задав допустимое максимальное значение

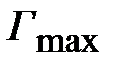. Тогда из (2.34) следует

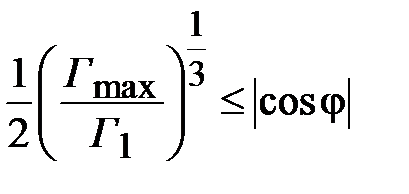. (2.35)

Придадим вносимому фазовому сдвигу явный вид частотной зависимости 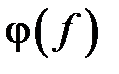. Положим 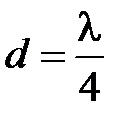на частоте 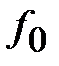. Обозначим 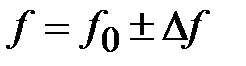. Тогда 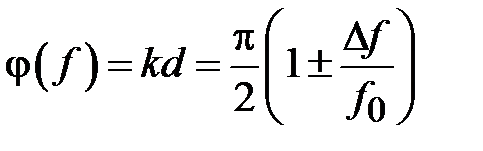. Из (2.35) найдем максимальное значение 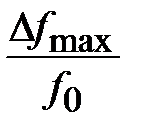удовлетворяющее соотношению

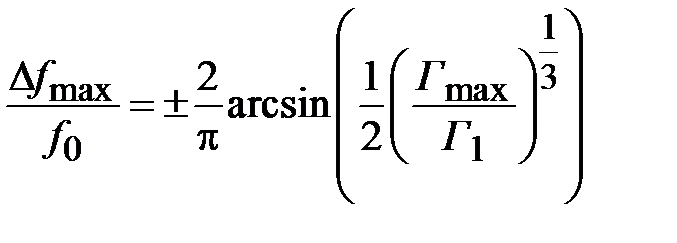. (2.36)

Допустим, что в рассматриваемом примере максимальное значение коэффициента отражения задано равным 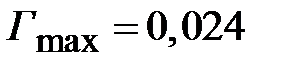(при этом максимальное значение 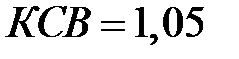). Из (2.36) найдем, что 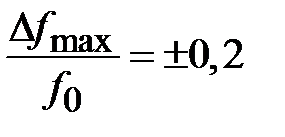, что отвечает ширине полосы пропускания 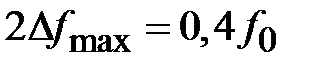. На рис. 2.10 приведена расчетная частотная зависимость коэффициента отражения. Биномиальные четверть волновые согласующие переходы обладают максимально плоской частотной характеристикой коэффициента отражения.

2.5. Круговая диаграмма сопротивлений

Круговая диаграмма сопротивлений является графическим представлением коэффициента отражения, определяемого формулой (2.16). Покажем способ построения круговой диаграммы. Коэффициент отражения 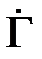, как и сопротивление в выбранной клеммной плоскости 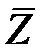, являются комплексными величинами. Поэтому представим

,

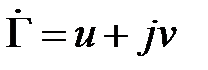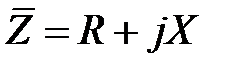, (2.37)

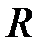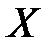где и - нормированные величины.

Вещественную и мнимую части коэффициента отражения ( 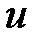, 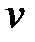) можно рассматривать как координаты, в которых определяется коэффициент отражения. В свою очередь коэффициент отражения связан с 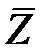через соотношение (2.16) и, следовательно, значения 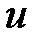и 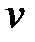зависят от 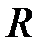и 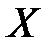. Найдем эту связь в явном виде. Подставим (2.37) в (2.16) получим

.

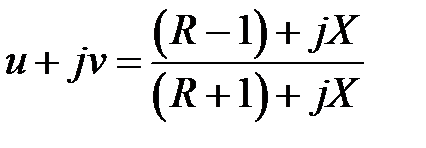Приравняем действительные и мнимые части этого соотношения, получим

,

.

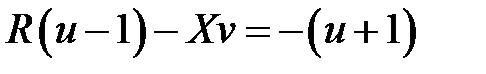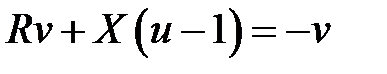Из этой пары уравнений найдем искомые зависимости

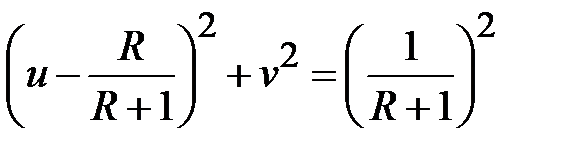, (2.38)

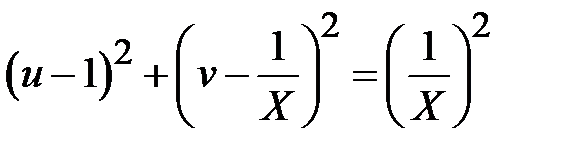. (2.39)

Соотношения (2.38) и (2.39) представляют собой уравнения окружностей в системе координат 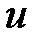и 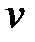. Уравнение (2.38) описывает окружности с центрами расположенными на оси 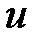в точках 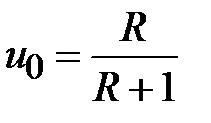, с радиусом 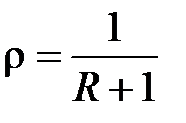. Все окружности проходят через точку 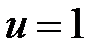, 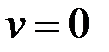. На этих окружностях постоянно значение нормированного сопротивления вещественной части сопротивления в клеммной плоскости. На рис. 2.11 представлены окружности для разных значений 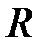. Центр окружности, отвечающей нулю вещественной части 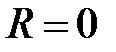, лежит в начале координат 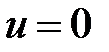, , 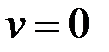а радиус равен единице. Центр окружности соответствующей 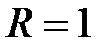лежит в точке 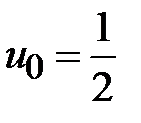, 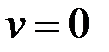и радиус равен 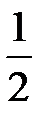. При увеличении 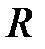уменьшается радиус окружностей, а положение их центров стремятся к точке 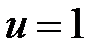, 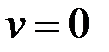. Точка 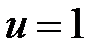, 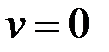отвечает бесконечно большому значению 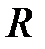и, следовательно, режиму холостого хода.

Перейдем к уравнению (2.39), описывающему окружности радиуса 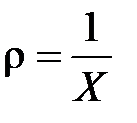постоянного значения реактивного сопротивления 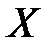, центры которых лежат на прямой 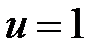, 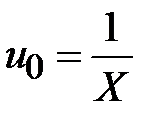. Все окружности проходят через точку 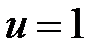, 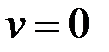. С уменьшением 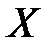радиусы окружностей увеличиваются, а центры стремятся к точке 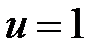, 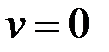. В пределе холостого хода окружности вырождаются в координатную линию 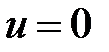. На рис. 2.12 построено семейство окружностей, отвечающих индуктивным и емкостных значениям 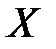, модули которых одинаковы. На рис. 2.13 представлены совмещенные кривые равных 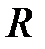и 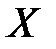. Для расширения возможностей круговой диаграммы на нее наносят линии постоянных значений коэффициентов стоячей волны, которые являются концентрическими окружностями с центрами в начале координат 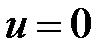, 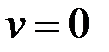. Полному согласованию отвечает центр окружностей в котором 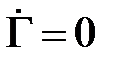, что в соответствии с определением 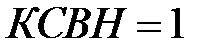. Полному рассогласованию отвечает окружность радиуса 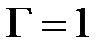, т.е. окружность постоянного значения .

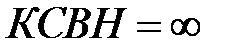Круговую диаграмму можно интерпретировать в терминах входной проводимости, имея в виду, что

,

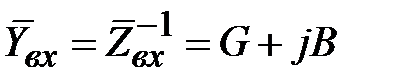где , .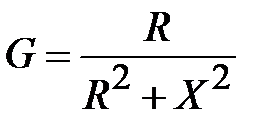

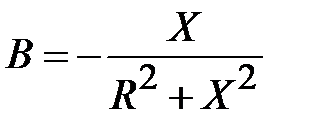Основанием для перехода к круговой диаграмме проводимостей служит соотношение (2.18), которое аналогично соотношению (2.12) и (2.13). В диаграмме проводимостей сохраняются числовые обозначения диаграмма сопротивлений, но с изменением физического смысла характерных точек. На диаграмме проводимостей точка с координатами 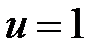, 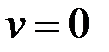означает режим короткого замыкания, а точка равная 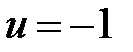, 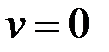соответствует холостому ходу. Верхняя полуплоскость диаграммы ( 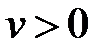) соответствует, по-прежнему, положительной реактивности, но емкостного характера. Нижняя полуплоскость сохраняет отрицательную реактивность, но соответствует индуктивной проводимости. Круговые диаграммы сопротивление или проводимостей отвечают реальной неоднородности, включенной параллельно или последовательно в линию передачи. Для волноводов любая неоднородность в плоскости 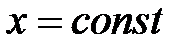на поперечном сечении эквивалентна ее параллельному включению, т.е. шунтирующей проводимости. Неоднородности в виде разрыва или изменения диаметра центрального проводника коаксиальной линии эквивалентна последовательному включению реактивного сопротивления в линию. С помощью круговой диаграммы можно получить решение уравнений (2.12), (2.16) и (2.18).

3. ВОЛНОВОДНЫЕ СИММЕТРИЧНЫЕ УСТРОЙСТВА

3.1. Нормированные волны напряжения и тока. Матрица рассеяния

Описание электромагнитного процесса в линиях передачи с помощью волн напряжения и тока может быть распространено на описание электромагнитного процесса в сочленениях нескольких линий (или волноводов), образующих устройства различного функционального назначения. В этом случае волноводы (линии) передачи представляются эквивалентными двухпроводными линиями с определенными значениями волновых сопротивлений и постоянных распространения. Поэтому произвольное сочленение одинаковых волноводов (передающих линий) может быть представлено в виде волнового многополюсника с произвольным числом входов, рис. 3.1. В клеммных плоскостях каждого входа многополюсника заданы падающие и отраженные волны напряжений и токов. 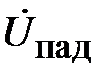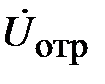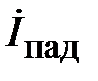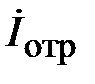В каждой клеммной плоскости входа заданы , и , , которые определены соотношениями (2.1), (2.2). Выполним нормировку токов и напряжений многополюсника. Будем считать, что многополюсник образован одинаковыми волноводами (линиями передачи) с нормированным волновым сопротивлением 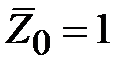. Тогда, мощности падающих и отраженных волн на каждом входе равны

, .

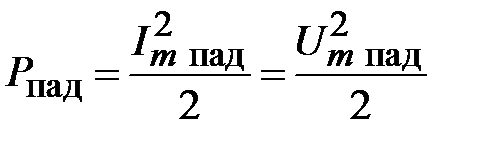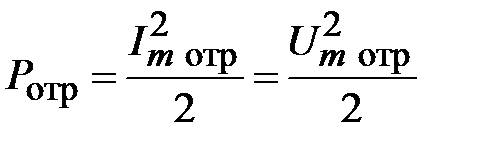Отсюда следует, что амплитуды напряжений и токов в линиях с нормированным волновым сопротивлением одинаковы и равны

, .

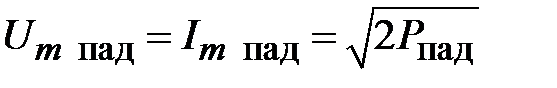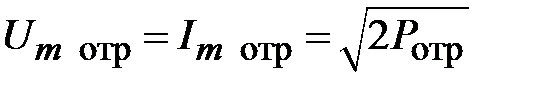Поэтому, падающим и отраженным волнам напряжения и тока, можно соотнести нормированные волны, заменив

, ,

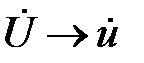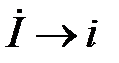где , , .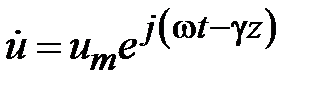

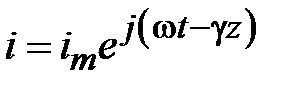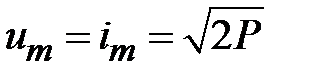Очевидно, что мощность нормированной волны равна мощности переносимой электромагнитной волной. Действительно при выбранной нормировке мощность нормированной волны равна

.

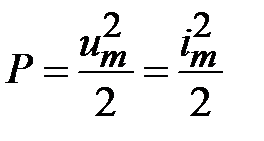На каждом входе многополюсника в общем случае, возникают стоячие волны напряжения и тока как результат сложения падающих и отраженных волн. Запишем стоячие нормированные волны напряжения и тока в виде

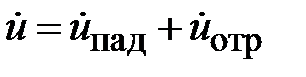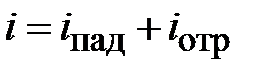, , (3.1)

где 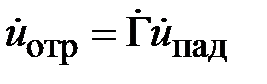, , 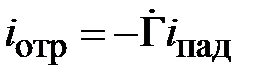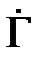- коэффициент отражения в клеммной плоскости входной линии многополюсника.

Падающие и отраженные нормированные волны связаны между собой через волновые сопротивления линий. Поэтому, для нормированных волн имеем

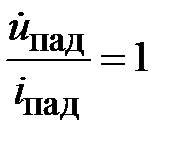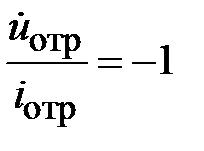, . (3.2)

Таким образом, стоячие нормированные волны (3.1) в соответствии с (3.2) могут быть представлены в виде

,

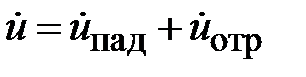(3.3)

.

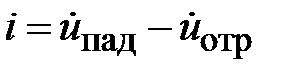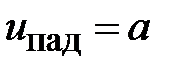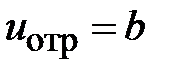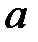Как видно, нормировка волнового сопротивления приводит к “универсальному” представлению волн тока и напряжения (3.3). Поэтому, положим , , где и 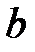комплексные величины, и представим стоячие нормированные волны (3.3) как

,

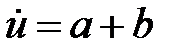(3.4)

.

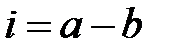На основании соотношений для мощности очевидно, что

, .

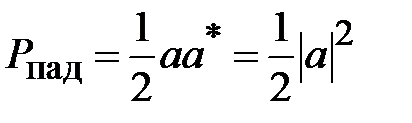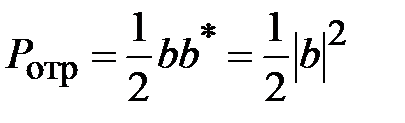Из (3.4) следуют обратные соотношения

,

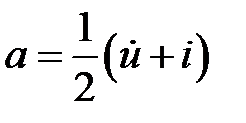(3.5)

.

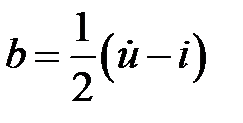Из (3.5) видно, что падающие и отраженные волны являются линейными комбинациями нормированных стоячих волн напряжения и тока. Коэффициент отражения в произвольной плоскости волноводов, образующих многополюсник, для нормированных волн в соответствии с (2.16) и (3.5) определяется как

,

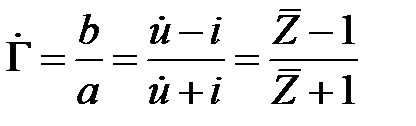где 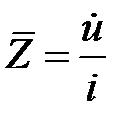- нормированное сопротивление в произвольной плоскости волновода.

Таким образом, между волнами напряжения и тока в линиях передачи (волноводах) и нормированными волнами существует полное соответствие.

Вернемся к эквивалентной схеме многополюсника рис. 3.1. Амплитуды падающих нормированных волн на его входах определяются уровнем мощности, поступающим на соответствующий вход, и не зависят от выбора клеммной плоскости. Однако, положение клеммной плоскости на входе многополюсника в системе координат реального сочленения определяет фазовый сдвиг в падающей волне. У симметричных сочленений физическая длина плеч (входных волноводов или линий передачи) одинакова, поэтому фазовый набег от входных клеммных плоскостей до многополюсника одинаков для всех плеч, и его можно положить равным нулю. Многополюсник считается согласованным по произвольному входу (плечу) если отраженная волна в нем равна нулю. У многополюсника согласованного по j- тому плечу 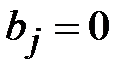. В теории волновых многополюсников, отраженные волны на входных клеммных плоскостях называются рассеянными волнами. Таким образом, нормированные волны 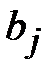во всех плечах являются рассеянными волнами. Падающие и рассеянные волны, создают универсальный образ волнового многополюсника. При подключении источника поля к произвольному j – тому входу в нем может появиться рассеянная (отраженная) волна 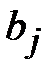, если плечо не согласовано с многополюсником, но в других плечах появятся рассеянные волны, даже если они подключены к согласованным нагрузкам. Амплитуды рассеянных волн пропорциональны амплитудам падающих волн 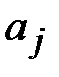на j – том входе. При подключении источников поля к нескольким плечам (входам), рассеянные волны будут линейными комбинациями падающих волн на соответствующих входах. Между падающими и рассеянными волнами в многополюсники существует линейная связь, которая описывается системой линейных алгебраических уравнений вида

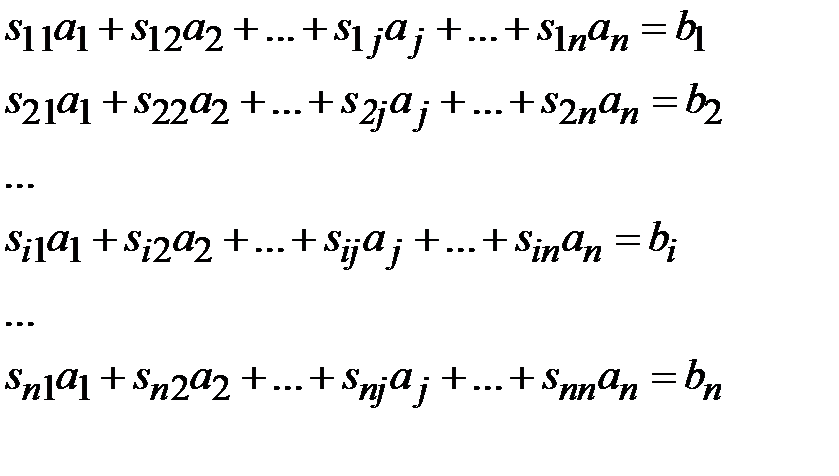. (3.6)

Обозначим векторы падающих и рассеянных нормированных волн как векторы столбцы

, .

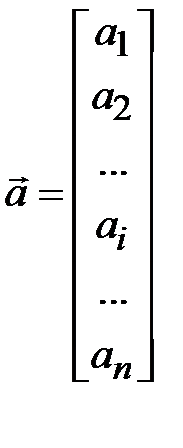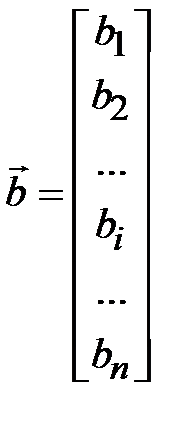На основании правил матричной алгебры представим (3.6) в виде

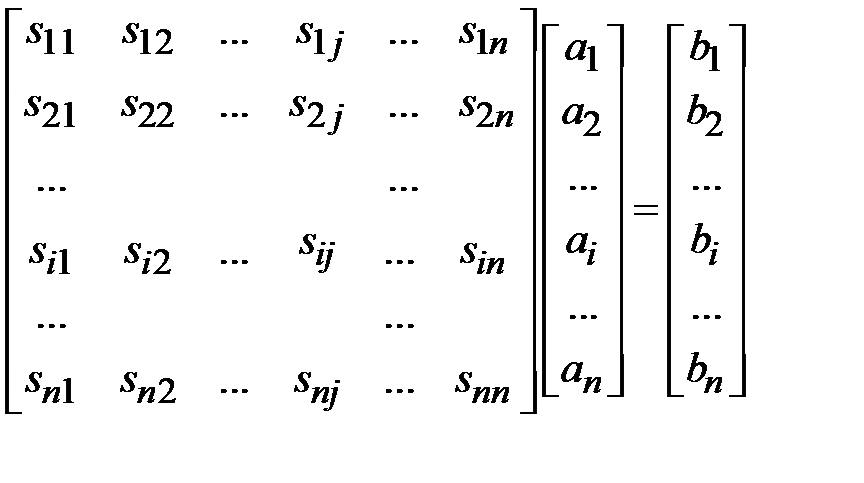. (3.7)

Матрица системы линейных уравнений (3.6), (3.7)

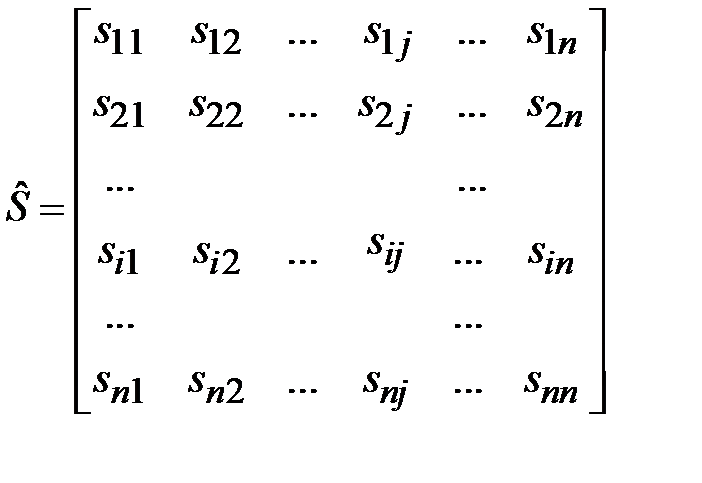, (3.8)

называется матрицей рассеяния волнового многополюсника.

3.2. Свойства матрицы рассеяния

Каждое уравнение в системе линейных уравнений (3.6) может быть представлено в виде

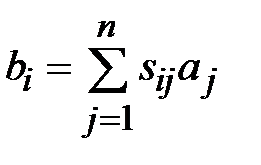. (3.9)

Соотношение (3.9) показывает, что рассеянная волна в i – том плече многополюсника является линейной комбинацией падающих волн. Поэтому физический смысл элементов матрицы рассеяния легко выявляется из (3.9). Допустим, что источник электромагнитного поля подключен к j – тому плечу, а все остальные плечи многополюсника согласованы с нагрузками. Это означает, что 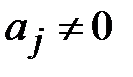, а во всех остальных плечах 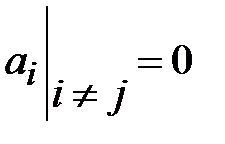. Тогда из соотношения (3.9) следует, что

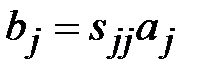. (3.10)

Отсюда очевидно, что

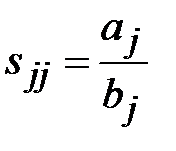. (3.11)

В соответствии с определением коэффициента отражения из (3.11) следует, что 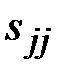- коэффициент отражения по входу j –того плеча, при условии, что остальные плечи согласованы. Очевидно, что 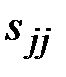в общем случае величина комплексная, так как между падающей и рассеянной волной возможен фазовый сдвиг. Таким образом, на главной диагонали матрицы рассеяния стоят коэффициенты отражения по соответствующим плечам. Недиагональный элементы определяют рассеянные волны в i – том плече при условии, что источник поля включен в j – тое плечо и все плечи согласованы. При этом условии из (3.9) следует, что

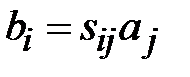. (3.12)

Мощность рассеянной волны в i –том плече равна 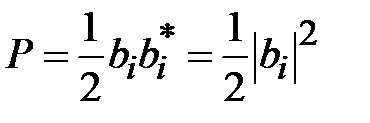. В общем случае 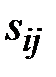комплексные величины. Поэтому, мощность рассеянной волны в соответствии с (3.12) равна 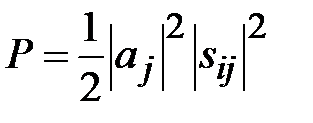. Квадрат модуля нормированной падающей волны равен мощности в j – том плече. Таким образом 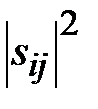определяет долю мощности, поступающей из j – того плеча в i – тое плечо. Поэтому 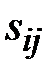можно считать коэффициентами связи (передачи) между соответствующими плечами.

Практический интерес представляют волноводные сочленения, обладающие пространственной симметрией. Сочленение симметрично, если оно переходит само в себя при отражении от плоскости или при повороте вокруг оси. Для симметричных сочленений 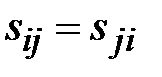и матрица рассеяния (3.8) симметричного 2n - полюсника принимает вид

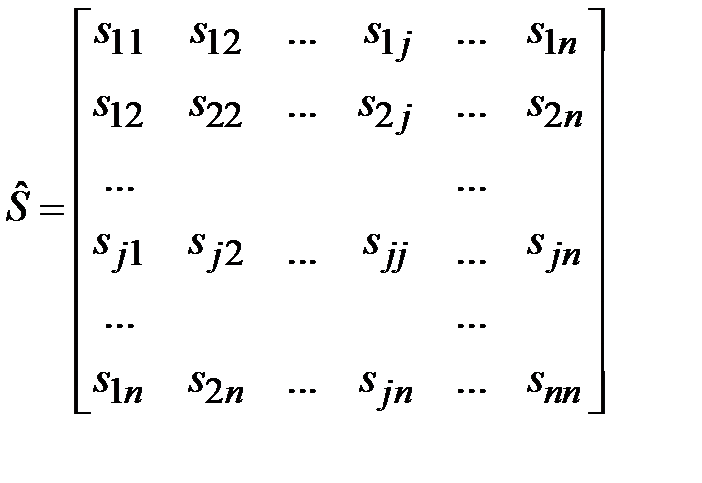. (3.13)

Баланс мощностей в волноводном многополюснике при отсутствии в нем потерь, следуют из унитарности матрицы рассеяния. Матрица унитарна если

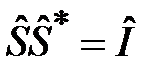, (3.14)

где 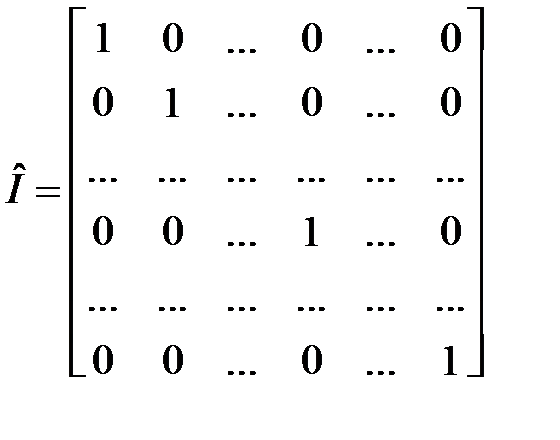- единичная матрица.

Из (3.14) по правилу матричной алгебры следует, что

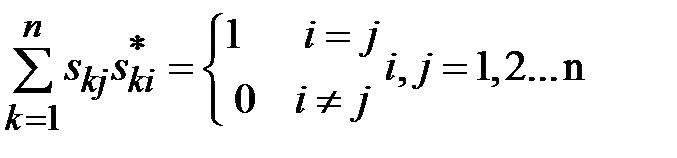, (3.15)

где i – номер строки, j – номер столбца.

Для симметричных сочленений соотношение (3.15) может быть представлено в виде:

суммы квадратов модулей элементов матрицы рассеяния по строкам (столбцам) равны единице

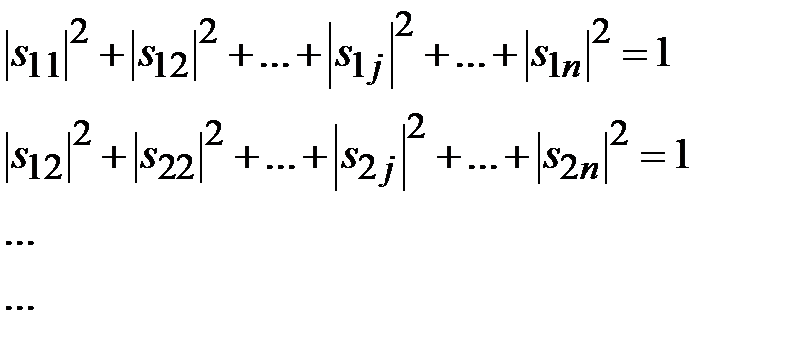; (3.16)

суммы почленных произведений строк (столбцов) элементов матриц 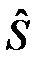и 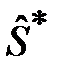равны нулю

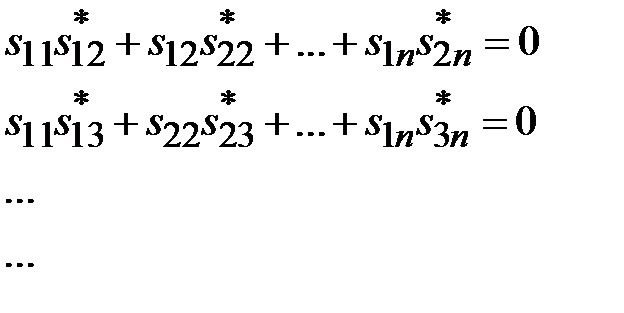. (3.17)

Соотношение (3.16) представляют собой уравнения баланса мощности в многополюснике. При условии, что единичная мощность поступает на вход одного из плеч многополюсника, мощность, прошедшая в многополюсник делится между его плечами в соответствии с уравнениями (3.16). Например, при подключении источника поля к входу первого плеча, мощность, прошедшая в многополюсник равна 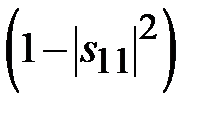и из (3.16) следует, что

,

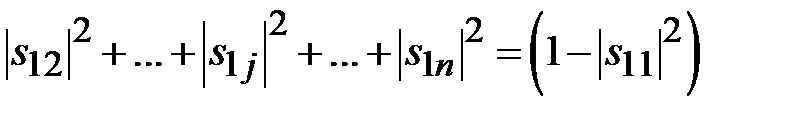где слагаемые левой части пропорциональны мощностям во всех остальных плечах многополюсника.

В заключении рассмотрим волновой четырехполюсник как простейшее многополюсное соединение. На рис. 3.2 изображен четырехполюсник с двумя клеммными плоскостями 1, 2, одну из которых считают входной, а другую выходной. Падающие и рассеянные волны в этих плоскостях обозначены 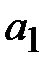, 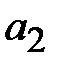и 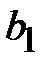, 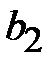. Линейная связь между ними, устанавливается парой алгебраических уравнений, которые в соответствии с (3.6) записываются в виде

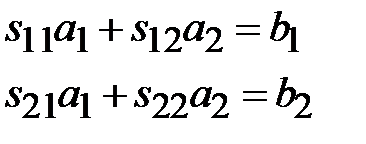. (3.18)

У симметричных четырехполюсников недиагональные элементы равны 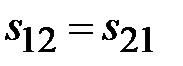. В отсутствии потерь матрица рассеяния четырехполюсника унитарна и в соответствии с (3.16), (3.17) элементы симметричной матрицы рассеяния удовлетворяют уравнениям

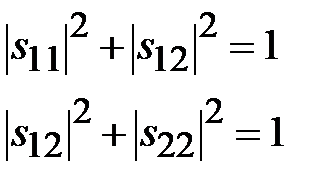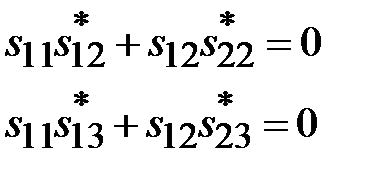, . (3.19)

Из (3.19) следует, что квадраты модулей коэффициентов отражений в клеммных плоскостях .

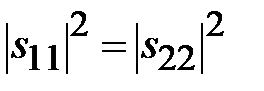Четырехполюсники могут соединяться каскадно. Для двух каскадно соединенных четырехполюсников рис. 3.3 входная волна второго четырехполюсника является выходной волной первого четырехполюсника. Изменив направления падающих и рассеянных волн второго четырехполюсника на противоположные, можно представить линейную связь между входными и выходными волнами в виде

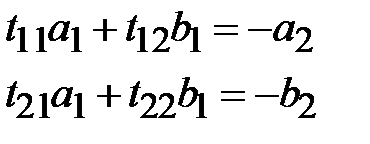. (3.20)

Матрица системы уравнений (3.20) называется матрицей передачи четырехполюсника

.

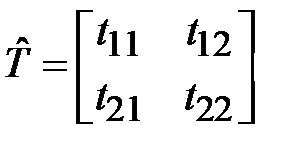Из (3.18) и (3.20) можно установить связь между элементами матриц рассеяния и передачи. Опуская подробности, запишем эти соотношения для симметричного четырехполюсника в окончательном виде

.

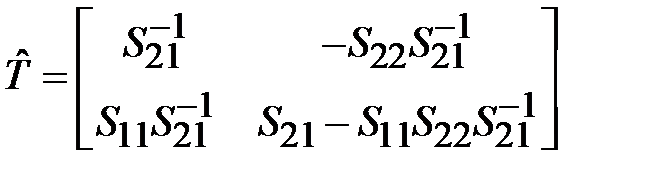Для каскадного соединения четырехполюсников, результирующая матрица передачи равна произведению матриц передачи отдельных четырехполюсников. Это имеет большое практическое значение при анализе цепей образованных каскадным включением четырехполюсников.

3.3. Матрица рассеяния Т – образного тройника в Е плоскости

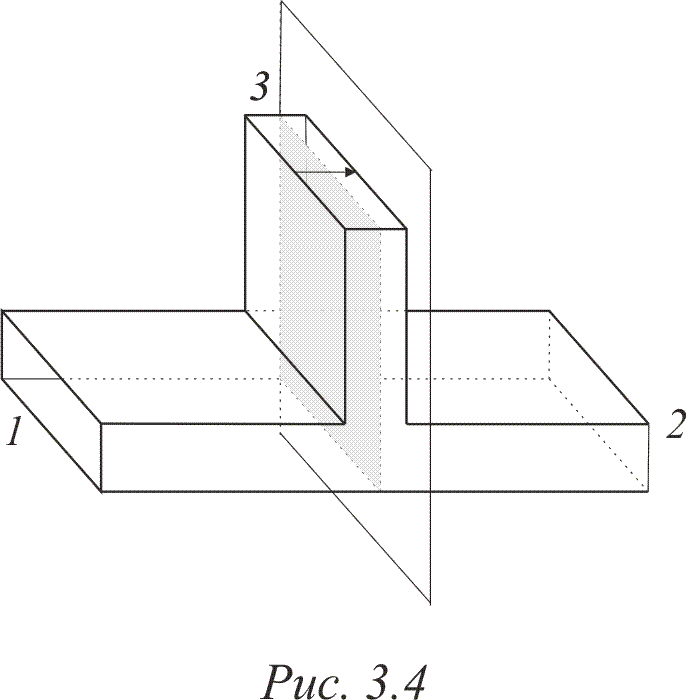Выполним расчет матрицы рассеяния симметричного Т – образного тройника, образованного соединением прямоугольных волноводов, показанным на рис. 3.4. Тройник симметричен относительно одной плоскости симметрии: горизонтальные плечи совмещаются друг с другом при отражении в плоскости симметрии.

Преобразованию симметрии (отражению в плоскости) можно соотнести оператор 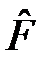, который преобразует вектор падающих 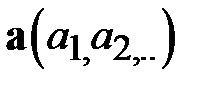и рассеянных 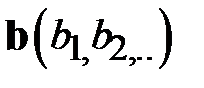волн в исходной конфигурации в новые векторы 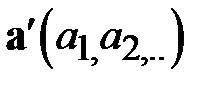, , 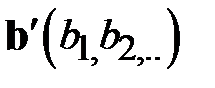отвечающие новой конфигурации, которая отличается только переменой нумерации плеч сочленения 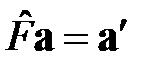, 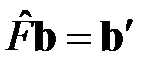. Оператор 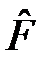, отвечающий за перемену нумерации входов, представляет собой матрицу, в каждой строке и столбце которой стоят 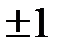, а остальные элементы равны нулю. Отрицательный знак означает возможное изменение поляризации волны на противоположную при отражении. Новые векторы падающих и отраженных волн связаны между собой матрицей рассеяния, которая инвариантна преобразованиям симметрии, поэтому 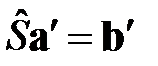. Из этого соотношения следует, что 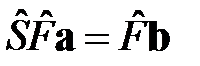. В исходной конфигурации 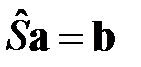, поэтому получим 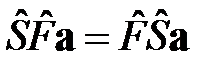. Таким образом, матрицы 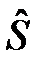и 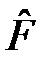коммутативны, то есть 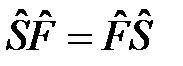. Умножим соотношение коммутативности справа на обратную матрицу 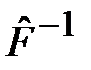, получим 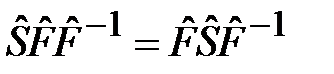или 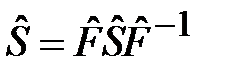. Можно показать, что обратная матрица 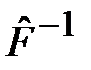, образованная нулями и единицами элементами равна своей транспонированной 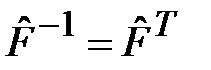. Для симметричной матрицы 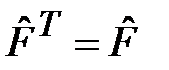. Таким образом, матрица 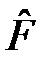, отвечающая операции симметрии определяет свойства матрицы рассеяния через соотношения 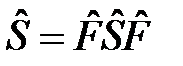или .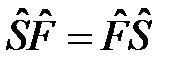

Запишем оператор 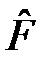, отвечающий операции отражения в плоскости симметрии E – тройника рис. 3.4. Из общих соображений ясно, что при отражении плечи тройника один и два меняются местами, а при отражении третьего плеча происходит изменение знака электрического поля на противоположное. Поэтому матрицу 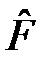можно представить в виде 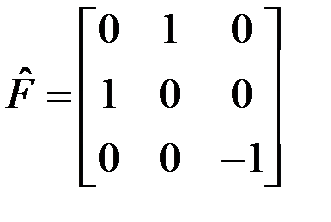. Матрица рассеяния тройника симметричная, поэтому соотношение коммутативности 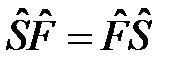принимает вид

.

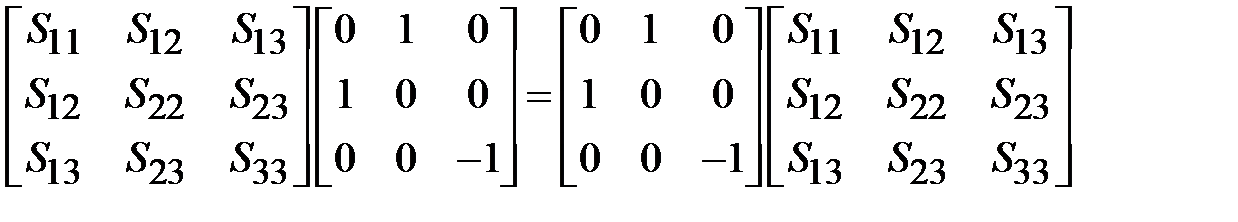После перемножения матриц получим

.

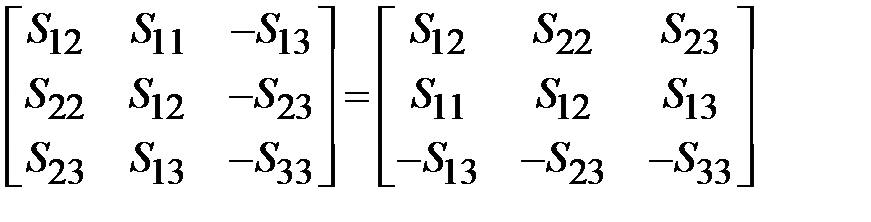Матрицы равны, если равны элементы, стоящие на одинаковых позициях, следовательно, 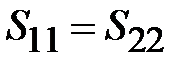и 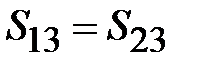. Поэтому матрица рассеяния Е тройника, отвечающая его симметрии должна иметь вид

.

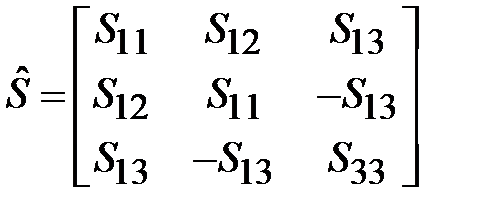Если тройник не имеет потерь, то матрица 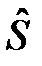унитарная. Из свойств унитарности (3.16), (3.17) следует, что

, .

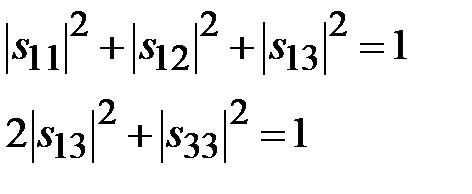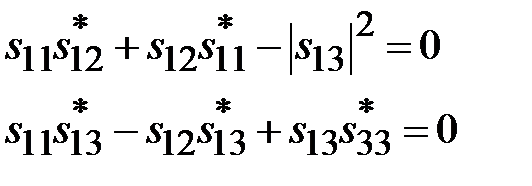Элементы матрицы вещественны, поэтому 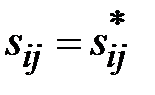, а квадраты модулей 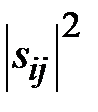равны значениям квадратов элементов матрицы рассеяния. Как видно, преобразование симметрии допускает, что в общем случае 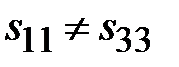, 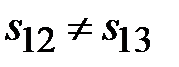. Это отвечает конструкции Е тройника рис. 3.4, в которой узкие стенки вертикального и горизонтального волноводов не равны друг другу. При этом соединение волноводов сохраняет симметрию относительно плоскости отражения.

Перейдем к вычислению элементов матрицы рассеяния на основании эквивалентного представления волноводного Е тройника. В эквивалентном представлении волноводы заменяются двухпроводными линиями, физическим аналогом которых являются широкие стенки волноводов. Поэтому, в рассматриваемом соединении линии передачи, эквивалентные волноводам, соединены последовательно и образуют волновой шестиполюсник рис. 3.5а. Рассмотрим матрицу рассеяния тройника образованного идентичными волноводами. В этом случае для нормированных волн волновые сопротивления эквивалентных линий передачи одинаковы и равны единице. Элементы матрицы рассеяния определяются при условии согласования плеч. Поэтому, сопротивления нагрузки в плоскости симметрии у всех трех плеч шестиполюсника одинаковы и равны удвоенному нормированному волновому сопротивлению. На рис. 3.5.б. представлена эквивалентная схема плеч тройника каждая из которых нагружена на последовательное соединение волновых сопротивлений других двух плеч. Следовательно, диагональные элементы матрицы рассеяния тройника равные коэффициентам отражения одинаковы. В соответствии с определением коэффициента отражения в линии с волновым сопротивлением 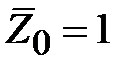нагруженной на 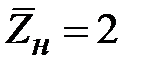(без учета реактивности в месте соединения волноводов) (2.17) получим, что .

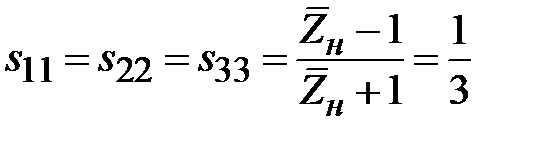Из свойств унитарности матрицы рассеяния следует, что 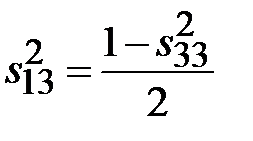, и 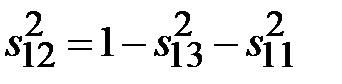. Таким образом 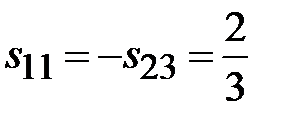, 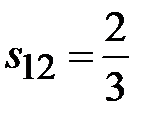. Выбор отрицательного знака у 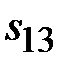или 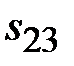произволен. Противоположный знак элементов матриц отвечает противофазному возбуждению плеч 1, 2 со стороны плеча 3. Действительно электрическое поле нормально к плоскости симметрии и касательная составляющая в плоскости симметрии равна нулю только при условии, что в плечах 1, 2 электрические поля противофазны рис. 3.5.а. Таким образом, матрица рассеяния Т - образного сочленения идентичных волноводов имеет вид

.

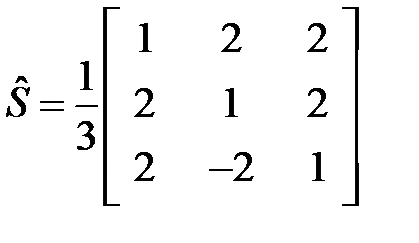Не нарушая симметрии сочленения его можно согласовать по плечу 3. В этом случае 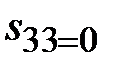. Это возможно, если волновое сопротивление плеча 3 равно 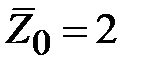. Волновое сопротивление волновода (1.29), (1.31) можно увеличить вдвое, если увеличить вдвое его высоту. В Т – образном сочленении это не изменит симметрии относительно плоскости. Положив 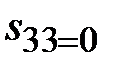из условия унитарности получим 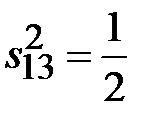. Следовательно, при согласовании плеча 3 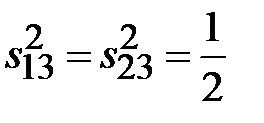и устройство делит мощность, поступающую в плечо 3 поровну между плечами 1 и 2 при этом сохраняется противофазное состояние в плечах 1 и 2, 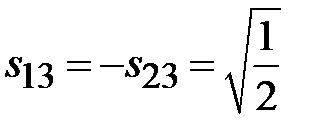. В согласованном тройнике сопротивление нагрузки в плоскости симметрии для горизонтальных плеч равно 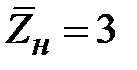, поэтому 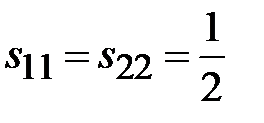. Из свойств унитарности получим, что 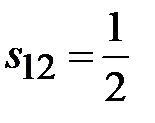. Таким образом, при согласовании плеча 3 матрица рассеяния имеет вид

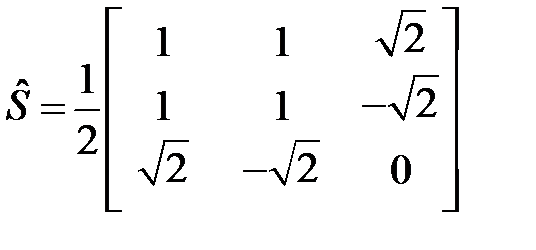. (3.21)

Запишем систему уравнений, связывающую падающие и рассеянные волны в Т – сочленении. В соответствии с (3.21) и (3.6) запишем

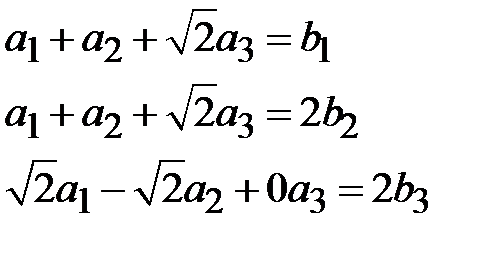. (3.22)

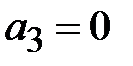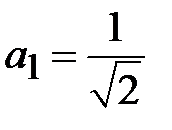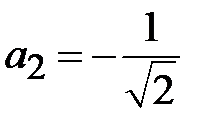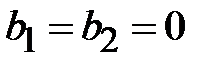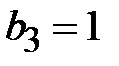Допустим, что в плечи 1 и 2 поступают противофазные поля с равными амплитудами, а плечо 3 подключено к согласованной нагрузке, то есть . Зададим , . Из (3.22) следует, что в этом случае , а . Таким образом, суммарная мощность двух плеч поступает в плечо три.

Допустим, что волновое сопротивление вертикального плеча 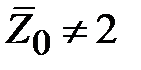и не равно волновым сопротивлениям горизонтальных плеч. Это возможно при разных размерах узких стенок плеч. В этом случае сопротивление нагрузки в плоскости симметрии для плеча 3 и плеч 1 и 2 будут разными и, следовательно, 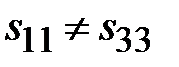, а из свойств унитарности следует, что .

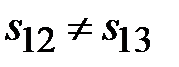Отметим еще одно важное свойство волноводного тройника: не нарушая симметрии его нельзя согласовать по первому и второму плечу, и по всем трем плечам. Если положить 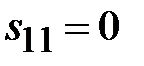, то из уравнения унитарности следует, что 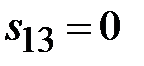, то есть вертикальный волновод не связан с горизонтальным. Если тройник считать согласованным по всем трем плечам, надо положить 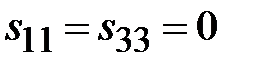. В этом случае, из унитарности матрицы рассеяния, следует 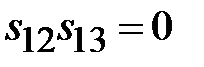, что приводит к отсутствию связи между всеми волноводами, образующими тройник.

3.4. Матрицы рассеяния Т и Y – образных тройников в H плоскости

Симметричные T, Y – волноводные сочленения, образованные пересечением волноводов в H плоскости, показаны на рис. 3.6. Если волноводы идентичны, то сочленения обладают симметрией относительно плоскости, а Y тройник имеет ось симметрии.

Найдем матрицу рассеяния Т – тройника, симметричного относительно плоскости отражения рис. 3.6.а. В этом случае тройник может быть образован волноводами с разной шириной широких стенок, что не нарушает симметрию относительно плоскости отражения. Матрицы рассеяния Т образных Е и Н тройников близки друг к другу. Действительно, матрица 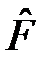, отвечающая операции отражения в плоскости симметрии Н тройника имеет вид

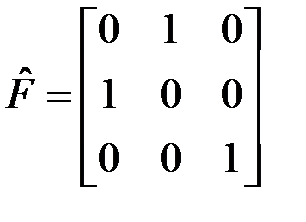. Поэтому матрица рассеяния Н тройника, удовлетворяющая условию коммутативности 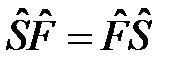, имеет вид

.

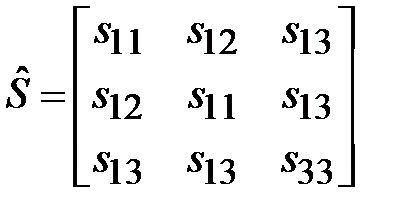Различие матриц рассеяния Т – образных Е и Н тройников состоит только в том, что в Н тройнике 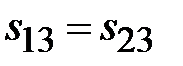и передача мощности из плеча 3 в плечи 1 и 2 происходит синфазными волнами. Из матрицы рассеяния следует, что в общем случае 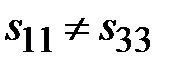. Матрица рассеяния Т тройника без потерь унитарна, что приводит к соотношениям между элементами матрицы

, .

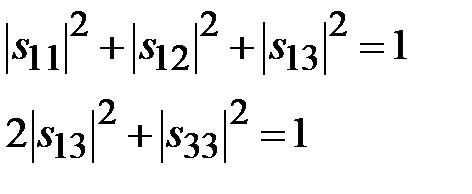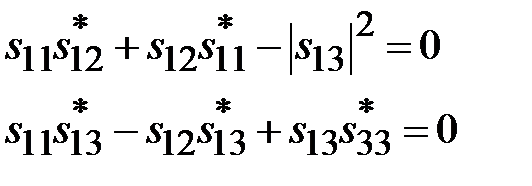Элементы матрицы рассеяния вещественны. Найдем элементы матрицы рассеяния тройника на основании эквивалентной схемы тройника. Эквивалентная схема сочленения приведена на рис. 3.7.

Она представляет собой шестиполюсник, образованный параллельным соединением трех линий передач. Сначала выполним расчет матрицы рассеяния Т тройника, образованного одинаковыми волноводами с 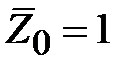. В этом случае каждое плечо тройника нагружено на нормированное сопротивление нагрузки в плоскости симметрии равное параллельному соединению двух волновых сопротивлений, то есть 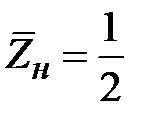, рис. 3.7.б. Поэтому, диагональные элементы матрицы рассеяния равны 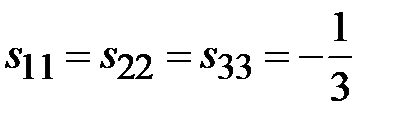. Из каждого плеча тройника в два других плеча поступают одинаковые мощности равные 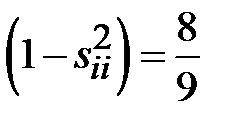и делятся поровну между соответствующими парами волноводов. Поэтому квадраты всех недиагональных элементов равны 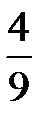, а сами элементы 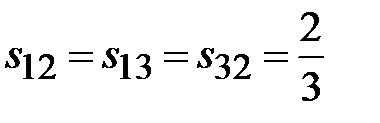. Таким образом, матрица рассеяния Т тройника образованного одинаковыми волноводами имеет вид

.

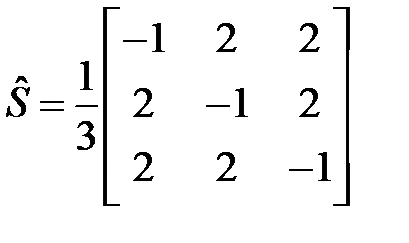Тройник в H плоскости во многом аналогичен E тройнику. Не нарушая симметрии, его можно согласовать со стороны плеча 3. Для этого надо обеспечить волновое сопротивление третьего плеча равное 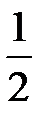. В этом случае 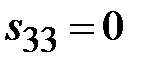и единичная мощность из третьего плеча разделится поровну между плечами 1 и 2. Это означает, что 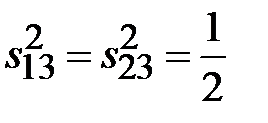и 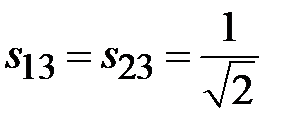. Плечи 1, 2 в плоскости симметрии нагружены на 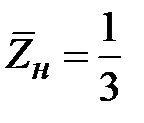, что определяется параллельным соединением волновых сопротивлений рис. 3.7.б. Поэтому два диагональных элемента матрицы, равные коэффициентам отражений от нагрузки 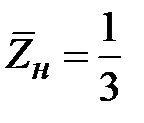равны 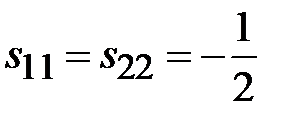. Из условия унитарности 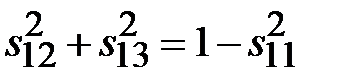, поэтому 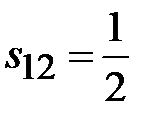. Таким образом, матрица рассеяния Т тройника в H плоскости при согласовании третьего плеча имеет вид

.

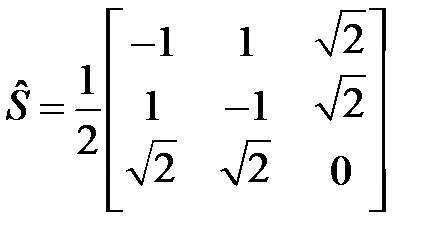Согласованный тройник представляет собой устройство синфазного деления мощности пополам (трех- децибельное деление) со стороны согласованного входа. Па аналогии с Е тройником одновременная передача синфазных полей в плечах один и два, приводит к суммированию их мощности в Н плече.

Тройник, образованный волноводами с разной шириной широких стенок имеет разные коэффициенты отражения по первому и третьему плечам, то есть 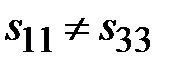. В такой конструкции сопротивление нагрузки плеча 3 и плеч 1 и 2 различны рис. 3.7.б. Тройник в Н плоскости нельзя согласовать по плечам 1 и 2, и одновременно по трем плечам. Это является общим свойством Е и Н тройников.

Найдем матрицу рассеяния Y образного тройника, образованного одинаковыми волноводами рис. 3.6.б., который имеет два вида симметрии: отражение в плоскости и поворот на 120⁰ вокруг оси симметрии. Очевидно, что матрица рассеяния Y тройника должна отвечать двум видам симметрии. Отражению в плоскости симметрии отвечает матрица рассеяния Т тройника, образованного одинаковыми волноводами

.

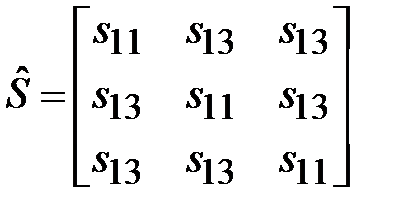К матрице 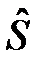надо применить соотношение коммутативности с оператором поворота вокруг оси. Из общих соображений ясно, что надо выбрать только поворот вокруг оси симметрии на 120⁰, так как последующий поворот на 240⁰ дает совпадающие результаты, а поворот на 360⁰ тривиален. Запишем оператор поворота 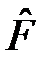на 120⁰ по часовой стрелке, который приводит к замене входов тройника: 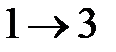, , 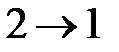, 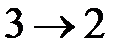поэтому 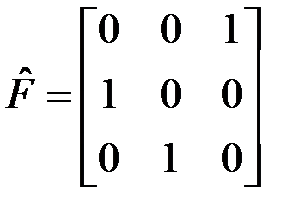. 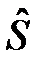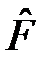Коммутативность матриц и приводит к соотношениям

,

.

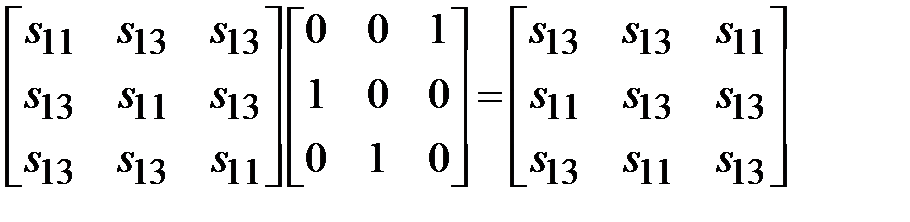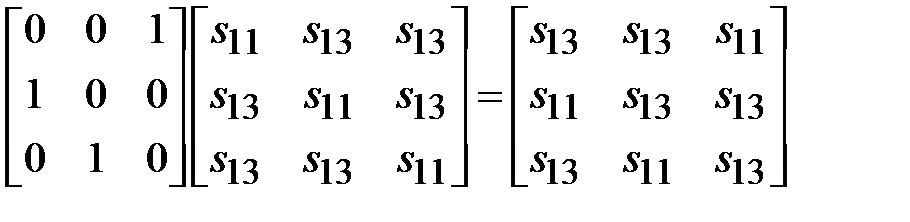Отсюда следует, что матрица рассеяния Y тройника совпадает с матрицей рассеяния Т тройника в Н плоскости, образованного одинаковыми волноводами.

3.5. Двойное Т сочленение

Конструктивное объединение Е и Н Т - тройников в единое волноводное устройство образует двойное Т или “магическое” Т сочленение, рис. 3.8.

Устройство симметрично относительно плоскости отражения. Оператор отражения имеет вид

.

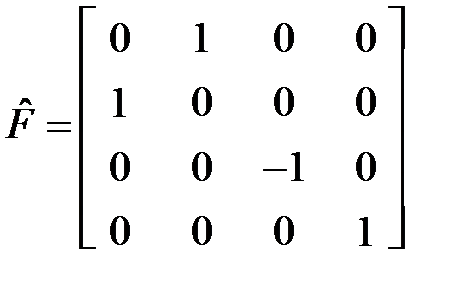Условие коммутативности матрицы рассеяния 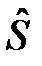двойного Т и матрицы 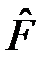приводят к соотношениям

,

.

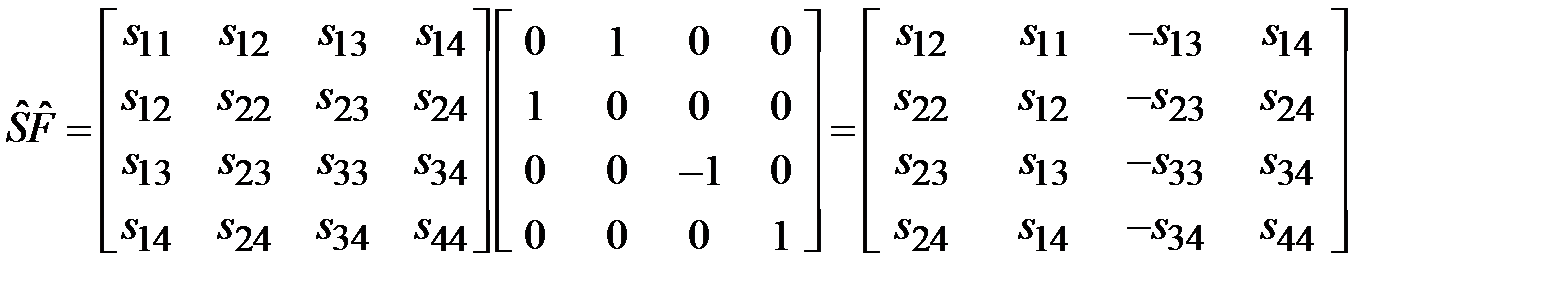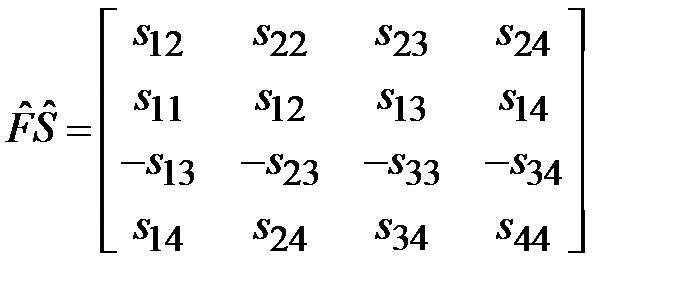Условие коммутативности выполняется, если 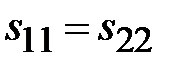, , 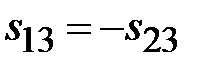, 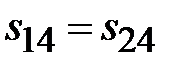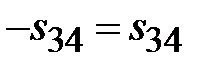. Последнее равенство возможно если 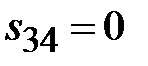: плечи 3 и 4 развязаны в силу ортогональности поляризации полей в волноводах 3 и 4 рис. 3.8. В предыдущих разделах было показано, что Е и Н тройники могут быть согласованы по Е и Н плечам. Рассмотрим матрицу рассеяния двойного Т соединения пологая, что оно согласовано по входам 3 и 4, то есть 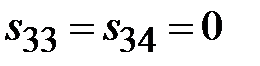. Тогда из свойства унитарности матрицы следует

.

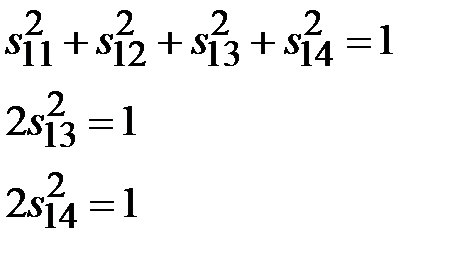Откуда найдем, что 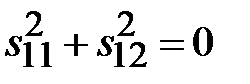. Это соотношение выполняется только при условии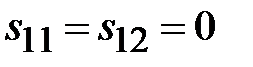

Таким образом, матрица рассеяния двойного Т сочленения согласованного по Е и Н плечам имеет вид

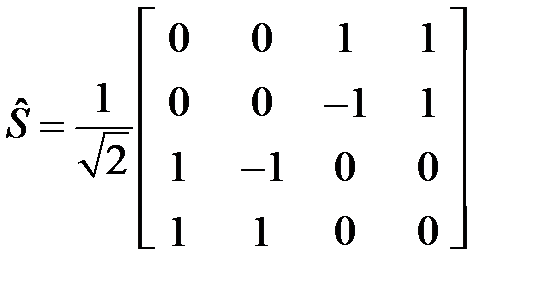. (3.23)

Запишем зависимость между падающими и рассеянными волнами, используя (3.23) в виде

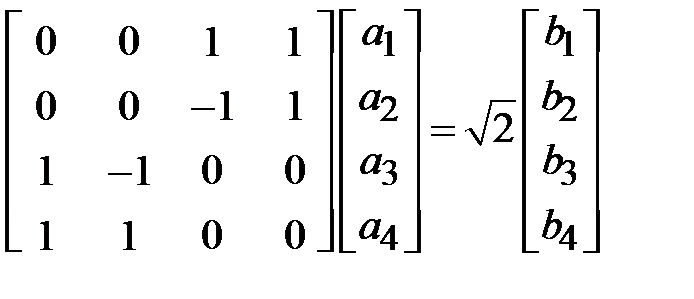. (3.24)

На основании правила перемножения матриц из (3.24) следует, что

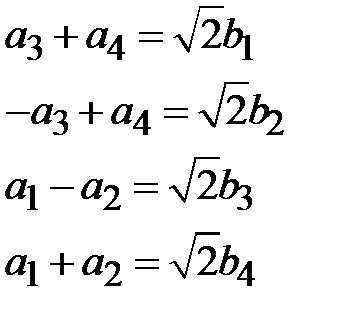. (3.25)

Из системы уравнений (3.25), следуют свойства двойного Т сочленения:

- мощность поступает в Н плечо, остальные плечи согласованы, тогда 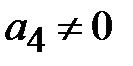, 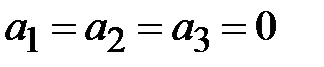. Из (3.25) следует, что 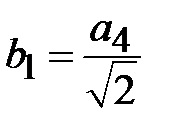, , 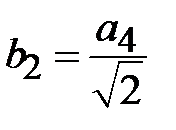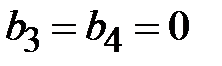. Следовательно, в этом режиме мощность, поступившая в Н плечо делится поровну между плечами 1 и 2.

- мощность поступает в плечо Е, остальные плечи согласованы, тогда 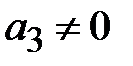, 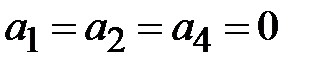. Из (3.25) следует, что 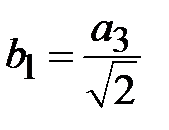, , 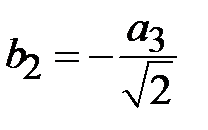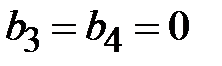. В этом случае, мощность поступившая в Е плечо делится поровну между плечами 1 и 2 при противофазном состоянии полей.

- мощность поступает в плечо 1, остальные плечи согласованы, тогда 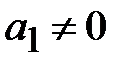, 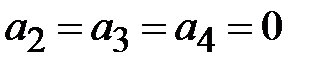. Из (3.25) следует, что 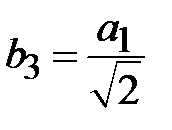, , 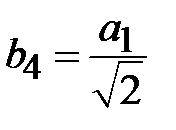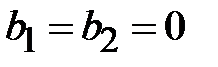. Таким образом, мощность делится поровну между Е и Н плечами при синфазном состоянии полей.

- мощность поступает в плечо 2, остальные плечи согласованы, тогда 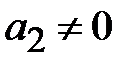, 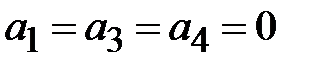. Из (3.25) следует, что 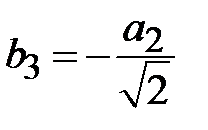, , 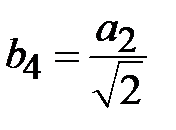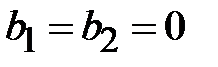. В этом случае, мощность делится поровну между плечами Е и Н при противофазном состоянии полей.

- в каналы 1 и 2 поступают равные мощности синфазных полей. Тогда, 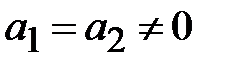, 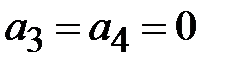. Из (3.25) следует, что 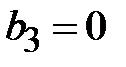и суммарная мощность обоих плеч поступает в Н плечо.

- в каналы 1 и 2 поступают равные мощности противофазных полей. Тогда, 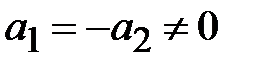, , 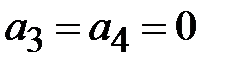тогда из (3.25) следует, что 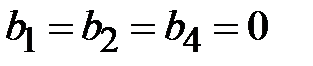и суммарная мощность обоих плеч поступает в Е плечо.

- По аналогии с предыдущими пунктами, можно сделать два дополнительных вывода: при поступлении в плечи Е и Н равных синфазных полей их суммарная мощность, поступает в плечо 1; при равных противофазных полях в Е и Н плечах мощность поступает в плечо 2.

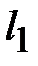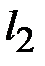Рассмотрим свойства двойного Т сочленения при несогласованных плечах. Допустим, что в плечах 1 и 2 на расстояниях равных и от плоскости симметрии, помещены коротко-замыкающие поршни рис. 3.9. Мощность из Н плеча делится поровну между плечами 1 и 2. Поля в первом и во втором плечах будут синфазны и равны по амплитуде. При отражении от к.з. поршней с коэффициентом отражения равным -1 в плоскости симметрии возникают поля

, ,

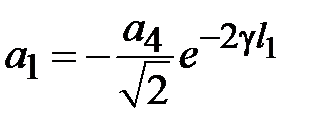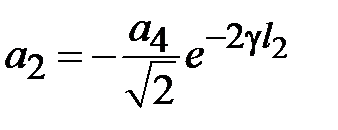где 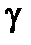- постоянная распространения в волноводах.

В соответствии с (3.25) в плечах Е и Н возникнут рассеянные волны

,

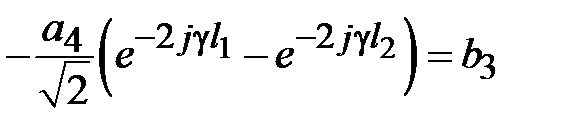(3.26)

.

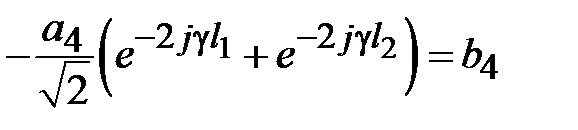Преобразуем (3.26), вынеся в обоих уравнениях общий множитель 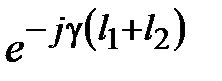, получим

,

.

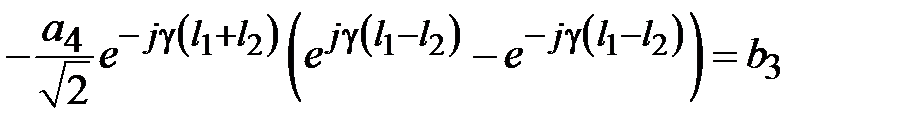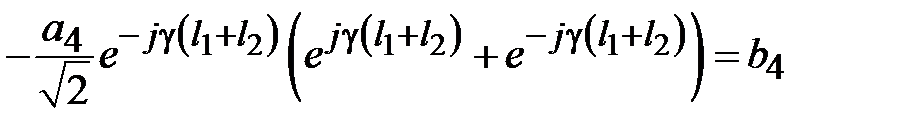Выражения, стоящие в скобках, можно привести с помощью формул Эйлера к виду

,

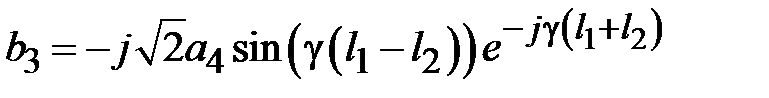(3.27)

.

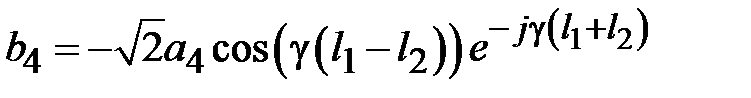Мощность 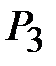, поступающая в Е плечо, пропорциональна квадрату модуля 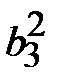. Поэтому на основании (3.27) получим, что

.

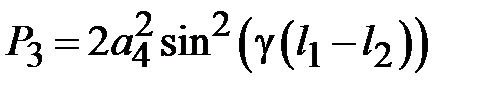Мощность, отраженная в Н плечо, пропорциональна квадрату модуля 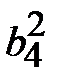, поэтому

.

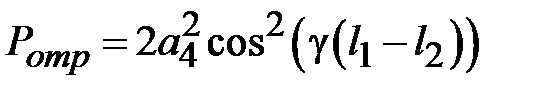Из этих соотношений следует, что при 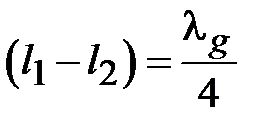вся мощность, поступившая в Н плечо, без отражения поступает в Е плечо.

Рассмотренная схема включения двойного Т сочленения с к.з. поршнями, используется для построения антенного переключателя радиолокационной станции (РЛС), работающей в импульсном режиме на одну антенну. Антенна подключена к Е плечу, передатчик к Н плечу. Роль к.з. поршней выполняют полупроводниковые диоды, которые включены параллельно в волноводах один и два. Подача управляющего напряжения на диоды переводит их в состояние “открыто”, что близко к к.з. в месте расположения диодов, синхронизована с работой передатчика станции. Поэтому в течении времени работы передатчика его мощность поступает в Е плечо. В течении времени работы РЛС на “прием”, с диодов снято управляющее напряжение, и волноводы оказываются близки к режиму холостого хода. Поэтому сигнал с антенны поступает в Е плечо, и делится поровну между первым и вторым плечами.

3.6. Волноводные направленные ответвители

Волноводные направленные ответвители (НО), образованы четырьмя одинаковыми волноводами, которые связаны между собой отверстиями в общей широкой или узкой стенками волновода. Условная схема многодырочного НО представлена на рис. 3.12, в котором отверстия связи расположены симметрично относительно плоскости симметрии. Это означает, что симметрично расположенные отверстия одинаковы по форме и размерам. В общем случае элементы матрицы рассеяния симметричного восьмиполюсника подчиняются соотношениям

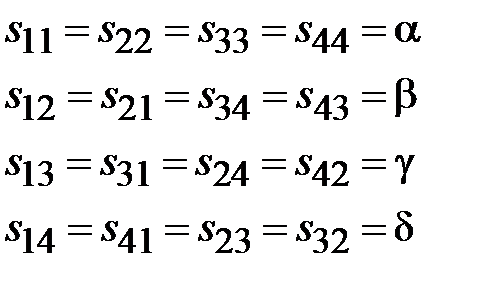
НО “ответвляет” заданный уровень мощности только в канал, расположенный по направлению распространения волны. Поэтому “идеальный” НО должен быть согласован по всем входам, а каналы 1, 3 и 2, 4 должны быть развязаны. Таким образом, у идеального направленного ответвителя 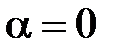, 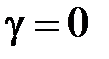и матрица рассеяния НО имеет вид

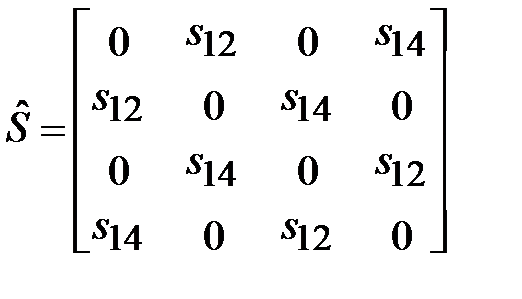. (3.28)

Матрица рассеяния унитарна, что выражается в уравнениях связи между ее элементами

.

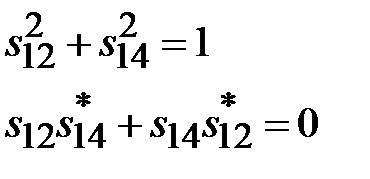Таким образом, связь между каналами 1 и 2, 3 и 4 одинакова, а связь между каналами 1 и 4 равна связи между каналами 2 и 3. Следовательно, мощность ответвляющаяся из канала 1 в канал 4, равна мощности, ответвляющейся в канал 3 из канала 2. Фазовые соотношения между элементами матрицы могут быть произвольными. Основными параметрами НО являются: переходное ослабление 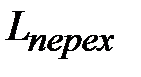и направленность 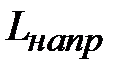. Переходное ослабление определяется соотношением

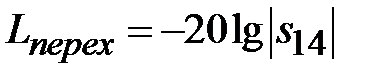. (3.29)

Направленность, характеризует приближение НО к идеальному, и определяется соотношением

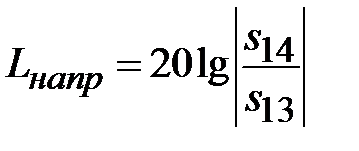. (3.30)

При “идеальной” направленност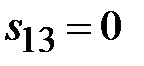и и 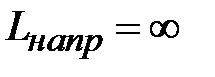. Поэтому чем выше направленность ответвителя, тем выше его качество. Значение переходного ослабления, определяется назначением НО и может лежать в широких пределах. Оба параметра определяются электродинамической связью между волноводами НО. На рис. 3.11 показана многодырочная связь через малые отверстия в общей широкой или узкой стенках волноводов. Отверстия расположены симметрично на одинаковых расстояниях равных 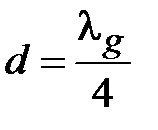. Отверстия малы, поэтому их излучение можно считать ненаправленным. Это означает, что волны возбуждаемые отверстиями в связанном волноводе в противоположных направлениях равны по амплитуде. Обозначим амплитуды возбуждаемых волн как 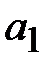, ,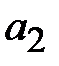.., , 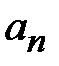где индекс обозначает номер отверстия связи. Волны, распространяющиеся в связанном волноводе, в прямом и обратном направлениях, определяются суперпозицией волн, возбуждаемых отверстиями связи. Тогда результирующая волна обратного направления в клеммной плоскости 3 при единичной мощности в падающей волне равна элементу матрицы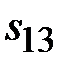

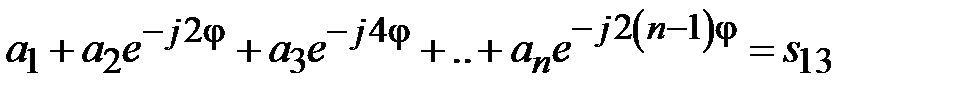, (3.31)

где 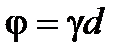- фазовый набег, приобретаемый волнами на расстоянии между отверстиями. В соотношении (3.31) показатели экспонент равны фазовым сдвигам приобретаемым волнами от каждого отверстия связи в месте расположения первого отверстия. На рабочей частоте 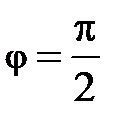, поэтому (3.31) преобразуется к виду

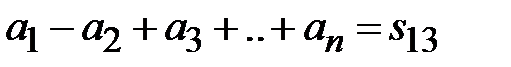. (3.32)

Как видно, волны возбуждаемые отверстиями связи, складываются в клеммной плоскости в противофазе и при соответствующем выборе значений амплитуд, можно обеспечить требуемый минимум амплитуды волны, распространяющемся в обратном направлении. Тем самым на входе сохраняется значение коэффициента отражения той же величины

Результирующая амплитуда волны в связанном волноводе, распространяющейся в прямом направлении будет определяться, синфазным сложением волн, в клеммной плоскости 4

.

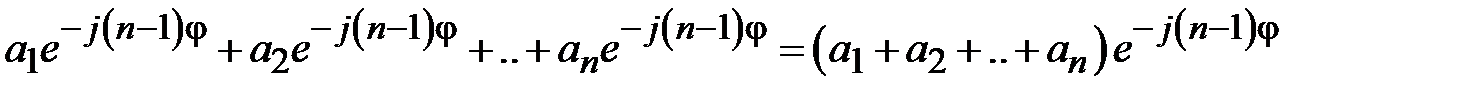При единичной мощности в падающей волне имеем

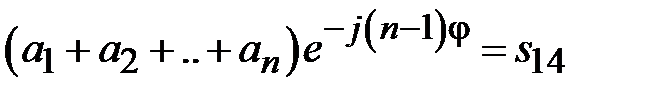. (3.33)

Расчет НО состоит в получении требуемой направленности и переходного ослабления. С этой целью надо задать распределение значений амплитуд волн, возбуждаемых отверстиями связи. В качестве примера выберем биномиальное распределение на пяти отверстиях связи. При 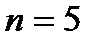амплитуды возбуждаемых волн будут пропорциональны амплитуде волны возбуждаемой первым отверстием. В соответствии с биномиальным распределением (раздел 2.4) 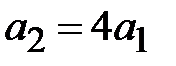, , 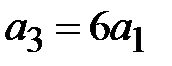, 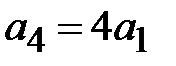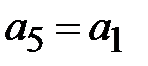. Зададим переходное ослабление -20Дб, что означает 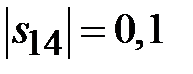. В этом случае из (3.32) следует, что на рабочей частоте 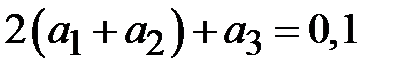. Отсюда при биномиальном распределении имеем, что 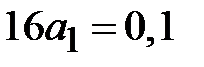и , , . 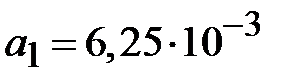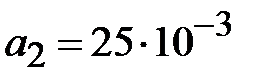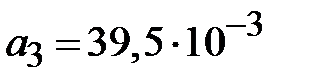Направленность на рабочей частоте, очевидно, равна бесконечности, так как из (3.32) следует, что 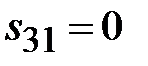. Качество НО определяется сохранением требуемых значений двух основных параметров в заданной полосе частот.

4. ОБЪЕМНЫЕ РЕЗОНАТОРЫ

4.1. Электромагнитные поля в объемных резонаторах

Объемные резонаторы, представляют собой отрезки волноводов или линий передачи с металлическими стенками в торцах. Вид волновода определяет вид резонатора: прямоугольный, круглый цилиндрический, коаксиальный. В замкнутом объеме электромагнитное поле может существовать только в виде колебаний. Поэтому надо установить условия при которых возможно возникновение колебаний в замкнутом объеме. Электромагнитные колебания в объеме вне связи с источником возбуждения называются свободными или собственными колебаниями. Связь резонатора с источником возбуждения создает вынужденные колебания. Рассмотрим условия возникновения собственных колебаний. На рис. 4.1 изображен отрезок волновода произвольного поперечного сечения длинною l, короткозамкнутый по направлению распространения волны. В волноводе с идеально проводящими стенками могут существовать Н и Е волны. Поперечные компоненты Н волн определяются через продольную компоненту магнитного поля как

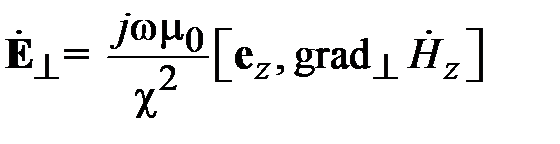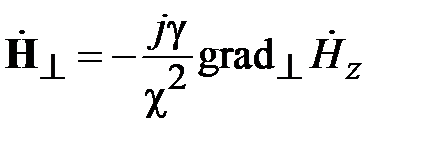, . (4.1)

Поперечные компоненты Е волн определяются через продольную компоненту электрического поля

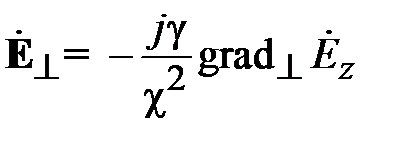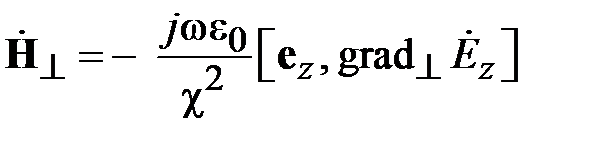, . (4.2)

В этих соотношениях 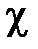– поперечное волновое число, известное из раздела 1. Зависимость полей волновода от z определяется экспоненциальным множителем 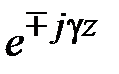. В замкнутом объеме электромагнитное поле может существовать только в виде волн отраженных от к.з. торцов и распространяющихся в противоположных направлениях. Эти волны идентичны на поперечном сечении. Поэтому поперечный вектор результирующего электрического поля в резонаторе можно представить в виде

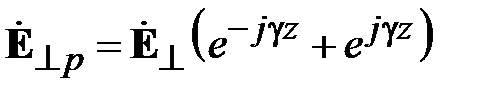. (4.3)

Поперечный вектор напряженности электрического поля (4.3), касателен к торцам волновода и, следовательно, обращается в ноль на их поверхностях. При 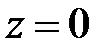поперечный вектор 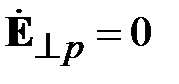при условии, что слагаемые в (4.3) имеют разные знаки, поэтому (4.3) преобразуется к виду

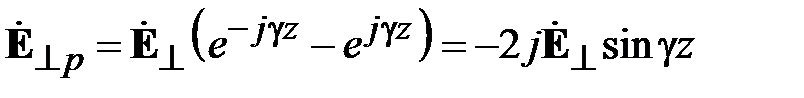. (4.4)

При 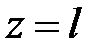поперечный вектор 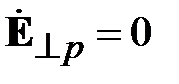, что приводит к уравнению 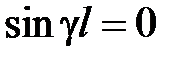, откуда

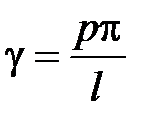, (4.5)

где .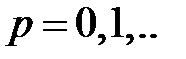

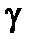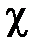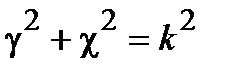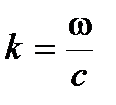Постоянные распространения и связаны между собой соотношением , где . Значения 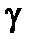и 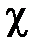дискретны, поэтому электромагнитное поле в объемном резонаторе существует только на дискретных частотах, определяемых соотношением 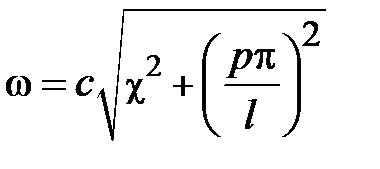. Эти частоты называются резонансными или собственными частотами резонатора. Например, резонансные частоты прямоугольного резонатора, образуют ряд дискретный значений,

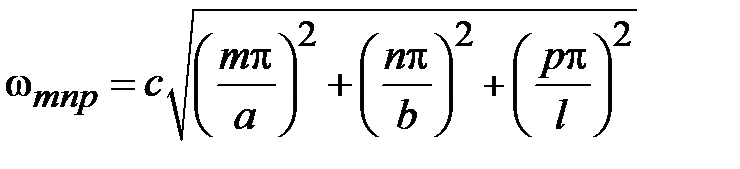. (4.6) а поля резонатора магнитного и электрического типа обозначаются как ,

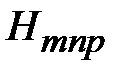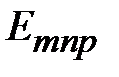
На резонансных частотах длина резонатора в соответствии с (4.5) кратна половине длине волны в волноводе 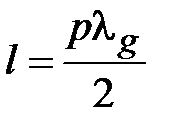. Значение 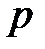может быть равно нулю и это не противоречит граничному условию на торцах волновода. Однако, для Н колебаний случай 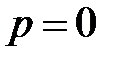( 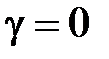) не имеет физического смысла, так как в соответствии с (4.1) в объеме резонатора 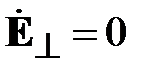, что равносильно обращению в нуль 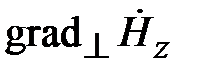, это противоречит граничному условию для нормальной составляющей напряженности магнитного поля на идеально проводящей поверхности. Следовательно, электромагнитное поле 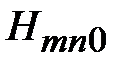в цилиндрических резонаторах не существует. Для Е волн при 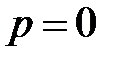( 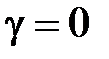) равенство нулю поперечного вектора 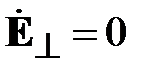отвечает граничному условию на торцах резонатора 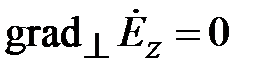. Однако, в этом случае, длина резонатора становится неопределенной, так как в соответствии с (4.5) 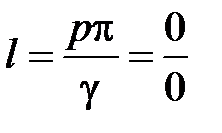, и следовательно, резонанс возможен при любой длине резонатора. Таким образом, резонансные частоты 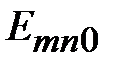типов колебаний цилиндрических резонаторов равны 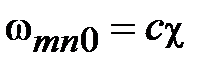, а в структуре поля 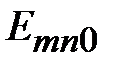отсутствуют поперечные составляющие электрического поля (4.2).

Для нахождения полей в объемных резонаторах, преобразуем соотношения (4.1) и (4.2). Эти соотношения получены для волноводов при условии зависимости электромагнитного поля от оси 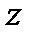в виде 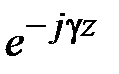. Дифференцирование по 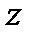равносильно умножению на 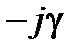, поэтому, при вычислении полей объемных резонаторах в соотношениях (4.1) и (4.2) надо заменить 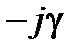на производную 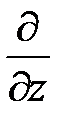. Таким образом, для объемных резонаторов связь между поперечными и продольными составляющим можно представить в виде:

- для Е полей

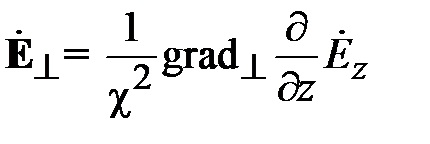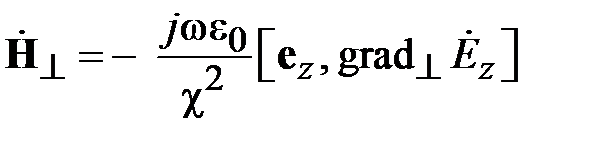, . (4.7)

- для Н полей

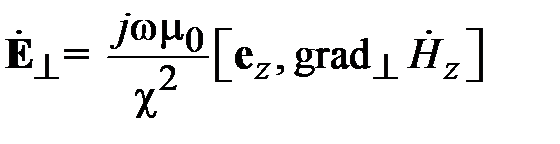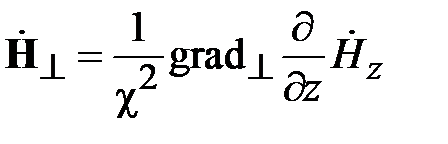, , (4.8)

Дифференцирование по 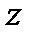в соотношениях (4.7), (4.8) не меняет фазовый сдвиг между электрическим и магнитным полем. Поэтому между ними сохраняется фазовый сдвиг во времени 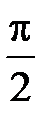. Таким образом, поле резонатора имеет колебательный характер: в момент максимального значения магнитного поля, электрическое поля равно нулю и наоборот.

4.2. Собственная добротность объемных резонаторов

Возможность существования электромагнитного поля на дискретных частотах возможно только при условии идеально проводящих стенок резонатора. Это в свою очередь означает, что собственное колебание, возникшее в резонаторе, будет существовать бесконечно долго. Очевидно, это противоречит закону сохранения энергии, согласно которому, энергия электромагнитного поля в замкнутом объеме должна релаксировать к нулю, обращаясь в тепловую энергию. Скорость релаксации энергии определяется собственной добротностью резонатора на резонансной частоте, определяемую как

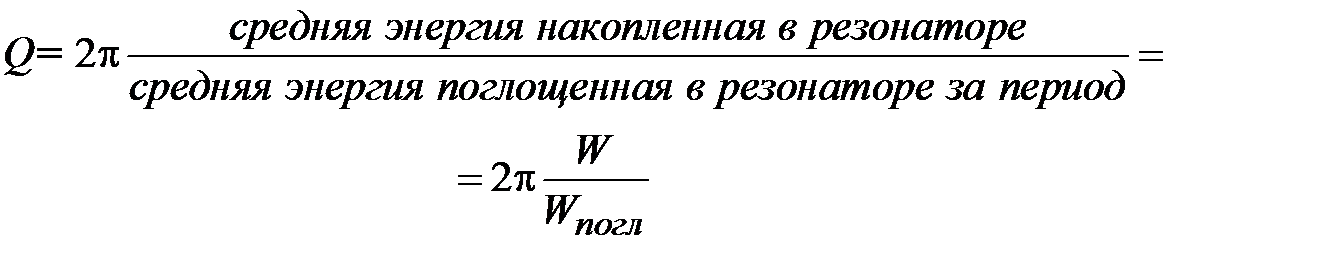. (4.9)

Множитель 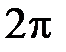введен для окончательного упрощения вида формулы. Соотношение (4.9) можно преобразовать к иному виду, заменив поглощенную за период энергию, мощностью потерь через соотношени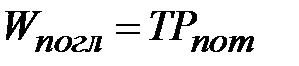е , где 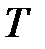- период колебания на резонансной частоте 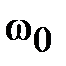. Поэтому (4.9) в эквивалентной форме есть

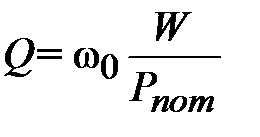. (4.10)

Согласно закону сохранения энергии, мощность потерь определяется скоростью уменьшения накопленной энергии, то есть

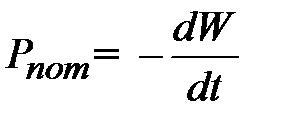. (4.11)

Объединив (4.10) и (4.11) в общее соотношение, получим

.

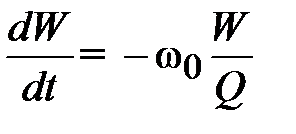Решение этого уравнения, определяет экспоненциальный спад накопленной энергии

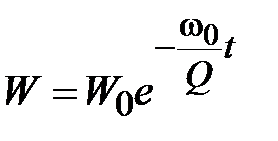. (4.12)

Электромагнитное колебание, возникшее на частоте резонанса, будет затухать по амплитуде. Квадратичная зависимость энергии от амплитуды колебания, позволяет представить напряженность электрического поля в резонаторе в соответствии с (4.12) в виде

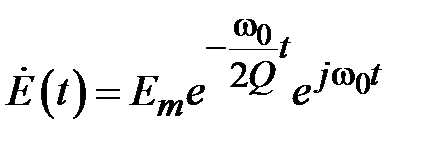. (4.13)

Колебание, непрерывно изменяющееся во времени, имеет спектральную плотность 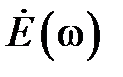, которая вычисляется прямым преобразованием Фурье от 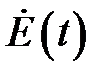. Таким образом

.

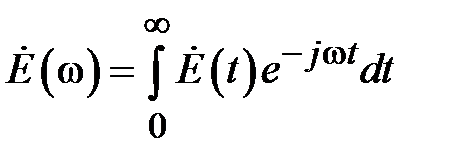Подставим в это соотношение (4.13), получим

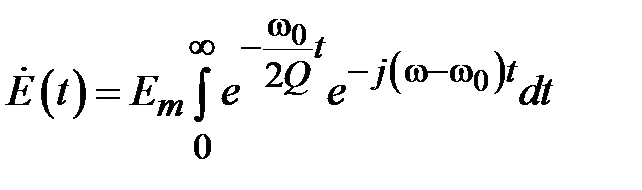. (4.14)

Интеграл в (4.14) вычисляется точно, поэтому

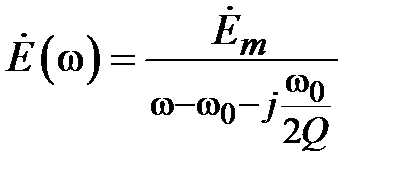. (4.15)

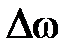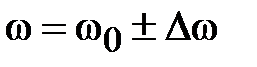Следуя анализу резонансных систем, введем малую расстройку , как , где 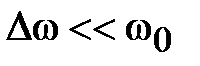. Тогда (4.15) можно преобразовать к виду

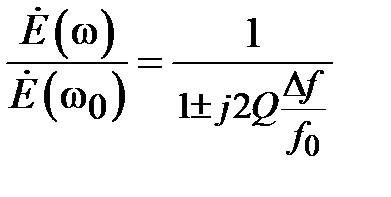, (4.16)

где 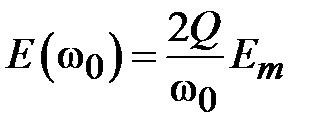- значение спектральной плотности на резонансной частоте.

Квадрат модуля соотношения (4.16) представляет нормированную частотную зависимость энергии накопленной в резонаторе. Из (4.15) найдем

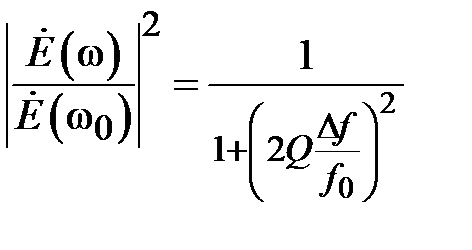. (4.17)

Соотношение (4.17) точно совпадает с частотной характеристикой LC колебательных контуров. Расстройка частоты 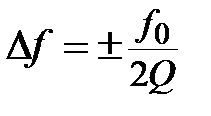соответствует спаду энергии до уровня равного 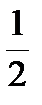. Полоса частот, соответствующая половинному спаду энергии равная 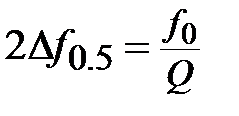называется полосой пропускания объемного резонатора.

4.3. Численная оценка собственной добротности резонаторов

Накопленная энергия в объемном резонаторе есть интеграл от объемной плотности энергии 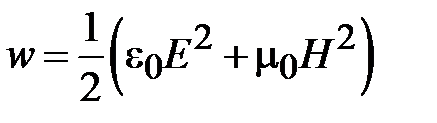. Объемную плотность энергии можно взять в момент времени соответствующему либо максимуму электрического поля (напряженность магнитного поля в этот момент равна нулю), либо максимуму магнитного поля (напряженность электрического поля равна нулю). Поэтому запишем среднюю накопленную энергию как

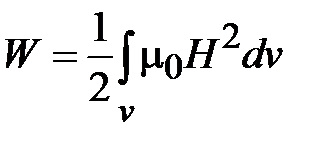. (4.18)

Среднюю мощность потерь, найдем как интеграл по площади стенок резонатора от мощности потерь на глубине скин слоя. Ток в скин слое является поверхностным током 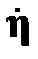(1.4), поэтому мощность потерь определяется как

,

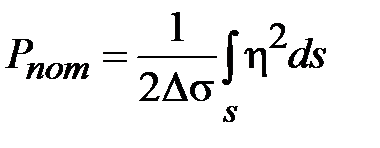где - глубина скин слоя (1.3).

В соответствии с граничными условиями на проводящей поверхности, поверхностный ток 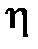равен касательному магнитному полю 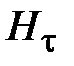на поверхности стенок резонатора, поэтому

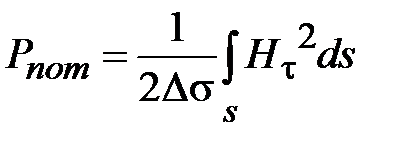. (4.19)

На основании (4.10), (4.18), (4.19) и (1.3) получим формулу для расчета собственной добротности резонатора

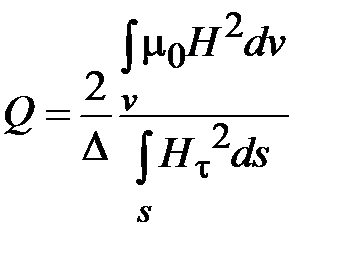. (4.20)

Найдем численную оценку собственной добротности на основании (4.20). Допустим, что магнитное поле в объеме резонатора и на его стенках распределено равномерно. Тогда интеграл в числителе (4.20) равен объему резонатора, а в знаменателе площади поверхности стенок, то есть

.

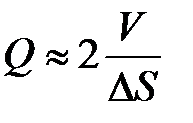Произведение 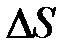можно считать равным объему резонатора, в котором происходит поглощение энергии. Таким образом, можно считать, что собственная добротность резонатора равна отношению его объема к объему, в котором происходит поглощение энергии. Объем круглого цилиндрического резонатора диаметром 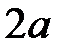и длинной равен 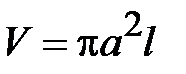, а площадь поверхности 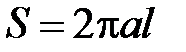. Поэтому численную оценку значения добротности круглого резонатора можно получить из соотношения 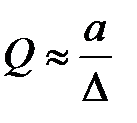. В свою очередь радиус цилиндра пропорционален длине волны, поэтому окончательно имеем 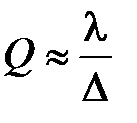. Отсюда следует, что на длине волны мм собственная добротность резонатора выполненного из меди теоретически оценивается по порядку величины .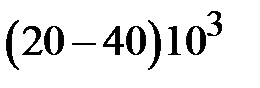

4.4. Объемные резонаторы прямоугольной формы

Рассмотрим Е поля резонатора, образованного отрезком прямоугольного волновода с размерами 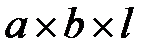. Продольная составляющая электрического поля на торцах резонатора должна удовлетворять граничному условию как нормальная составляющая электрического поля на идеально проводящей поверхности, то есть 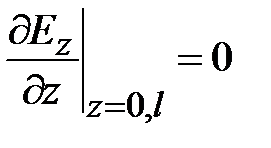. Поэтому на основании известной из теории волноводов зависимости 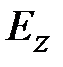от поперечных координат, имеем

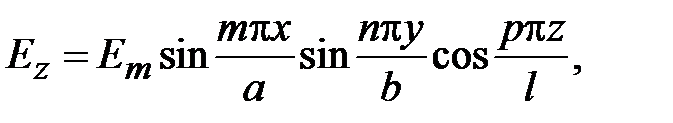
где .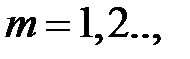

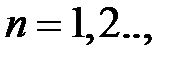
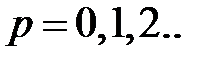Поперечные составляющие полей Е типа от поперечных координат определяются соотношением (4.7). Найдем, что

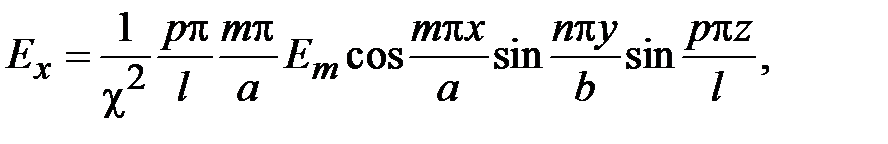
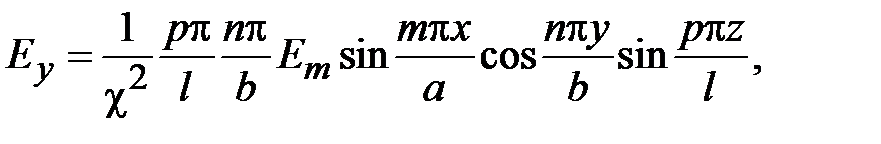
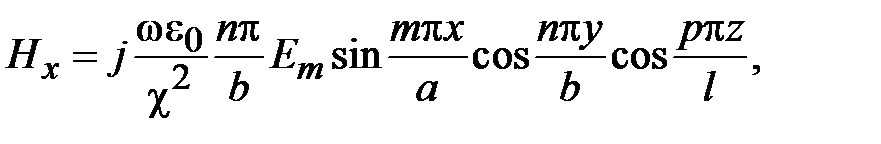
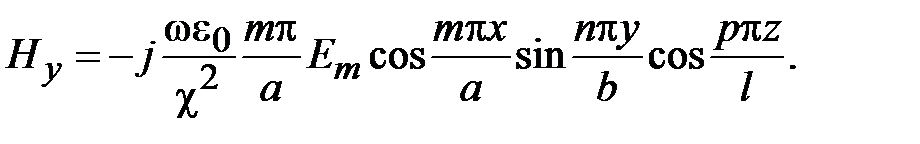
Рассмотрим Н поля резонатора. Продольная составляющая магнитного поля на торцах резонатора должна обращаться в ноль, как нормальная составляющая напряженности магнитного поля на идеально проводящей поверхности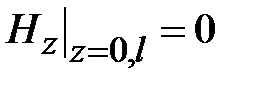

Поэтому на основании известной из теории волноводов зависимости 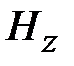от поперечных координат, имеем

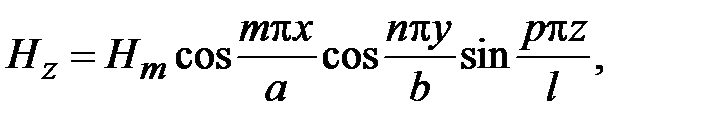
где .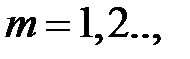

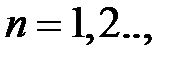
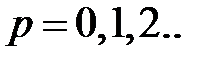Поперечные составляющие полей Н типа от поперечных координат определяются соотношением (4.8). Найдем, что

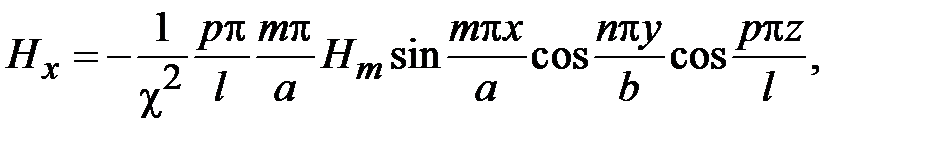
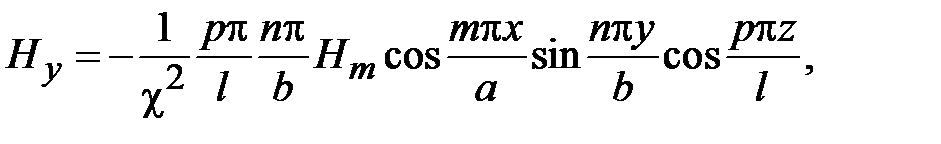
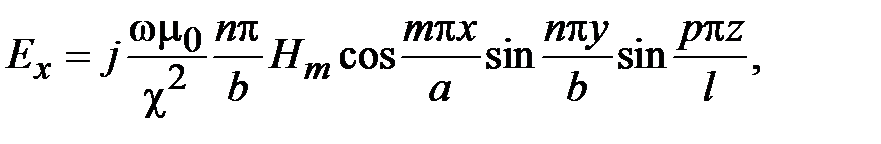
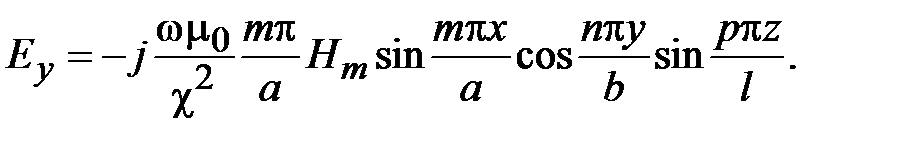
Собственные частоты резонансных колебаний полей Е и Н типов определяются соотношением (4.6). Любая комбинация чисел 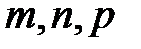, из которых ни одно не равно нулю, определяет равные собственные частоты колебаний Е и Н типов прямоугольных резонаторов. Один из индексов 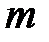или 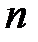для Н полей может быть равен нулю. Индекс 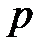может быть равен нулю для Е полей. Выбор продольной координаты в прямоугольном резонаторе может быть произвольным. Поэтому соотнесение собственных частот 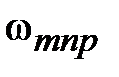типу колебания должно быть связано с ориентацией осей. Например, поле 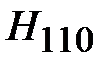в прямоугольном резонаторе с ориентацией: 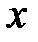- вдоль ребра широкой стенки, 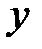- вдоль ребра узкой стенки, может совпадать с полям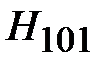и или 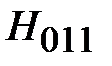при соответствующем изменении ориентации осей.

4.5. Цилиндрические круглые резонаторы

Круглый цилиндрический резонатор образован короткозамкнутым отрезком круглого волновода длины . Для полей Е типа в соответствии с граничными условиями на торцах резонатора, продольную составляющую электрического поля запишем в ви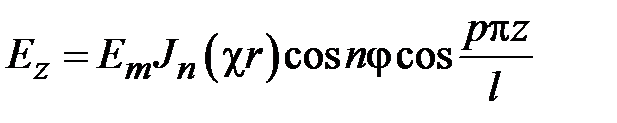де

, где 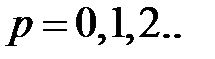. Поперечная постоянная 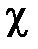определяется из уравнения (1.10) 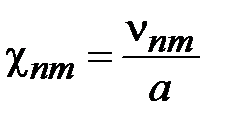. Поэтому собственные частоты цилиндрических резонаторов с Е полями равны 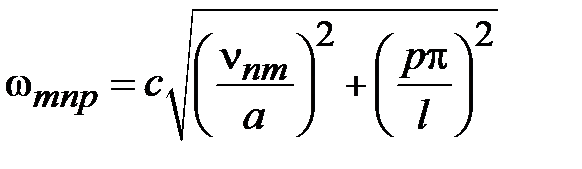. Низшему колебанию 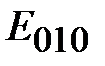отвечает низшее значение корня равное 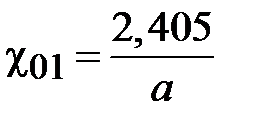, а низшее значение резонансной частоты

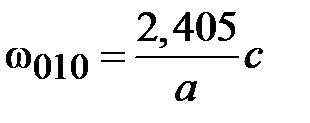. (4.21)

Из соотношения (4.7) найдем поперечные составляющие полей Е типа в круглых цилиндрических резонаторах

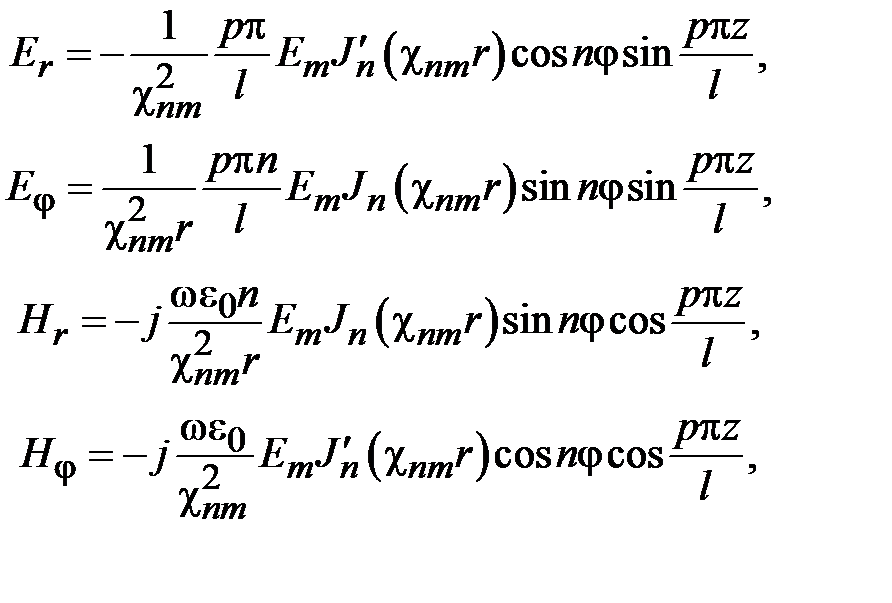
где .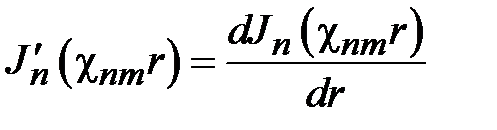

Продольную составляющую магнитного поля для Н типов колебаний с учетом граничного условия на торцах, запишем в виде 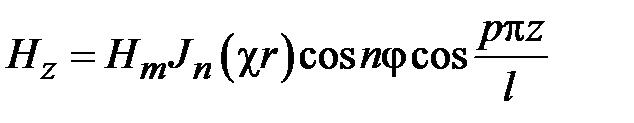, 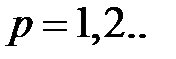. Поперечная постоянная 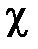определяется из уравнения 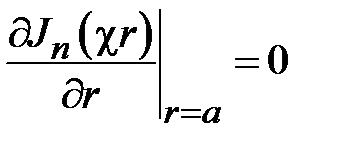. Обозначим корни этого уравнения как 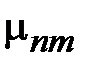где m - номер корня в бесконечной последовательности корней уравнения. Минимальное значение имеет первый корень при n=1, который отвечает основной волне Н₁₁, поэтому 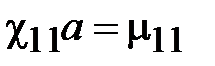, где . Таким образом, низшее значение резонансной частоты колебания 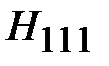типа равно

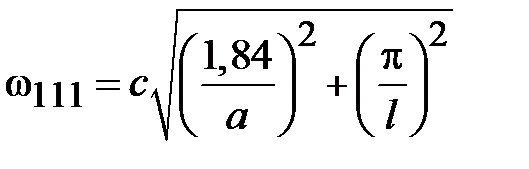. (4.22)

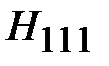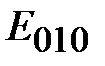Следовательно, низшими колебаниями круглого цилиндрического резонатора являются колебания и . Длина резонатора с колебанием 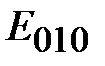типом не определена и его резонансная частота не зависит от . Однако, длину резонатора можно выбрать так, чтобы обеспечить равенство резонансных частот колебани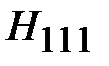й и 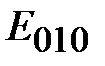. Для этого приравняем (4.21) и (4.22), получим уравнение

.

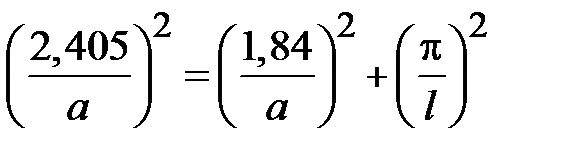Корень этого уравнения равен 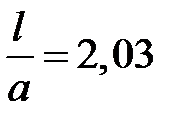. Поэтому, для “длинного” цилиндра с 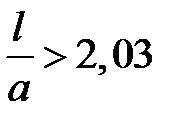основным колебанием является 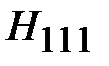, а для “короткого” цилиндра 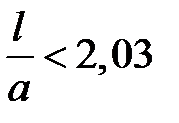низшим колебание является .

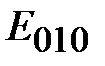4.6. Квазистационарные объемные резонаторы

Рассмотрим объемные резонаторы, конструкции которых приближаются к LC колебательным системам. Электрическое поле в них сосредоточено в узких зазорах, которые можно рассматривать как плоские конденсаторы, а окружающие их объемы играют роль индуктивности. Поэтому собственные частоты квазистационарных резонаторов можно вычислить как .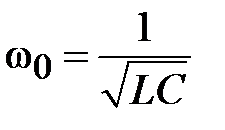

Рассмотрим два примера конструкций квазистационарных резонаторов.

Тороидальный резонатор. На рис. 4.2. представлено поперечное сечение прямоугольного тороидального резонатора. Электрическое поле резонатора сосредоточено в зазоре высотой 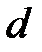, который можно рассматривать как конденсатор колебательной системы, емкость которого равна 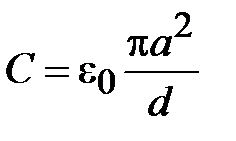. Магнитное поле сосредоточено в объеме тора. Оно создано током центрального цилиндра и равно 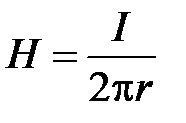. Поток магнитной индукции 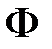, пронизывающий площадь 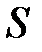поперечного сечения тороидальной области, равен 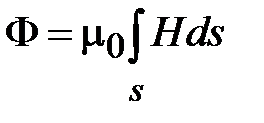. Элемент интегрирования, равен 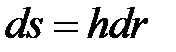, поэтому

.

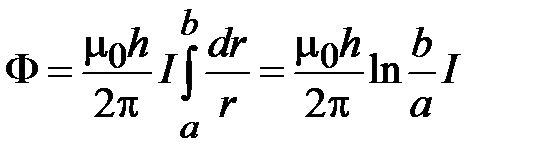Индуктивность 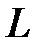есть коэффициент пропорциональности между током и потоком, поэтому находим, что

.

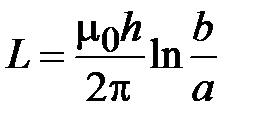Таким образом, резонансная частота тороидального резонатора равна

.

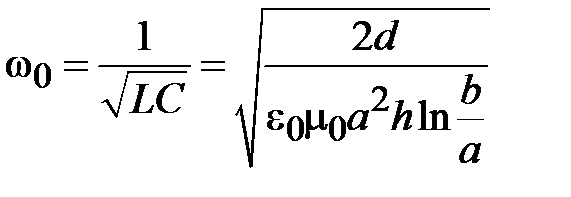При выборе соответствующих размеров резонатора резонансная частота лежит в области сверхвысоких частот.

Коаксиальный резонатор с емкостным зазором рис. 4.3.

Условие резонанса колебательной системы, определяется равенством реактивных сопротивлений на резонансной частоте. Если длина резонатора меньше четверти длины волны в линии, то в плоскости емкостного зазора эквивалентное сопротивление имеет индуктивный характер и уравнение резонанса имеет вид

.

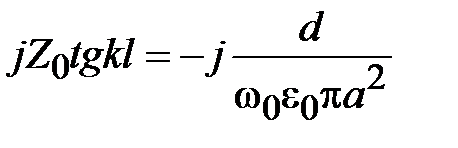Решением этого уравнения, является значение резонансной частоты.

4.7. Объемные резонаторы в вынужденном режиме

Связь объемного резонатора с генератором и нагрузкой, осуществляется различными техническими приемами. С этой целью используют диафрагмы индуктивного или емкостного типа, малые отверстия в стенках резонатора и др. Элементы связи неизбежно приводят к излучению накопленной энергии резонатором во внешнюю цепь и, следовательно, к ее потерям. Поэтому в вынужденном режиме возникает новый вид потерь, который зависит от вида связи резонатора с внешней цепью. Обозначим 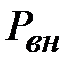- мощность потерь резонатора, передаваемую во внешнюю цепь. Тогда суммарная мощность потерь может быть представлена как

.

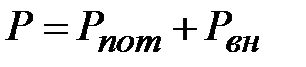Разделение потерь мощности в резонаторе на две составляющие, является условным, так как они между собой взаимосвязаны. Потери в стенках резонатора изменяют распределение поля, и, тем самым, изменяются условия связи резонатора с внешней цепью. И, наоборот, элемент связи изменяет поле в резонаторе, и, тем самым, изменяет омические потери. Однако, при условии малых потерь, что справедливо во всех практических случаях, можно пренебречь влиянием потерь на поле в резонаторе, считая, что оно сохраняется неизменным собственным полем. Это дает возможность рассчитать потери мощности и запасенную энергию независимо друг от друга, полагая неизменным поле в резонаторе. В этом предположении резонатор в вынужденном режиме можно характеризовать двумя видами добротности: собственной добротностью 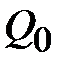и внешней добротностью 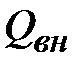, которые определяют нагруженную добротность 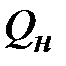. Представим 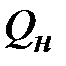в виде

.

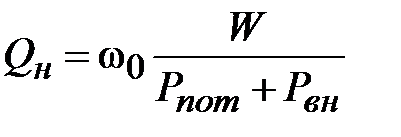Отсюда следует, что

,

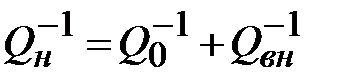где , .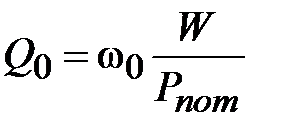

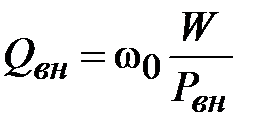Расчет мощности, отдаваемой резонатором во внешнюю цепь, можно выполнить только для конкретного вида связи резонатора с внешней цепью. Элементу связи всегда можно соотнести эквивалентную реактивную проводимость или сопротивление. Представив объемный резонатор в виде эквивалентной колебательной 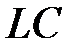цепи, можно простым расчетом учесть влияние элемента связи. Это влияние проявится в изменении реактивного сопротивления колебательной 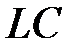цепи и, следовательно, в изменении резонансной частоты, а вносимое связью активное сопротивление увеличит потери резонатора. Таким образом, при условии эквивалентного представления объемного резонатора и элементов связи в виде единой колебательной 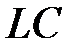цепи, можно рассчитать мощность, теряемую во внешней цепи, как мощность, поглощаемую активным сопротивлением, вносимым в контур.

Рассмотрим представление объемного резонатора в виде колебательного 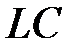контура, а затем установим связь с внешней цепью. Произвольный объемный резонатор в режиме собственных колебаний представим отрезком линии передачи произвольного поперечного сечения с короткозамкнутыми идеальными торцами. Волновое сопротивление линии передачи обозначим 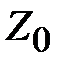, а постоянную распространения 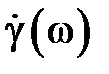. В каждом конкретном случае эти параметры линии известны. Собственные потери резонатора, определяются мнимой частью постоянной распространения 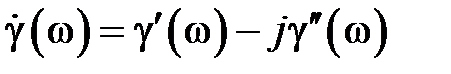, где 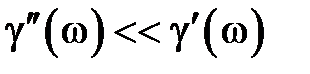. Длина резонатора вблизи резонансной частоты 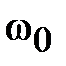близка к половине длине волны в линии 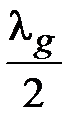либо к кратному значению 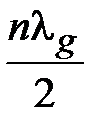. Это значит, что в окрестности резонансной частоты 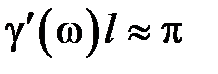, либо 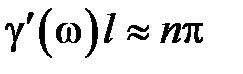. Представление резонатора в виде эквивалентной 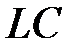цепи вблизи 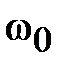основано на трансформации короткого замыкания в торцах линии в произвольную плоскость на длине резонатора. Обычно выбирают одну из двух плоскостей: совпадающую с плоскостью к.з., либо на половине длины резонатора. В первом случае эквивалентное представление объемного резонатора совпадает с последовательным колебательным 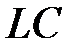контуром, в другом случае с параллельным 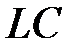контуром. Очевидно, что оба случая эквивалентны и выбор сообразуется исключительно с удобством анализа. Рассмотрим представление объемного резонатора в виде последовательного колебательного контура. Запишем в сечении к.з. торца линии трансформированное сопротивление отрезка линии длиной

.

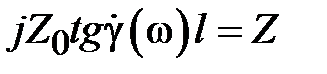Подставим сюда 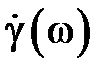и найдем, что

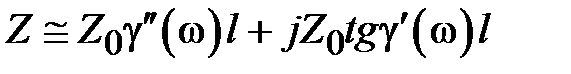. (4.23)

Вблизи резонансной частоты введем малую частотную расстройку 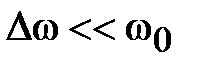. Представим на частоте 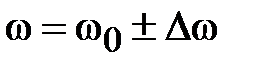вещественную часть постоянной распространения в виде линейной части ряда Тейлора

.

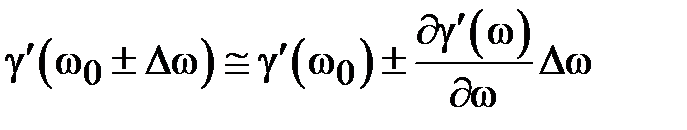Подставим это соотношение в (4.23), учтем, что на резонансной частоте 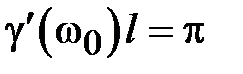, и найдем, что

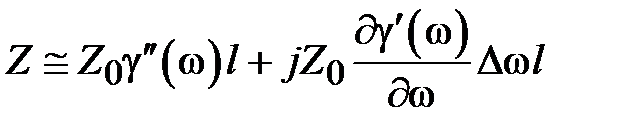. (4.24)

Соотношение (4.24) равно полному сопротивлению последовательного колебательного 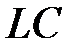контура вблизи резонансной частоты

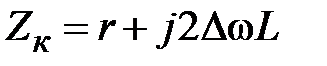. (4.25)

Соотнесем (4.24) и (4.25) друг другу и найдем, что эквивалентное сопротивление омических потерь объемного резонатора равно 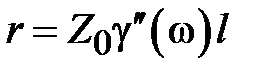, а эквивалентная индуктивность резонатора равна 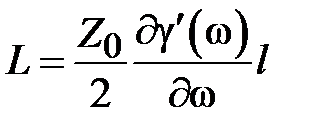. Найдем собственную добротность объемного резонатора как добротность LC контура

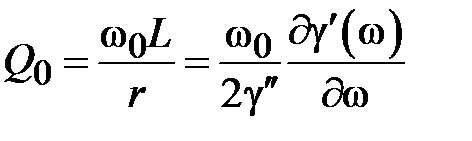. (4.26)

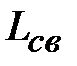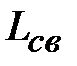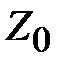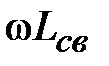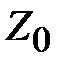Рассмотрим вынужденный режим резонатора. Допустим, что прямоугольный резонатор связан с волноводом одним элементом связи - индуктивной диафрагмой. Эквивалентная схема резонатора с индуктивной связью представлена на рис. 4.4. Слабая связь отвечает малому значению . Со стороны волновода контур нагружен на волновое сопротивление рис. 4.4. Заменим параллельное соединение и эквивалентным последовательным 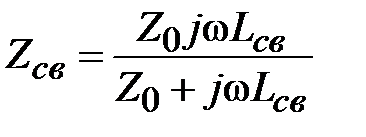. При слабой связ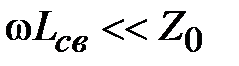и и 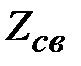преобразуется к виду

.

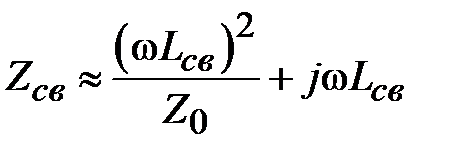Колебательный контур с внесенными в него индуктивностью связи и активным сопротивлением изображен на рис. 4.5. Внесенная индуктивность незначительно изменит резонансную частоту резонатора

,

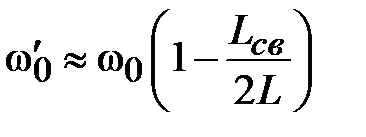а внесенное активное сопротивление связи 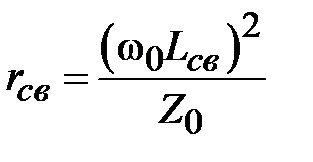определит внешнюю добротность. На основании определения добротности колебательного контура найдем внешнюю добротность как

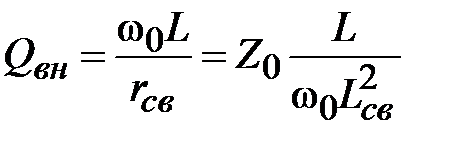. (4.27)

Численную оценку 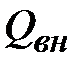получим на основании известной формулы для нормированной эквивалентной проводимости индуктивной диафрагмы

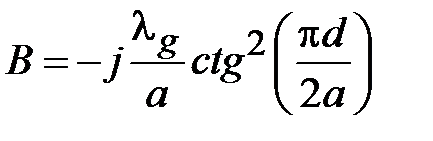, (4.28)

где а – ширина широкой стенки волновода, d – ширина диафрагмы

Представим 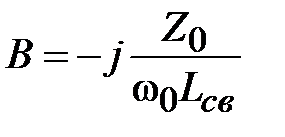и с учетом (4.28) получим, что

.

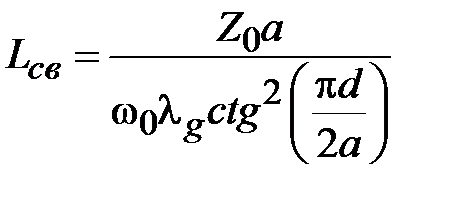ОГЛАВЛЕНИЕ

1. 1. ЛИНИИ ПЕРЕДАЧИ СВЕРХ- ВЫСОКИХ ЧАСТОТ

1.1. Прямоугольные волноводы

1.2. Круглые волноводы

1.3. Прямоугольные волноводы сложного поперечного сечения

1.4. Коаксиальные линии

1.5. Двухпроводные линии передачи

1.6. Несимметричная полосковая линии

1.7. Щелевая линии

1.8. Копланарная линии

1.9. Волны напряжения и тока в прямоугольных волноводах

2. НЕОДНОРОДНОСТИ В ЛИНИЯХ ПЕРЕДАЧИ. СОГЛАСОВАНИЕ ЛИНИЙ ПЕРЕДАЧИ

2.1. Описание электромагнитного процесса в линиях передачи с неоднородностями

2.2. Входное сопротивление отрезка линии передачи

2.3. Трансформирующие свойства отрезка линии передачи

2.4. Широкополосное согласование линий передачи

2.5. Круговая диаграмма сопротивлений

3. ВОЛНОВОДНЫЕ СИММЕТРИЧНЫЕ УСТРОЙСТВА

3.1. Нормированные волны напряжения и тока. Матрица рассеяния

3.2. Свойства матрицы рассеяния

3.3. Матрица рассеяния Т – образного тройника в Е плоскости

3.4. Матрицы рассеяния Т и Y – образных тройников в H плоскости

3.5. Двойное Т сочленение

3.6. Волноводные направленные ответвители

4. ОБЪЕМНЫЕ РЕЗОНАТОРЫ

4.1. Электромагнитные поля в объемных резонаторах

4.2. Собственная добротность объемных резонаторов

4.3. Численная оценка собственной добротности резонаторов

4.4. Объемные резонаторы прямоугольной формы

4.5. Цилиндрические круглые резонаторы

4.6. Квазистационарные объемные резонаторы

4.7. Объемные резонаторы в вынужденном режиме