Занятие 0 2.0 5 .2022г.

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

ПЛАН ЗАНЯТИЯ

Дисциплина: ОДП.01 Математика.

Тема: Сфера и шар . Взаимное расположение сферы и плоскости.

Цель занятия:

Дидактическая :

- ввести основные понятия, связанные с сферой и шаром;

- изучить виды взаимного расположения шара и плоскости;

- формировать навыки решения задач по данной теме.

Воспитательная:

- развивать коммуникативные способности;

- развивать аналитические способности;

- воспитывать самостоятельность, дисциплинированность.

Вид занятия: лекция.

Тип занятия: изучение нового материала.

Форма проведения занятия: репродуктивная и эвристическая беседа.

ПЛАН

1. Актуализация знаний.

2. Понятие сферы, шара и их основные элементы.

3. Уравнение сферы.

4. Взаимное расположение сферы и плоскости.

5. Основные формулы сферы.

6. Примеры и разбор решения задач по данной теме.

Литература:

1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 – 11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровни / Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. – 3-е изд. – М.: Просвещение, 2016. – 463 с.

2. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10 – 11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровни/ Л.С. Атанасян, В.Ф. Бутузов, С.Д. Кадомцев и др. – 3-е изд. – М.: Просвещение, 2016. – 255 с.

1. Актуализация знаний

Повторение раннее изученного материала (определения законспектировать в рабочую тетрадь):

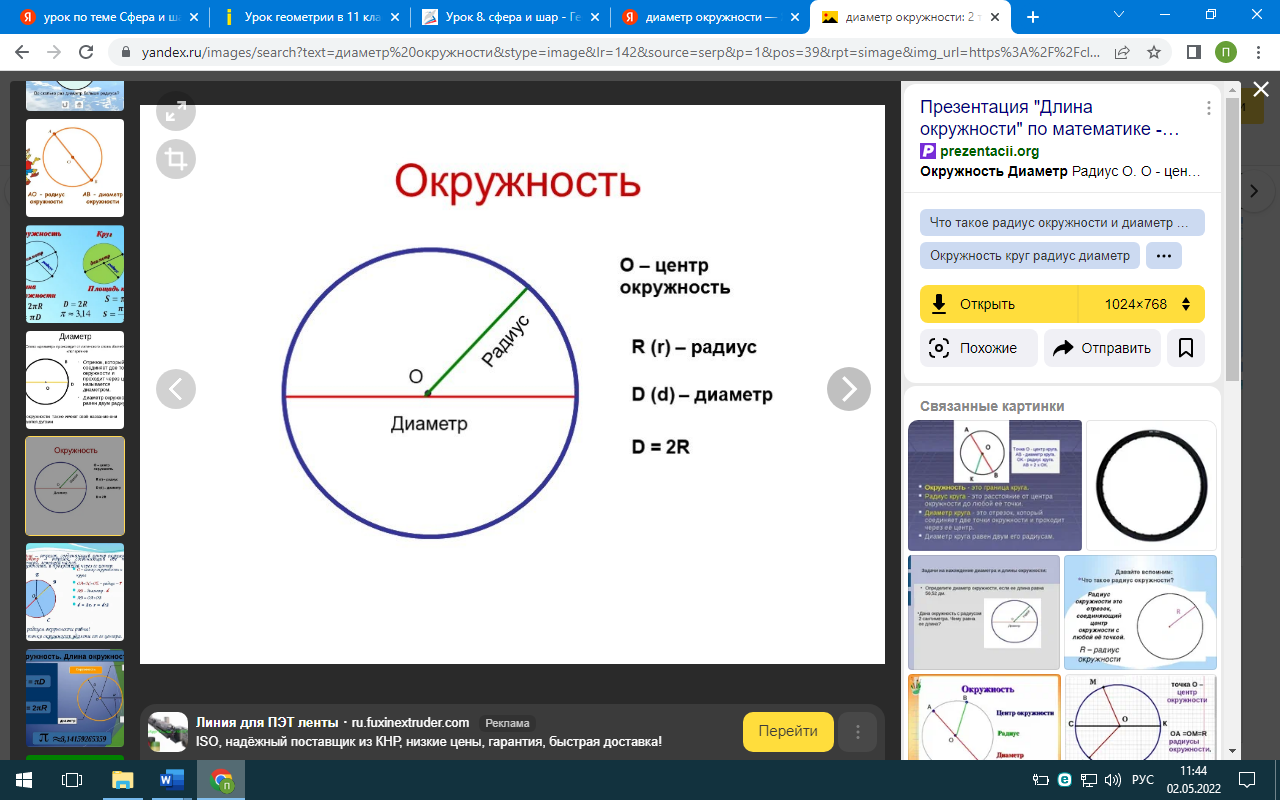
а) Определение окружности. Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности.

б) Определение радиуса окружности. Расстояние от центра до любой точки окружности называется радиусом окружности.

в) Определение диаметра окружности. Отрезок, соединяющий любые две точки окружности и проходящий через её центр называется диаметром окружности. Диаметр равен двум радиусам.

г) Определение круга. Круг – это часть плоскости, ограниченная окружностью.

2. Понятие сферы, шара и их основные элементы.

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

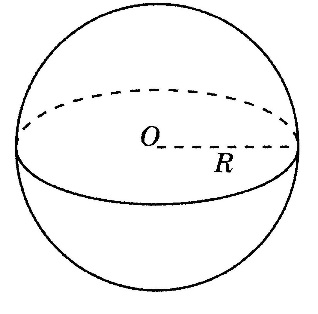
Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Определение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Определение. Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Сферу можно получить ещё одним способом - вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

3. Уравнение сферы

Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=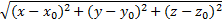

Если точка М лежит на данной сфере, то МС=R, или МС²=R², то есть координаты точки М удовлетворяют уравнению:

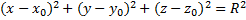Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

4. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть d 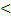R. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть d 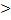R. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Определение. Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости). Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости): Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

5. Основные формулы сферы.

Соотношение между радиусом сферы (R), радиусом сечения (r) и расстоянием от центра сферы до плоскости сечения (h):

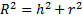
Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR² – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

6. Примеры и разбор решения задач по данной теме

Задача 1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Решение:

Площадь круга вычисляется по формуле: S_кр=πR².

Площадь поверхности шара вычисляется по формуле: S_сф=4πR². Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

Ответ: S_шара =36 кв.ед.

Задача 2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Решение:

Площадь сферы равна S_сф=4πR². То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r² =100, то есть r=10.

Ответ: 10.

Задача 3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Решение:

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

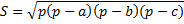, где p – это полупериметр треугольника

p=0,5(AB+BC+AC)=21

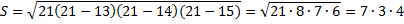
S=84.

С другой стороны, S=p·r,

84=21r

Отсюда r=4.

Теперь найдем расстояние от центра шара до секущей плоскости.

Используем соотношение:

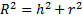
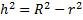
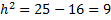
h=3.

Ответ: 3.

Задача 4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Решение:

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

По условию задачи R=10.

Используем соотношение:

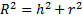
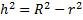
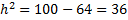
h=6.

Ответ: 6.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Понятие сферы, шара и их основные элементы.

2. Уравнение сферы.

3. Взаимное расположение сферы и плоскости.

4. Основные формулы сферы.

ДОМАШНЕЕ ЗАДАНИЕ

1. Изучить конспект лекции.

2. Ответить на контрольные вопросы в рабочей тетради.

3. Законспектировать разбор решения задач по изученной теме.

4. Фотографию выполненной работы отошлит е в группу .