Если показателем степени является дробь с четным знаменателем , то степень с отрицательным основанием не определяется.
10. 10. 2022 г. 10 класс. Алгебра.
План-конспект урока на тему:
«Степень с рациональным показателем»
(10 класс)
Цели урока:
1. Образовательная - актуализировать субъектный опыт учащихся (опорные знания и способы действий, комплекс знаний), необходимый для изучения нового материала; организовывать деятельность учащихся по восприятию, осмыслению и первичному закреплению знаний и способов действий.
2. Развивающая - развивать умения применять знания на практике, способствовать развитию логического мышления, воли и самостоятельности, развитие умений учебного труда (умение работать в темпе).
3. Воспитательная - создавать условия для воспитания интереса к изучаемой теме, воспитания мотивов учения, положительного отношения к знаниям, воспитания дисциплинированности, обеспечивать условия успешной работы в коллективе.
Тип урока: Урок изучения и первичного закрепления знаний и способов действий.
Объяснение учебного материала.
Понятие степени 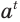
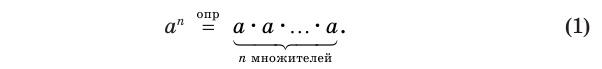
Здесь символом 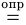 подчеркивается, что равенство (1) особое: это равенство-определение, и поэтому не требует обоснования в отличие, например, от равенства
подчеркивается, что равенство (1) особое: это равенство-определение, и поэтому не требует обоснования в отличие, например, от равенства 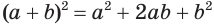 .
.
Определение-равенство (1) осмысленное только для тех натуральных значений показателя 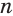 , которые не меньше 2, так как умножение есть двуместное действие. Поэтому натуральная степень
, которые не меньше 2, так как умножение есть двуместное действие. Поэтому натуральная степень 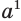 требует особого определения, но такого, при котором сохраняются свойства натуральной степени, в частности, свойство
требует особого определения, но такого, при котором сохраняются свойства натуральной степени, в частности, свойство 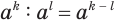 . С учетом этого должно быть:
. С учетом этого должно быть: 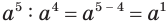 . Вместе с этим
. Вместе с этим 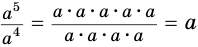 . Поэтому первую степень
. Поэтому первую степень 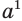 целесообразно определить так:
целесообразно определить так:

Так же, поскольку 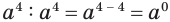 и вместе с этим
и вместе с этим 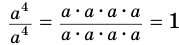 , то нулевую степень
, то нулевую степень 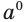 целесообразно определить так:
целесообразно определить так:

Обратив внимание, например, на то, что 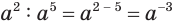 и вместе с этим
и вместе с этим 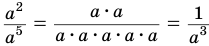 приходим к выводу, что отрицательную целую степень
приходим к выводу, что отрицательную целую степень 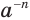 , где
, где 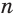 — натуральное число, целесообразно определить так:
— натуральное число, целесообразно определить так:

При этом, если в равенствах (1) и (2) основание 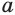 может иметь любое действительное значение, то в равенствах (3) и (4) это значение должно быть отличным от нуля.
может иметь любое действительное значение, то в равенствах (3) и (4) это значение должно быть отличным от нуля.
Рациональную степень 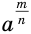 с положительным основанием
с положительным основанием 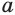 введем из следующих соображений. Для целых показателей
введем из следующих соображений. Для целых показателей 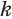 и
и 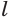 выполняется свойство
выполняется свойство 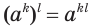 . Желательно, чтобы оно выполнялось и для дробных показателей. В таком случае будет
. Желательно, чтобы оно выполнялось и для дробных показателей. В таком случае будет 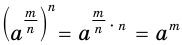 . Но равенство
. Но равенство 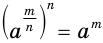 означает, что число
означает, что число 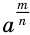 должно быть корнем
должно быть корнем 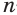 -й степени из числа
-й степени из числа 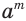 :
:

Примеры:
С учетом определения (5) получим:
а) 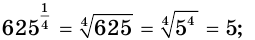
б) 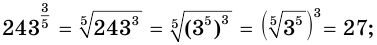
в) 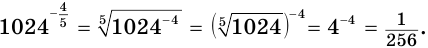
Из определения степени с рациональным показателем следует, что при любом положительном значении основания а и любом рациональном значении показателя 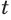 число
число 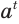 является положительным.
является положительным.
Поскольку, с учетом свойств корня, 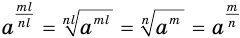 , то значение рациональной степени а' не зависит от того, какой дробью из множества равных дробей представлен рациональный показатель
, то значение рациональной степени а' не зависит от того, какой дробью из множества равных дробей представлен рациональный показатель 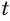 .
.
Если показателем степени является дробь 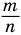 с нечетным знаменателем
с нечетным знаменателем 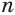 , определение (5) распространяется и на отрицательные значения основания
, определение (5) распространяется и на отрицательные значения основания 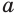 .
.
Пример:
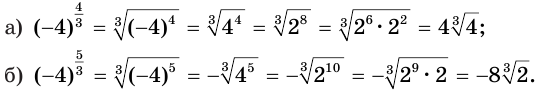
Если показателем степени является дробь 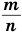 с четным знаменателем
с четным знаменателем 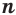 , то степень
, то степень 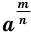 с отрицательным основанием не определяется.
с отрицательным основанием не определяется.
Степень 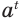 положительного числа
положительного числа 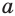 с иррациональным показателем
с иррациональным показателем 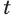 определяется так.
определяется так.
Пусть 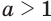 . Для числа
. Для числа 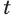 выпишем последовательности
выпишем последовательности
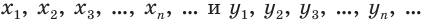
его десятичных приближений по недостатку и по избытку соответственно. Тогда
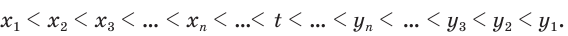
Из этих неравенств с учетом того, что если 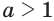 и
и 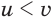 , то
, то 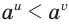 , получим:
, получим:
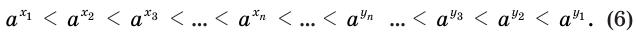
Оценим разность 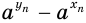 . Получим:
. Получим:
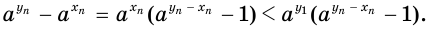
Если значение переменной 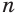 неограниченно увеличивается, то значение выражения
неограниченно увеличивается, то значение выражения  стремится к нулю, значение выражения
стремится к нулю, значение выражения 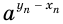 — к единице, а значение выражения
— к единице, а значение выражения 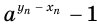 , а потому и выражения
, а потому и выражения 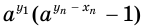 — к нулю. Это означает, что значения выражений
— к нулю. Это означает, что значения выражений 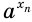 и
и 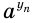 приближаются друг к другу. Можно доказать, что есть только одно число
приближаются друг к другу. Можно доказать, что есть только одно число 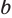 , для которого
, для которого 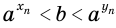 при всех
при всех 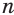 . Оно и принимается в качестве значения иррациональной степени
. Оно и принимается в качестве значения иррациональной степени 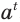 .
.
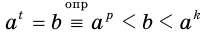 , где
, где 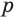 и
и 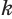 — рациональные приближения иррационального числа
— рациональные приближения иррационального числа 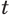 по недостатку и по избытку соответственно.
по недостатку и по избытку соответственно.
Так же определяется иррациональная степень 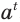 для
для 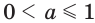 . При этом для любого действительного показателя
. При этом для любого действительного показателя 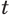

Отметим, что если действительный показатель 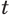 больше нуля, то
больше нуля, то 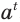 имеет смысл и при
имеет смысл и при 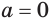 , именно:
, именно:
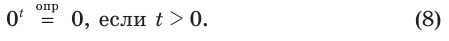
Пример:
Рассмотрим иррациональную степень 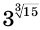 . Учитывая, что
. Учитывая, что
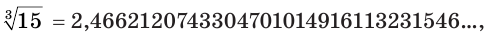
получим:
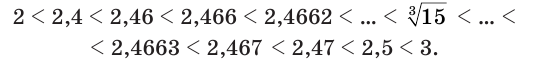
Поэтому

или
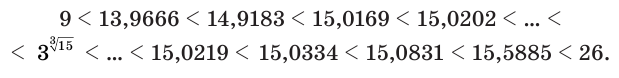
Вычисление на калькуляторе для числа 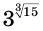 дает:
дает:
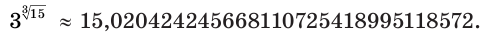
Для степени с действительным показателем верны известные вам основные свойства степени:
-
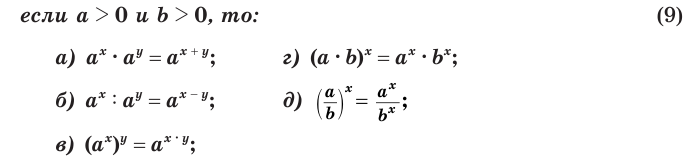
- если
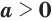 , то выражение
, то выражение 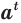 имеет значение при любом значении переменной
имеет значение при любом значении переменной 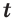 ; (10)
; (10) - если
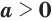 , то
, то 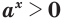 при любом значении переменной
при любом значении переменной 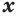 ; (11)
; (11) - если
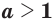 , то
, то 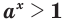 при
при 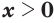 и
и 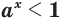 при
при 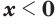 ; (12)
; (12) - если
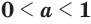 , то
, то 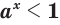 при
при 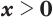 и
и 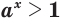 при
при 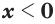 ; (13)
; (13) - если
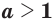 и
и 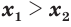 , то
, то 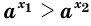 ; (14)
; (14) - если
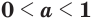 и
и 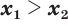 , то
, то 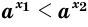 . (15)
. (15)
Докажем, например, что 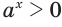 при любом иррациональном значении переменной
при любом иррациональном значении переменной 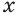 .
.
Если 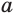 = 1, то
= 1, то 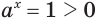 .
.
Пусть 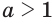 ,
, 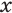 — иррациональное число,
— иррациональное число, 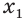 и
и 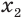 — рациональные приближения к
— рациональные приближения к 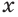 по недостатку и избытку:
по недостатку и избытку: 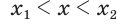 . Из определения иррациональной степени следует, что
. Из определения иррациональной степени следует, что 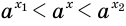 , а поскольку
, а поскольку 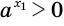 , то и
, то и 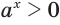 .
.
Если 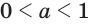 , то так же получим, что
, то так же получим, что 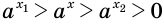 .
.
Понятием степени с натуральным показателем пользовались уже в Древней Греции. Об этом свидетельствуют термины квадрат числа и куб числа, известные с тех времен. Современные обозначения натуральной степени 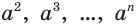 ввел в 1637 г. французский математик Рене Декарт. Французский математик Николя Орем (около 1323—1382) уже пользовался дробными показателями. Отрицательные и нулевой показатели ввел в обиход французский математик Николя Шюке (около 1445 — около 1500). Нидерландский ученый и инженер Симон Стевин (1548—1620) обратил внимание на то, что
ввел в 1637 г. французский математик Рене Декарт. Французский математик Николя Орем (около 1323—1382) уже пользовался дробными показателями. Отрицательные и нулевой показатели ввел в обиход французский математик Николя Шюке (около 1445 — около 1500). Нидерландский ученый и инженер Симон Стевин (1548—1620) обратил внимание на то, что 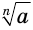 целесообразно понимать как
целесообразно понимать как 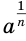 . Знак
. Знак 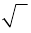 для обозначения корня впервые использовал в 1525 г. чешский математик Криштян Рудольф (около 1500 — около 1545), а современный символ
для обозначения корня впервые использовал в 1525 г. чешский математик Криштян Рудольф (около 1500 — около 1545), а современный символ 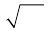 с горизонтальной чертой сверху ввел Декарт.
с горизонтальной чертой сверху ввел Декарт.
№1. Представьте степень с дробным показателем в виде корня:
а) 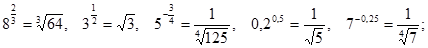
б) 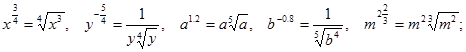
в) 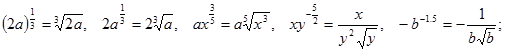
г) 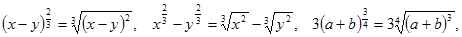
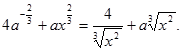
№2. Представьте арифметический корень в виде степени с дробным показателем:
а) 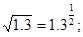
| е) 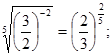
|
б) 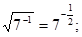
| ж) 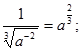
|
в) 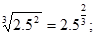
| з) 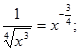
|
г) 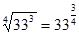
| и) 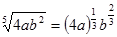
|
д) 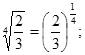
| к) 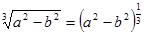
|
№3. Вычислите:
а) 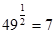 ; ;
| в) 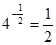 ; ;
| д) 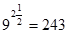 ; ;
| ж) 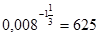 ; ;
|
б) 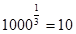 ; ;
| г) 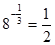 ; ;
| е) 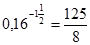 ; ;
| з) 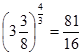 . .
|
№4. Сравните:
а) 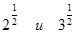 ; ;
| в) 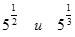 ; ;
|
б) 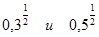 ; ;
| г) 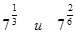 . .
|
Ответы: а) меньше, б) меньше, в) больше, г) равно.
5.Замените арифметический корень степенью с дробным показателем.
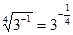 ; ;
| 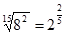 ; ;
| 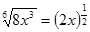 ; ;
| 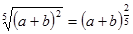 ; ;
|
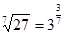 ; ;
| 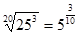 ; ;
| 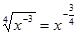 ; ;
| 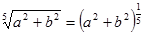 . .
|
6.6Вычислите:
а) 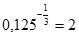 ; ;
| б) 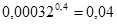 ; ;
| в) 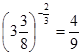 ; ;
| г) 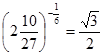 . .
|
6.Найти область определения функции:
а) 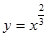 ; ;
| б) 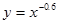 ; ;
| в) 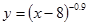 ; ;
| г) 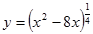 . .
|
Ответы: а) x≥0, б) x>0, в) x>8, г) xÎ(-¥, 0] È [8, +¥).








