5 .Проверка на устойчивость исходной САУ по критерию Гурвица .

Кафедра "Электронные, радиоэлектронные и электротехнические системы"
Дисциплина "Теория Автоматического Управления"
Курсовая работа
СИНТЕЗ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ЗАДАННЫМ КАЧЕСТВОМ
Вариант №5
БГТУ 210100.011 000 ПЗ
Студент группы 12-ЭиН1:
Колосовский И. В.
Проверил преподаватель:
Малаханов А. А.
Брянск, 2014
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 2 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
| Разраб. |
| КолосовскийИ.В. |
| Провер. |
| Малаханов А. А. |
| Реценз. |
| Н. Контр. |
| Утверд. |
| Лит. |
| Листов |
| 24 |
| Гр.12-ЭиН1 |
Содержание
Введение...................................................................................................................3
1. Расчет коэффициента усиления регулятора (K) при изменении задания (g) и возмущения (z) в указанных диапазонах...........................................................4
2. Расчет и построение внешних статических характеристик замкнутой САУ...........................................................................................................................6
3. Определение передаточной функции исходной САУ, расчет корней характеристического уравнения............................................................................7
4. Расчет и построение частотных характеристик эквивалентной разомкнутой САУ: АФЧХ, ЛАЧХ и ЛФЧХ.................................................................................8
5. Проверка на устойчивость исходной САУ по критерию Гурвица…...............................................................................................................13
6. Моделирование переходных характеристик исходной САУ: а) при отсутствии возмущений для граничных значений g; б) при воздействии максимального возмущения в установившемся режиме по заданию для граничных значений g. Определение типовых показателей качества САУ в динамике.................................................................................................................13
7. Синтез корректирующего устройства, обеспечивающего настройку исходной системы на технический оптимум при...............................................16
8. Моделирование переходных характеристик САУ, скорректированной на технический оптимум...........................................................................................18
Заключение.............................................................................................................20
Список используемой литературы.......................................................................21
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 3 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
Введение.
Курсовая работа по дисциплине «Теория автоматического управления» предполагает изучение составляющих дисциплины и приобретение навыков расчета параметров элементов систем автоматического управления (САУ) и анализа их характеристик. Данная работа предусматривает возможность практического применения знаний, полученных на лекциях, лабораторных работах и в процессе самостоятельной подготовки. При выполнении курсовой работы необходимо решить ряд задач, тематика которых отражает основные разделы изучаемой дисциплины.
Параметры исходной САУ
a1 = 0 b2= 0,021 c1= 0 ,11 d2= 0 g= 1.1 ... 9
a0= 8 b1= 0.322 c0 = 5 d1= 0.07 z= -7
Статистическая ошибка 2,4 %
1. Расчет коэффициента усиления регулятора ( K ) при изменении задания ( g ) и возмущения ( z ) в указанных диапазонах.
Рассчитаем коэффициент усиления САУ, обеспечивающий заданную максимально допустимую суммарную статическую ошибку в заданном диапазоне изменения входных воздействий.
Кроме коэффициента усиления на величину ошибки  ε влияют значения управляющего и возмущающего воздействий. Наибольшая величина ε достигается при действии на систему минимального управляющего воздействия g и максимального возмущения z. Т. е. при единичном коэффициенте передачи цепи обратной связи исходной системы суммарная статическая ошибка может быть найдена как:
ε влияют значения управляющего и возмущающего воздействий. Наибольшая величина ε достигается при действии на систему минимального управляющего воздействия g и максимального возмущения z. Т. е. при единичном коэффициенте передачи цепи обратной связи исходной системы суммарная статическая ошибка может быть найдена как:
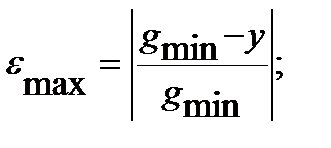 где y- выходная переменная.
где y- выходная переменная.
Значение y определяется реакцией САУ на сумму управляющего и возмущающего воздействий:
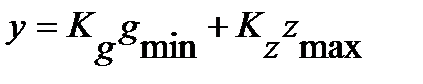 где
где 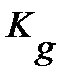 ,
, 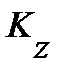 - суммарные коэффициенты усиления задающего и возмущающего воздействий. Найдем
- суммарные коэффициенты усиления задающего и возмущающего воздействий. Найдем 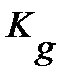 . Для этого примем z=0
. Для этого примем z=0
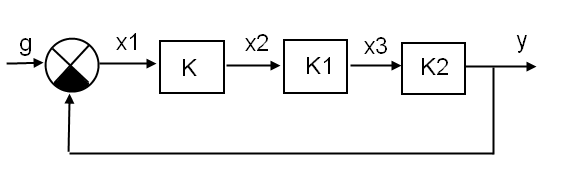
Рис.1 Графическое изображение исходной САУ при отсутствии
возмущений z.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 4 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
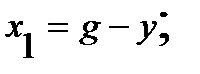
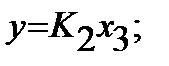
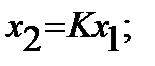
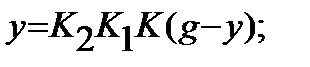
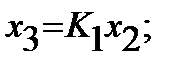
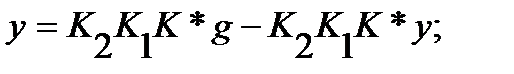
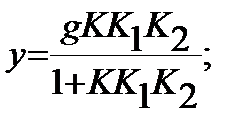
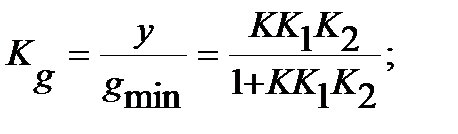
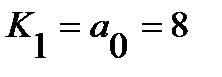 и
и 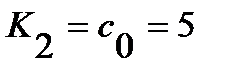 =>
=> 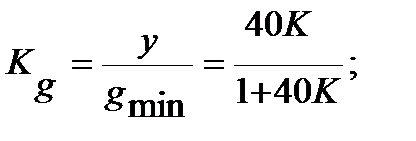
Найдем 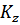 , примем g=0
, примем g=0
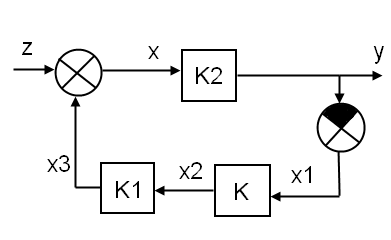
Рис. 2. Графическое изображение исходной САУ при отсутствии заданий g
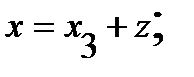
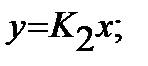
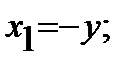
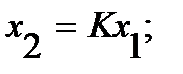
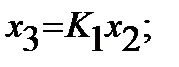
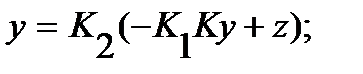
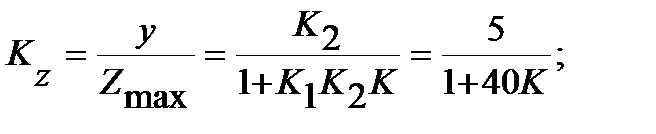
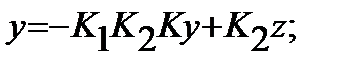
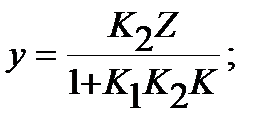
Итак: 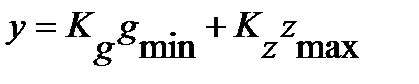 и
и 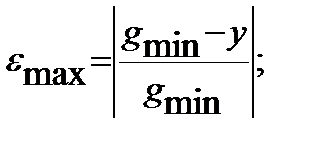 тогда
тогда 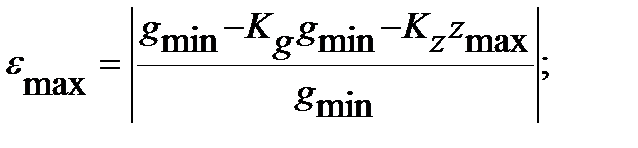
По условию 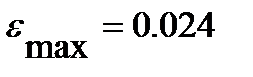 найдем коэффициент К
найдем коэффициент К
Значение выходной переменной, соответствующее наибольшему отклонению при 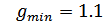 и
и 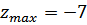 :
:
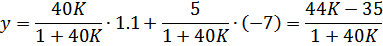
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 5 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
Статическая ошибка:
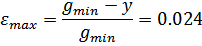
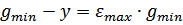
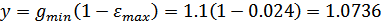
Коэффициент передачи САУ, обеспечивающий заданную максимальную статическую ошибку:
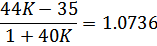
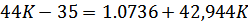
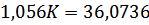
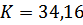
Таким образом, для обеспечения максимальной статической ошибки 2.4% при заданных диапазонах изменения задающего воздействия g и возмущающего воздействия z, коэффициент передачи САУ должен быть не менее 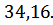
2. Расчет и построение внешних статических характеристик замкнутой САУ.
Построим семейства внешних статических характеристик для замкнутой САУ в заданном диапазоне g и z. Аналитически характеристики заданы уравнением. Запишем уравнение для данной САУ на основе ее структурной схемы:
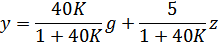
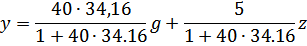
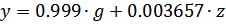
При gmin =1.1 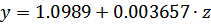
| z | 0 | -7 |
| y | 1.0989 | 1.073301 |
При g =5 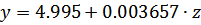
y= 5(1-0.024)= 4.88
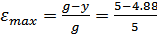 × 100% = 2.4%
× 100% = 2.4%
| z | 0 | -7 |
| y | 4.995 | 4.9694 |
При g =9 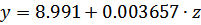
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 6 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
y= 9(1-0.024)= 8.784
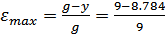 × 100% = 2.4%
× 100% = 2.4%
| z | 0 | -7 |
| y | 8.991 | 8.9654 |
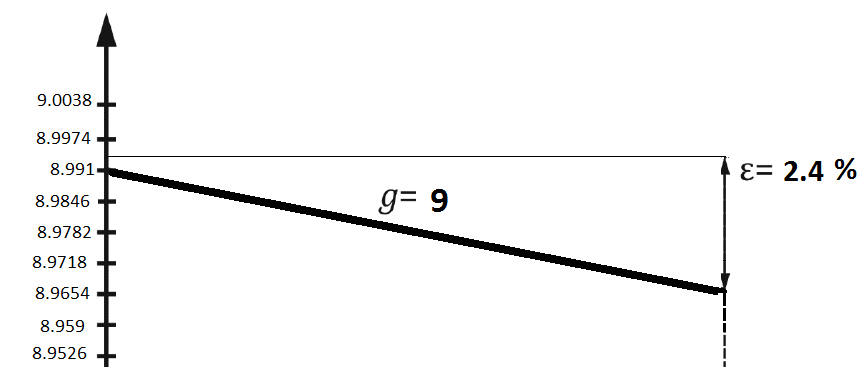
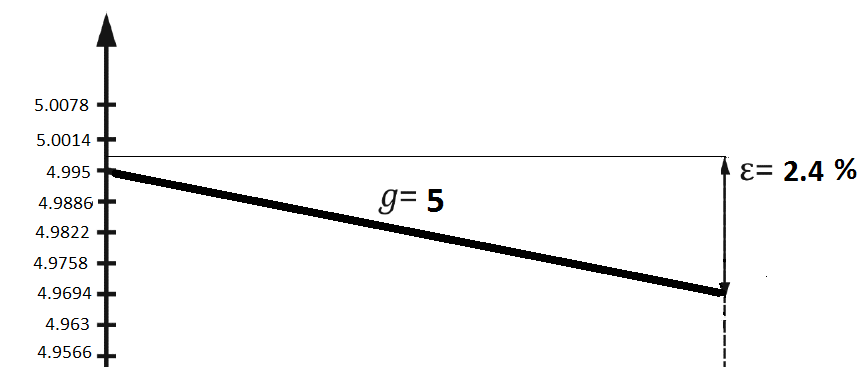
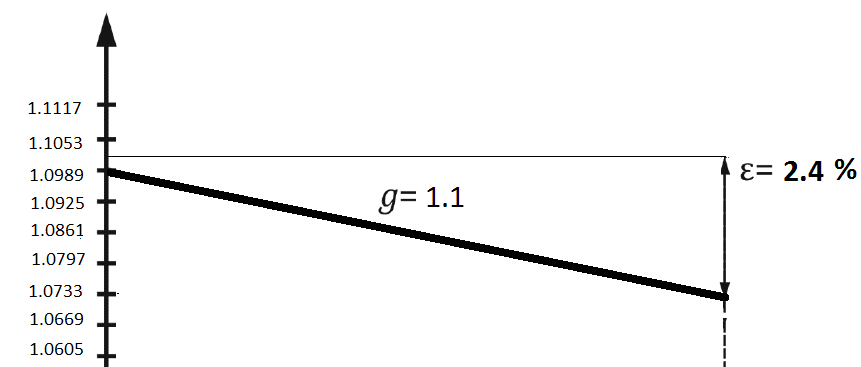
Рис .3 График семейства статических характеристик.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 7 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
3. Определение передаточной функции исходной САУ, расчет корней характеристического уравнения
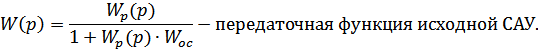
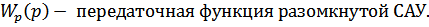
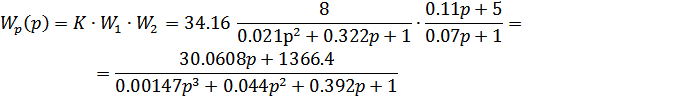
Так как обратная связь единична, то 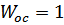 , значит
, значит
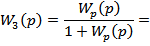

Знаменатель передаточной функции - это характеристический полином системы:
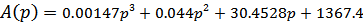
Корни этого полинома определяют вид и параметры переходной характеристики САУ. Решая кубическое уравнение в среде MathCAD,получаем корни:
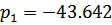
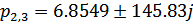
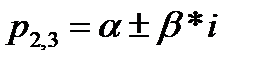
Так как вещественные части корней характеристического уравнения отрицателен и положительны, то можно сделать вывод о том, что система может быть как устойчива, так и неустойчива.
Кроме того, наличие корня с отрицательной вещественной частью и корней с положительной вещественной частью свидетельствует о расходящихся колебаниях с частотой 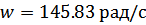 , периодом
, периодом 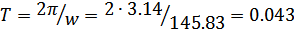 ,
,
Декремент колебаний:
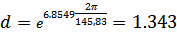
Коэффициент расхождения: 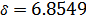
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 8 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
4. Расчет и построение частотных характеристик эквивалентной разомкнутой САУ: АФЧХ, ЛАЧХ и ЛФЧХ.
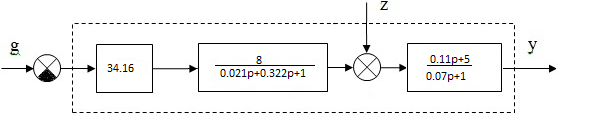
Рис.4. Структурная схема разомкнутой САУ
Разомкнутая САУ – система, не способная контролировать состояние объекта управления, т.е. это САУ без обратной связи. Передаточная функция разомкнутой САУ выглядит следующим образом:
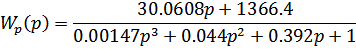
Комплексно-частотная функция имеет вид:
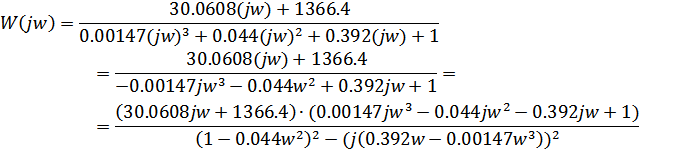
Числитель:
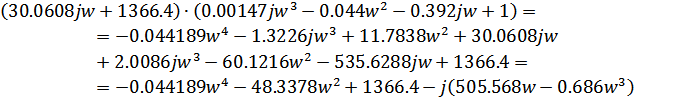
Знаменатель:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 9 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
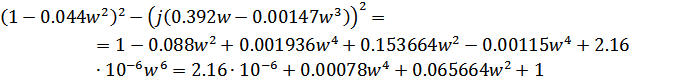
Получаем:
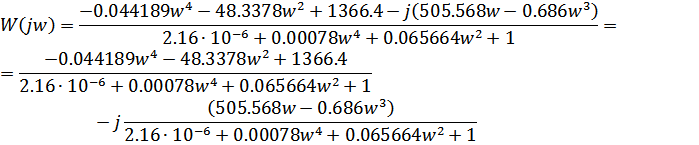
Логарифмические частотные характеристики определяют усилительные свойства системы (ЛАЧХ) и сдвиг фазы выходной величины (ЛФЧХ).
ЛАЧХ – модуль комплексной функции АФЧХ с учетом логарифмического масштаба, а ЛФЧХ – аргумент комплексной функции.
Уравнение ЛАЧХ:
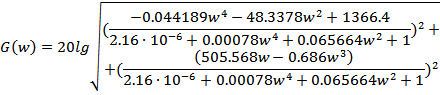
Уравнение ЛФЧХ:
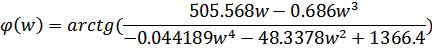
Построим с помощью пакета MatLab логарифмические амплитудную частотную характеристику (ЛАЧХ), фазово-частотную характеристику (ЛФЧХ) и амплитудную фазово-частотную характеристику (АФЧХ) для разомкнутой системы. Структурная схема разомкнутой САУ в среде MatLabпредставлена на рис.4.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 10 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
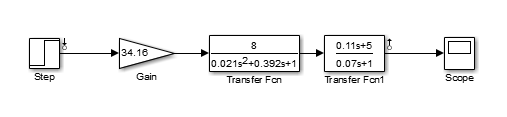
Рис.5. Схема разомкнутой САУ в MatLab
Результаты построений представлены на рис.5, рис.6 и рис.7.
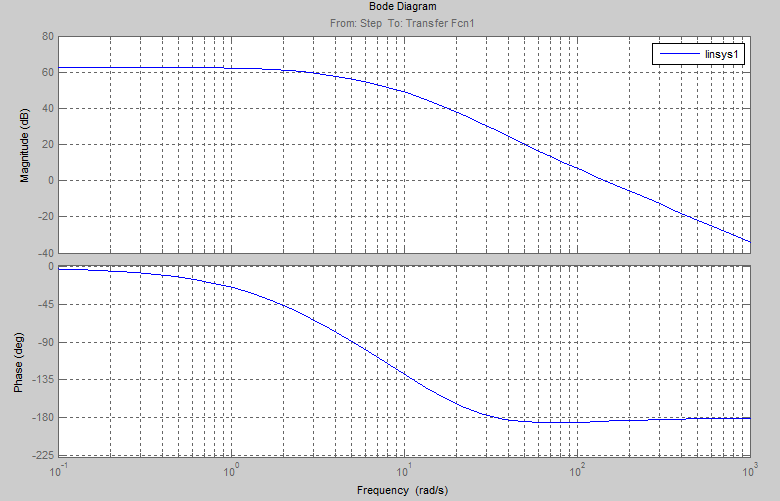
Рис.6. Графики ЛАЧХ и ЛФЧХ разомкнутой САУ
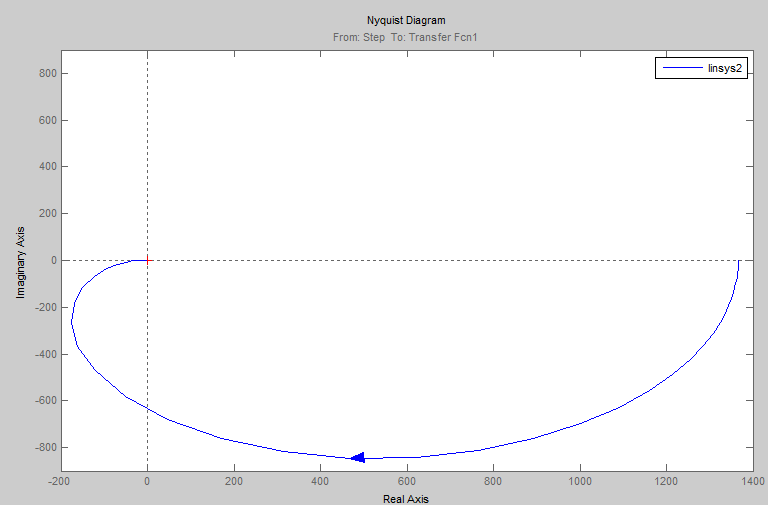
Рис.7. График АФЧХ разомкнутой САУ
Для проверки построим все графики в MathCad:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 11 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
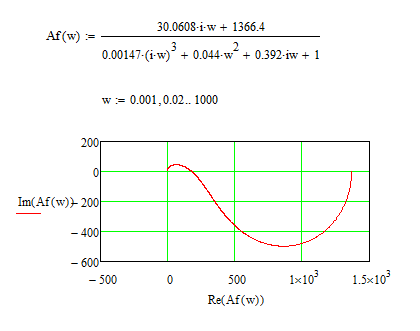
Рис. 7. АФЧХ, построенная в MathCad
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 12 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
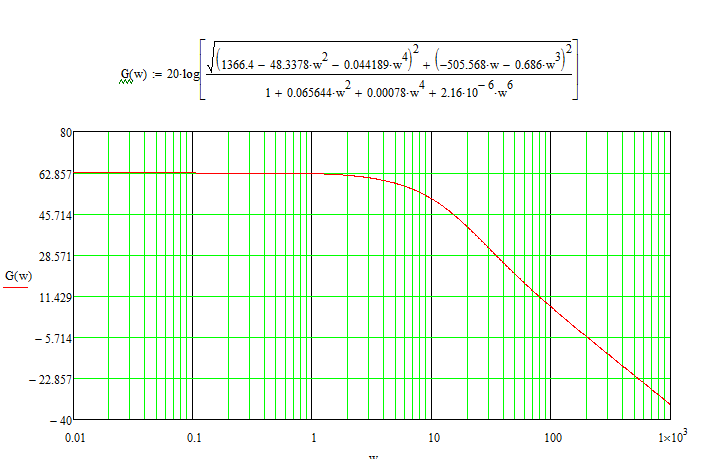
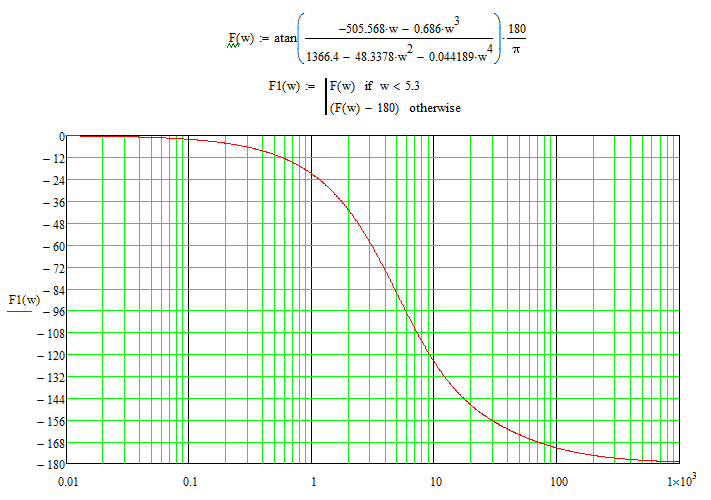
Рис. 8. ЛАЧХ и ЛФЧХ, построенные в MathCad
5 .Проверка на устойчивость исходной САУ по критерию Гурвица .
Из пункта 3 получили характеристический полином:
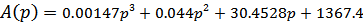
Для того, что бы составить определитель Гурвица надо по диагонали от левого верхнего до правого нижнего выписать все коэффициенты. Пустые строки заполняем так, что бы чередовались строки с нечетными и четными индексами и когда коэффициент отсутствует на месте его пишем0. Строим определитель Гурвица: p2

| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 13 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
По определению САУ устойчива, если определитель Гурвица и все его диагональные миноры положительны:
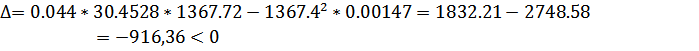
Отсюда следует, что САУ является неустойчивой.
6.Моделирование переходных характеристик исходной САУ: а) при отсутствии возмущений для граничных значений g ; б) при воздействии максимального возмущения в установившемся режиме по заданию для граничных значений g . Определение типовых показателей качества САУ в динамике.
1.) При отсутствии возмущений для граничных значений g. Структурная схема для моделирования в MatLab представлена на рис.8.
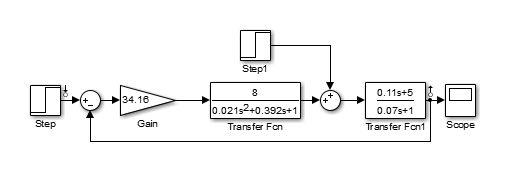
Рис.8. Схема исходной САУ в MatLab
1.1.) Здесь g не изменяется и равно своему минимальному значению 1.1, возмущающее воздействие z тоже равно своему минимальному значению 0. Результат моделирования представлен на рис.9.
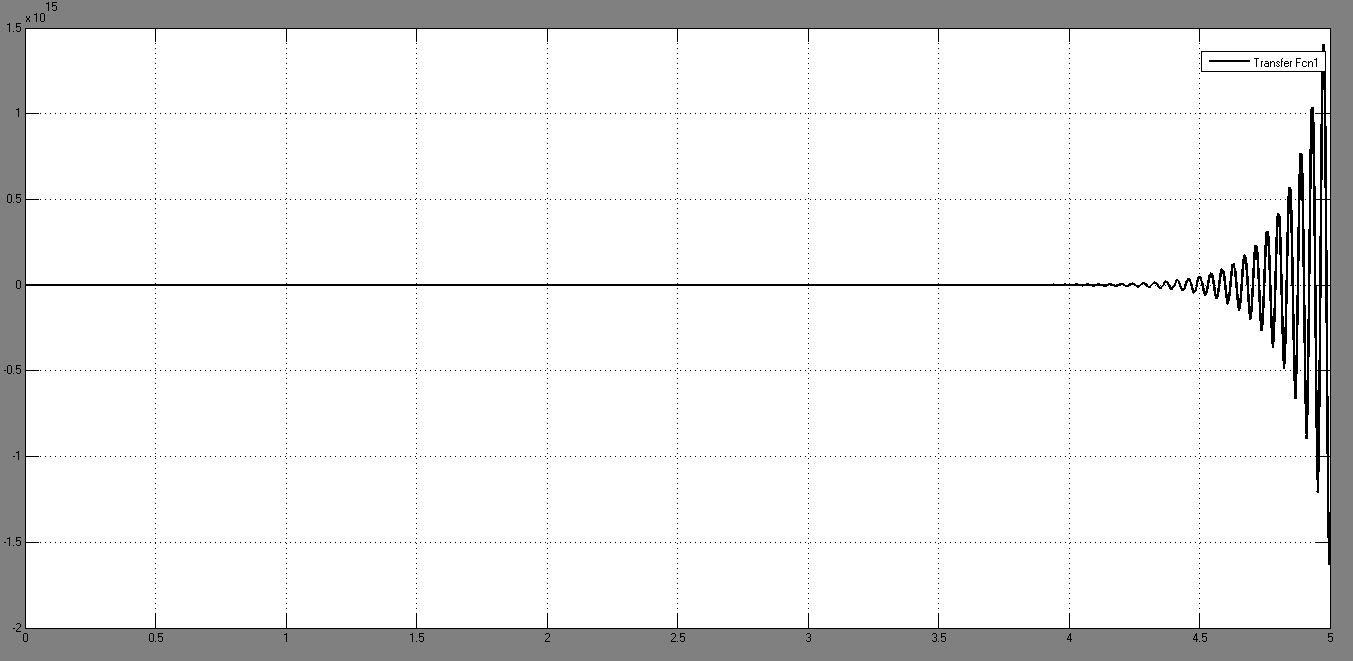
Рис.9 Переходная характеристика САУ при отсутствии возмущений (gmin=1,1)
САУ не устойчива, колебания происходят с нарастающей амплитудой.
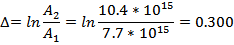
Период колебаний:
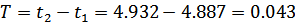
Частота колебаний:
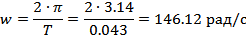
Коэффициент расхождения:
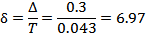
Декремент расхождения:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 14 |
| БГТУ. 2 10104 . 09. 000. ПЗ |
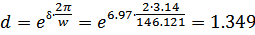
Как видим, частота ( 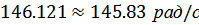 ) и декремент затухания (
) и декремент затухания ( 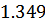
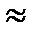
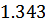 ) имеют погрешность менее 1% с ранее рассчитанными по п. 3, тем самым мы доказали правильность выполнения расчетов.
) имеют погрешность менее 1% с ранее рассчитанными по п. 3, тем самым мы доказали правильность выполнения расчетов.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 13 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
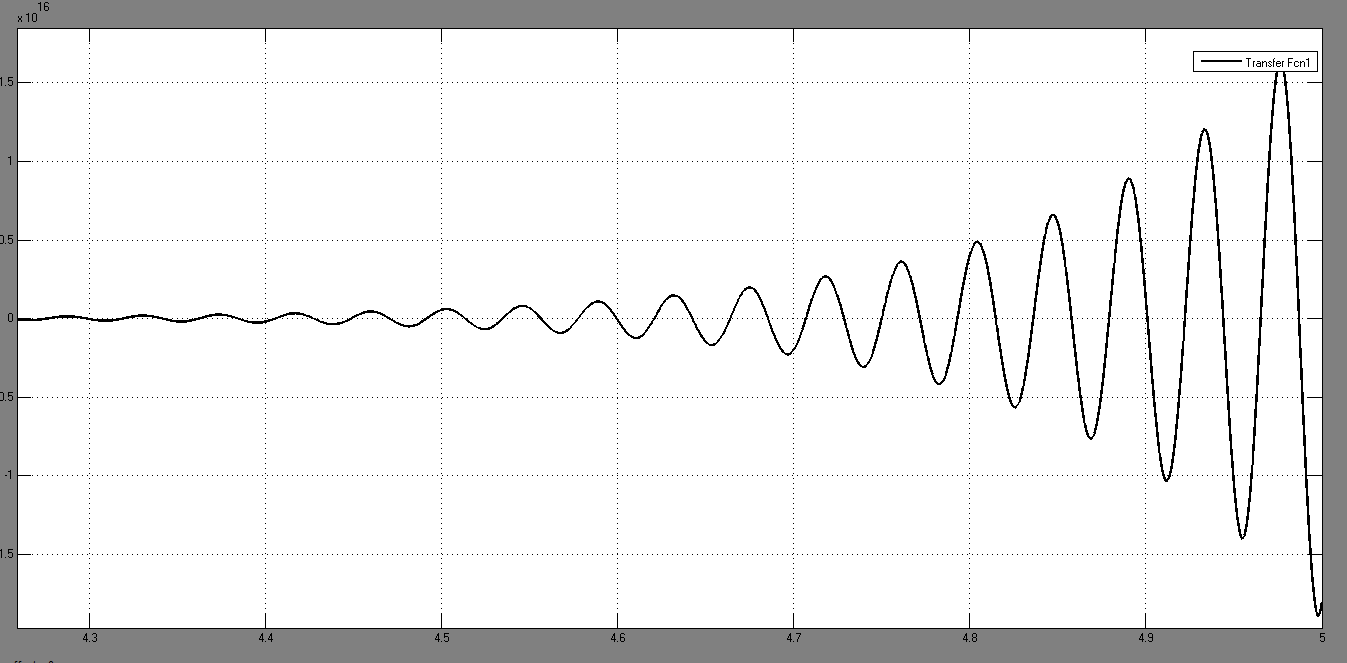
1.2.) Здесь g не изменяется и равно своему максимальному значению 9, возмущающее воздействие z равно своему минимальному значению 0. Результаты моделирования представлены на рис.10.
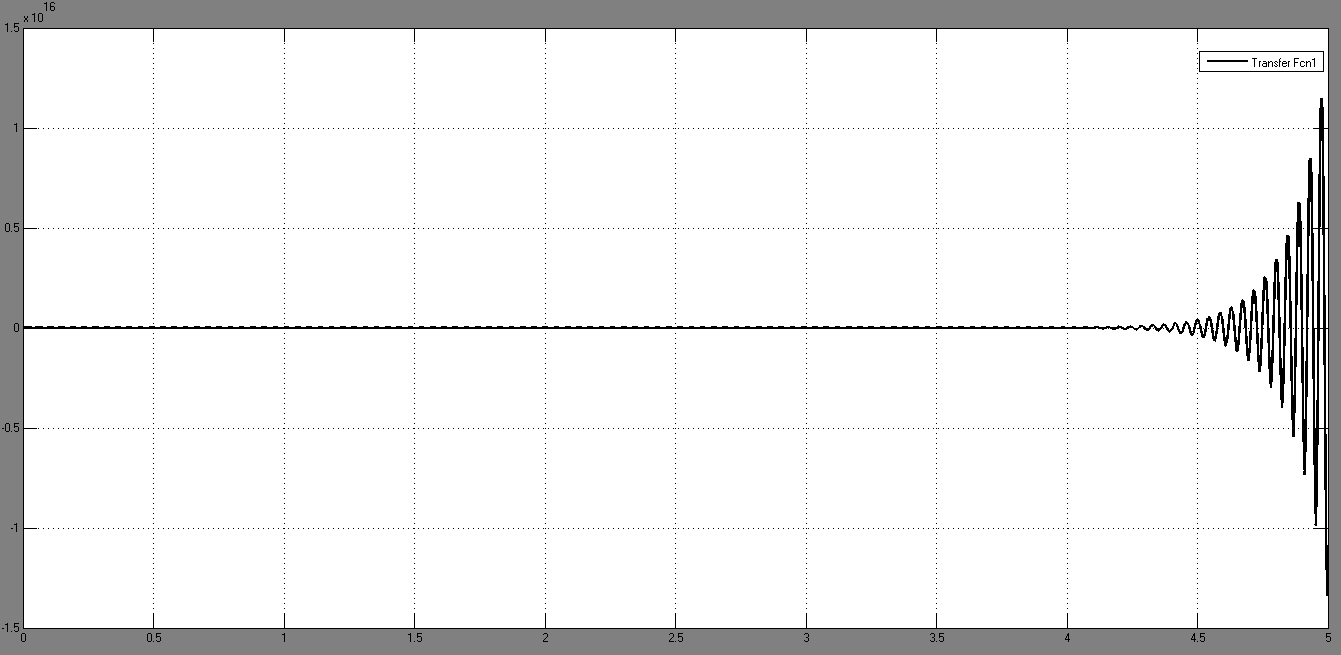
Рис.10. Результат моделирования при 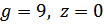
САУ не устойчива, колебания происходят с нарастающей амплитудой. Амплитуда нарастает быстрее, чем в предыдущем случае.
Как видим, частота 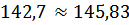 рад/c, коэффициент расхождения
рад/c, коэффициент расхождения 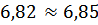 логарифмический декремент расхождения
логарифмический декремент расхождения 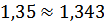
2.)При действующих максимальных и минимальных возмущениях z для граничных значений g.
2.1.)Здесь g равно минимальному значению 1.1, возмущающее воздействие z сначала равно своему минимальному значению 0...-7Результаты моделирования представлены на рис.11.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 15 |
| БГТУ. 2 10104 . 09. 000. ПЗ |
Рис.11. Результат моделирования при 
2.2.)Здесь gравно максимальному значению 14, возмущающее воздействие zсначала равно своему минимальному значению 0...-5. Результаты моделирования представлены на рис.12.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 16 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
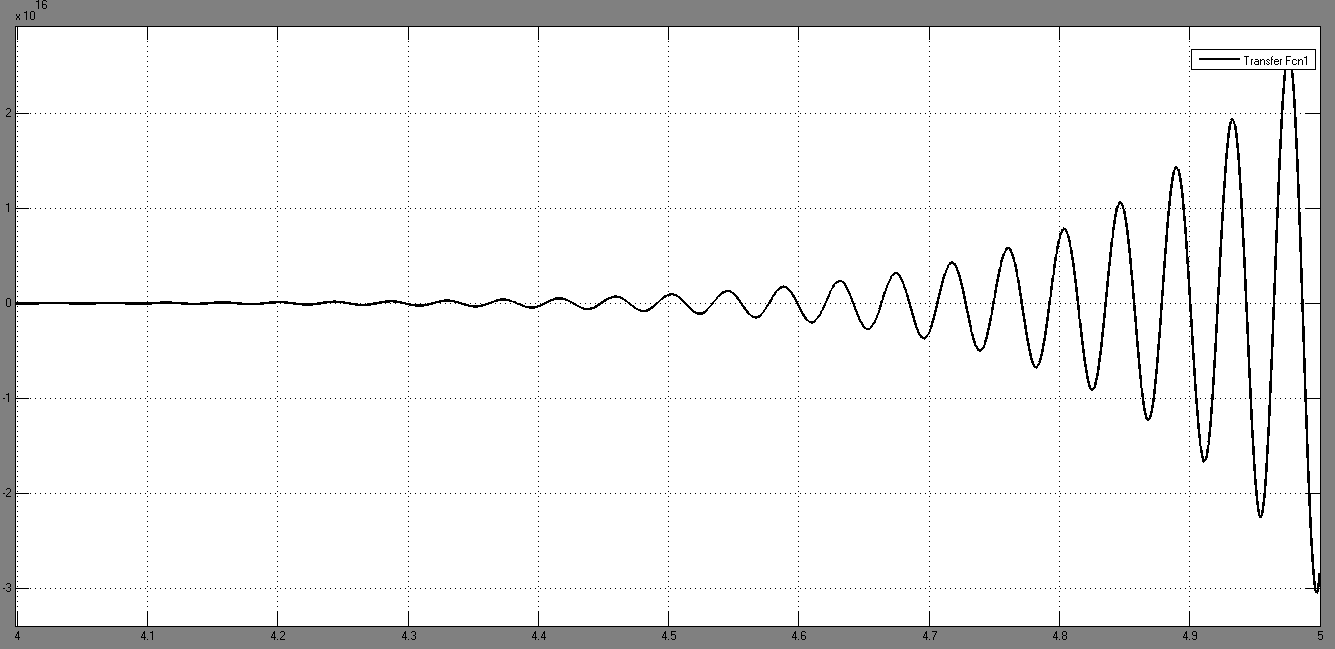
Рис.12. Результат моделирования при 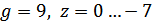
7. Синтез корректирующего устройства, обеспечивающего настройку исходной системы на технический оптимум при.  Рис.13. Структурная схема скорректированной САУ
Рис.13. Структурная схема скорректированной САУ
Желаемая передаточная функция разомкнутой системы, настроенной на технический оптимум, имеет вид:
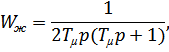
где 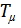 - наименьшая постоянная времени нескорректированной системы
- наименьшая постоянная времени нескорректированной системы
Передаточная функция разомкнутой САУ имеет вид:
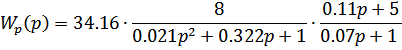
Определим коэффициент демпфирования первой передаточной функции:
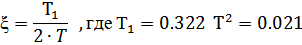
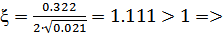
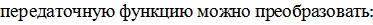
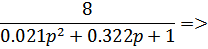
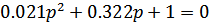 корни этого уравнения p1 = -4.326 и p2 = -11.007
корни этого уравнения p1 = -4.326 и p2 = -11.007
1/p1 = -0.231 1/p2 = -0.091
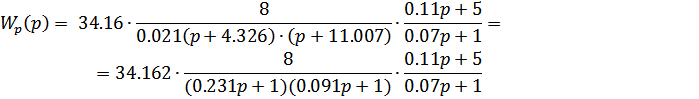
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 17 |
| БГТУ. 2 10100 . 11 . 000. ПЗ |
За 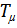 принимаем минимальное из постоянных времени интегрирования нескорректированной системы, т.е.
принимаем минимальное из постоянных времени интегрирования нескорректированной системы, т.е. 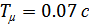 . Значит, желаемая передаточная функция будет выглядеть следующим образом:
. Значит, желаемая передаточная функция будет выглядеть следующим образом:
Wж (р) = 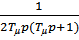 =
= 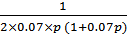 =
= 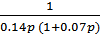
Обозначив как Wky ( p ) передаточную функцию корректирующего устройства (регулятора) и определив передаточную функцию разомкнутой системы 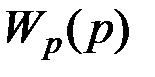 , Wky ( p )можно отыскать следующим образом:
, Wky ( p )можно отыскать следующим образом:
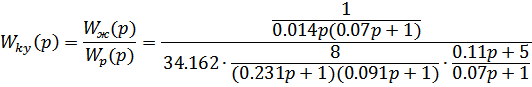
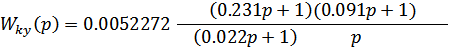
Регулятор включает в себя:
1.Пропорционально-интегрирующее звено 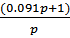
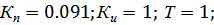
2. Инерционное дифференцирующее звено со статизмом 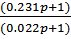
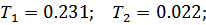
3. Пропорциональное звено 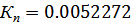
8. Моделирование переходных характеристик САУ, скорректированной на технический оптимум.
На рис.14 представлена модель скорректированной системы 
Рис.14. Схема скорректированной САУ в MatLab
1.)При отсутствии возмущений для граничных значений g .








