Виды дискретизации

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Дискретные системы.

Сигналы, действующие в системах автоматического управления, бывают непрерывными и дискретными. Соответственно этому САУ делятся на системы непрерывного и дискретного действия.
В свою очередь дискретные САУ делятся на релейные, импульсные и цифровые. Релейные САУ - это системы с квантованием по уровню, импульсные - с квантованием по времени, а цифровые - с применением обоих видов квантования.

Рис.4.1

Остановимся более подробно на импульсных САУ. Импульсная система отличается от непрерывной наличием импульсного элемента (рис.4.1). Импульсный элемент (ИЭ) представляет собой модулятор импульсов. Он преобразует непрерывно изменяющийся входной сигнал в последовательность модулированных импульсов. Будем рассматривать лишь импульсные системы первого рода, когда высота (амплитуда импульсов) изменяется в соответствии с изменением значения входной величины импульсного элемента в дискретные равноотстоящие моменты времени, т.е. когда импульсный элемент осуществляет амплитудно-импульсную модуляцию (АИМ).

Виды дискретизации

Сущность дискретизации аналоговых сигналов заключается в том, что непрерывность во времени аналоговой функции s(t) заменяется последовательностью коротких импульсов, амплитудные значения которых c_n определяются с помощью весовых функций, либо непосредственно выборками (отсчетами) мгновенных значений сигнала s(t) в моменты времени t_n.Представление сигнала s(t) на интервале Т совокупностью дискретных значений c_n записывается в виде:

(с₁, с₂, ... , c_N) = А[s(t)],

где А - оператор дискретизации. Запись операции восстановления сигнала s(t):

s'(t) = В[(с₁, с₂, ... , c_N)].

Выбор операторов А и В определяется требуемой точностью восстановления сигнала. Наиболее простыми являются линейные операторы. В общем случае:

с_n = 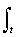q_n(t) s(t) dt, (5.1.1)

где q_n(t) - система весовых функций.

- Равномерная дискретизация. Спектр дискретного сигнала

- Дискретизация с усреднением

- Дискретизация спектров

- Дискретизация усеченных сигналов

- Соотношение спектров одиночного и периодического сигналов

- Дискретизация по критерию наибольшего отклонения

- Адаптивная дискретизация

2 Описание квантователя (-)

Для применения аппарата z-преобразования к непрерывным цепям и системам достаточно искусственной дискретизации непрерывного процесса во времени путем введения фиктивного импульсного элемента в соответствующую точку структуры. Тем самым рассматриваемая цепь или система переводится в класс квазидискретных.

При этом существует две возможности выбора места расположения фиктивного импульсного ключа, приводящие к принципиально разным результатам. Если фиктивный ключ располагается непосредственно на выходе интересующей нас величины, то это означает, что процессы в структуре с введением ключа не изменяются. В этом случае мы лишь подвергаем наблюдаемый процесс квантованию во времени, то есть вместо непрерывного сигнала рассматриваем решетчатую функцию, в точности совпадающую с истинным процессом в тактовых точках. От выбора интервала дискретности фиктивного ключа T будет зависеть лишь плотность решетчатой выборки, но не ее точность. Однако, при таком подходе возникают трудности определения корней характеристического полинома, если его степень выше второй.

3 Описание фиксатора

Поскольку форма импульсов на выходе ИЭ может быть самой разнообразной (прямоугольной, треугольной, кусочно-экспоненциальной), для единства подхода к исследованию импульсных САУ используют следующий эффективный метод их математического описания.

Импульсный элемент, формирующий на выходе последовательность импульсов определенной формы, заменяется последовательно соединенным идеализированным элементом, генерирующим модулированные 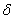-функции т.е. простейшим импульсным элементом (ПИЭ) или квантователем, и формирующим элементом (ФЭ), преобразующим последовательность 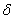-функций в последовательность импульсов заданной формы (рис. 1.9). У модулированной 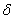-функции, как и у немодулированной, амплитуда стремится к бесконечности, а длительность – к нулю, при этом площадь импульса, сформированного ПИЭ в момент 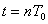, равна , то есть:

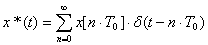. (1.5)

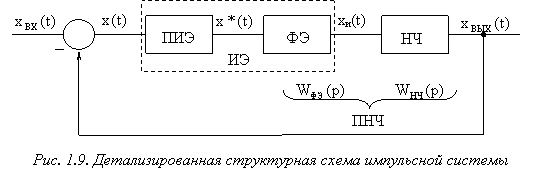
Обозначим передаточную функцию ФЭ как 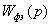, а функцию времени, описывающую импульсы на его выходе, как 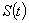. Тогда, учитывая, что выходной сигнал ФЭ представляет собой реакцию на 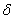-функцию, т.е. является функцией веса ФЭ, можно записать:

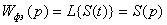, (1.6)

где 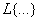– оператор преобразования Лапласа; S(p) – изображение S(t).