Экспертиза во многих практических ситуациях – это принятие решения в слабо формализованной проблеме. Целью экспертизы может быть определение числа, события, программы действий.

Дата: 2025-06-14; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

I. ЭКСПЕРТИЗА

Экспертные оценки при принятии решений в той или иной форме использовались во все времена. Дельфийский оракул в Древней Греции вещал внушаемые свыше пророчества, а совет старейшин их интерпретировал, стремясь верно определить подсказанное богами решение. Организация и проведение экспертиз, реализованных в той или иной форме, отражающей особенности эпохи, народа, традиций и обычаев, должны были обеспечить профессиональную оценку ситуаций и принятие эффективных управленческих решений. По мере совершенствования и усложнения процесса принятия решений, технологического совершенствования, возрастало внимание к экспертным оценкам.

Началом становления экспертных оценок условно считают момент создания первых официально описанных и исследованных технологий экспертного оценивания. В частности, появление в 50-е, 60-е годах ХХ века работ, посвященных групповому выбору, определению результата коллективных экспертиз, методам Делфи, мозговой атаки, сценариев и др., описанию опыта их использования. Но и до этого периода было множество работ, предшествовавших началу широкого использования экспертных оценок. В том числе и рассуждения Галилео Галилея о точности оценок экспертов, и работы Кондорсе, впервые обратившего внимание на то, что принцип большинства далеко не всегда позволяет определить наилучшую альтернативу, и работы Бернулли по субъективной вероятности и так далее.

1.1. Основные понятия

Эксперт – специалист, обладающий познаниями, навыками и опытом работы. Эксперт привлекается руководителем для оценки ситуации, анализа вариантов решения проблемы. Но принимать решение будет только руководитель. Эксперт несет ответственность за полноту своего анализа. На него не может быть возложена ответственность за последствия принятого решения.

Экспертиза во многих практических ситуациях – это принятие решения в слабо формализованной проблеме. Целью экспертизы может быть определение числа, события, программы действий.

Экспертиза позволяет получить оценки процессов (явлений), которые не поддаются непосредственному измерению. Они основаны на суждениях экспертов.

Результаты экспертизы подвергаются специальной математической обработке, которая дает возможность оценить степень надежности полученных результатов.

Экспертиза должна проводиться при обеспечении следующих условий: объективности, конфиденциальности, профессионализма, компетентности, ответственности.

Чтобы обеспечить эти условия эксперт должен быть не заинтересован в результатах экспертизы, иметь психологическую независимость и должную квалификацию. Подбор эксперта ответственная задача. Следует учитывать:

– связь профиля деятельности эксперта с анализируемой проблемой;

– совпадение рекомендаций и фактических результатов в ранее выполняемых экспертом работах;

– степень согласованности мнения эксперта с другими экспертами;

– опыт экспертной деятельности;

– квалификационный уровень эксперта;

– степень доступности эксперта к необходимой дополнительной информации.

Оценка эксперта может проводиться руководителем предприятия в виде тестового контроля. Эксперту поручается выполнить несколько экспертиз по ситуациям, имеющим предварительную объективную оценку. Сравнение мнения эксперта с известной оценкой может быть критерием его профессионализма.

Кроме того, в ходе проведения экспертизы решаются вопросы формирования экспертной группы – её численности и компетентности.

Для выбора эксперта может быть использован метод экономической оценки. Он предполагает оценку вариантов[1] по формуле:

C_i=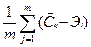

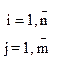
где С_i – средняя прибыль по i-му варианту проекта

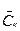– прибыль по j-ой стратегии[2] i-го варианта проекта.

Э_i – расходы на i-ый вариант экспертизы

m ­– общее число стратегий реализации проекта.

Различают методы получения количественных и качественных экспертных оценок.

1.2. Методы количественных экспертных оценок

При получении количественной информации о большом количестве объектов исследования (например, о состоянии рынка, его участниках, реакции респондентов на некое событие) используются количественные методы экспертных оценок.

В основе методик количественных исследований лежат строгие статистические модели, используются большие выборки, что в свою очередь позволяет получить высокоточные количественные (числовые) значения изучаемых показателей. Что в свою очередь дает возможность их экстраполировать (распространять, обобщать) на большие объекты (все население региона или на исследуемую группу).

На основе результатов количественных исследований можно рассчитывать необходимые объемы производства, рентабельность, формировать цену, параметры продукта, находить незанятые ниши рынка и многое другое.

Количественные исследования рекомендуется проводить:

- для определения частоты и объема потребления товара;

- при сравнении относительной эффективности нескольких готовых концепций рекламных кампаний;

- для выявления источников получения информации;

- при определении глубины проникновения товара на рынок и т.п.

Методики количественных исследований включают:

- личные интервью

- телефонные интервью

- исследования розничной сети (retail audit, store-check)

Личное интервью - это классический метод исследования, с помощью которого интервьюер получает информацию непосредственно от респондента в личной беседе, в отсутствие посторонних лиц. Персональное интервью предполагает высокую степень доверительности; при этом позволяет использовать демонстрационных материалов (карточек, фотографий, рисунков).

Телефонное интервью – индивидуальное интервью, которое проводится по телефону. Методом телефонного опроса можно собирать информацию как по физическим лицам (жителям города, потребителям определенного товара и т.п.), так и по юридическим лицам (руководители, менеджеры организаций и т.п.)

Метод стор-чек ( store cheking) предполагает обследование торговых точек - розничных и мелкооптовых, направленное на изучение ассортимента и ценовых характеристик товаров и марок; мониторинг наличия и цены различных марок в розничной и мелкооптовой сети; изучение коммерческих предложений по рекламным и деловым средствам массовой информации.

Метод используется для оценки доли локального рынка потребительских товаров, принадлежащие различным торговым маркам (производителям, дистрибьюторам, поставщикам). Позволяет получить надежные данные в ситуации отказа торговцев дать информацию о показателях своей деятельности, в том числе о:

ü ассортименте и структуре торгового предложения (по наименованиям, товарным группам, маркам, производителям, дилерам и дистрибьюторам, типам торговых точек)

ü распространенность марок;

ü различия между оптовыми и розничными ценами;

ü разброс цен на марку в розничной и оптовой торговле в зависимости от разных критериев (например, типа торговой точки, региона);

ü торговые стратегии конкурентов;

ü косвенные оценки доли рынка и объемов продаж товаров разных наименований, производителей, марок и т. д.

Store-check рекомендуется использовать в рамках комплексного анализа состояния и перспектив развития конкретного сектора рынка потребительских товаров (наряду с качественными методами, экспертными опросами, опросами потребителей).

Retail audit – это мониторинг изменений различных параметров товара (цена, ассортимент, уровень представленности в торговых точках, объемы продаж) или розничной торговли (ассортимент товаров по группам, размещение товаров в торговых помещениях, разнообразие упаковок, уровень цен конкурирующих марок и т.п.) в условиях меняющейся рыночной ситуации и учета деятельности конкурентов.

Холл-тест – специальный метод исследований, который можно отнести одновременно и к количественным, и к качественным исследованиям. По сути, холл-тест является разновидностью личных интервью, однако выносится в отдельную категорию в силу своей популярности. Метод подразумевает проведение интервью с респондентами в специально отведенном для этого помещении с целью тестирования определенных свойств продукта (вкус, запах, цвет, упаковка, дизайн) или рекламных материалов. Помещения для холл-тестов оборудованы для тестирования товаров, моделирования ситуации потребительского выбора и просмотра рекламы.

Методы получения количественных оценок:

– непосредственная количественная оценка,

– метод средней точки,

– метод Черчмена-Акофа,

– метод лотерей.

Непосредственная количественная оценка используется для определения значения показателя, измеряемого количественно, или для оценки степени сравнительной предпочтительности различных объектов[3].

Метод средней точки используется для оценки большого числа вариантов. Метод итерационной. Каждый следующий, подлежащий оценке вариант а_{i+ k}, удовлетворяет уравнению:

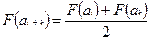
Процедура завершается, когда определяется сравнительная предпочтительность альтернативных вариантов.

Метод Черчмена-Акофа используется при количественной оценке альтернативных вариантов. Допускает корректировку экспертных оценок. В методе предполагается, что:

– если F(a₁) > F (a₂), то а₁ – предпочтительнее a₂,

– оценка одновременной реализации вариантов i и j равна F(a_i) + F (a_j),.

Варианты ранжируются по предпочтительности. При этом:

1) если а₁ предпочтительнее прочих вариантов, то

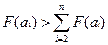и а₁ из дальнейших рассмотрений исключается

иначе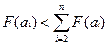

2) если а₁ менее предпочтителен, чем сумма прочих вариантов, то

F(a₁) сравнивается с .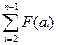

Метод лотерей. По этому методу, для любой тройки вариантов а₁, а₂, а₃, упорядоченных в порядке убывания предпочтительности, эксперт указывает такую вероятность р, при которой вариант а₂ равноценен лотерее, при которой вариант а₁ встречается с вероятностью р, а вариант а₃ – с вероятностью (1-р).

На основании последовательной сравнительной оценки нескольких троек вариантов рассчитываются числа u₁, u₂, …, u_n, с помощью которых формируется линейная функция полезности:

u₁р₁+ u₂p₂+ … u_np_n,

где р₁, p₂ , …, p_n – вероятности, с которыми рассматриваются варианты а₁, а₂, а_n.

Эта формула позволяет сравнивать по предпочтительности различные лотереи, характеризующиеся различными вероятностями реализации альтернативных вариантов а₁, а₂,…, а_n.

1.3. Методы качественных экспертных оценок

В случае ограниченных возможностей применения математических методов, отсутствия достаточно точной статистической и другой информации об исследуемых показателях, применяют методы качественных экспертных оценок.

Методы получения качественных экспертных оценок:

– экспертная классификация,

– метод парных сравнений,

– ранжирование альтернативных вариантов,

– метод векторов предпочтений,

– дискретные экспертные кривые.

Экспертная классификация используется, когда необходимо определить принадлежность оцениваемых вариантов к установленным и принятым к использованию классам, категориям, уровням, сортам и т.д.

Он используется, когда конкретные классы, к которым должны быть отнесены оцениваемые объекты, заранее не определены (или не определено число классов, на которое производится разбиение оцениваемых объектов).

Если эксперту необходимо отнести каждый из вариантов к одному из заранее установленных классов, то используется процедура последовательного предъявления эксперту вариантов. Эксперт определяет к какому из классов принадлежит объект.

После завершения этой процедуры эксперту может быть предъявлен результат его оценки и представляется возможность внести коррективы.

Если проводится коллективная экспертиза, то результаты экспертной классификации, указанные каждым из экспертов, обрабатываются с целью получения результирующей коллективной оценки.

Если число классов, на которое должны быть разбиты варианты, заранее не оговаривается, то целесообразно использовать следующие процедуры:

– эксперту предъявляется пара вариантов и предлагается определить, относятся ли они к одному классу или к разным;

– эксперту последовательно предлагаются оцениваемые варианты и выясняется, может ли каждый из них быть отнесен к одному из образовавшихся к тому времени классов или необходимо для данного варианта образовать новый класс.

Процедура завершается после того, как эксперту будут предъявлены все варианты.

Метод парных сравнений. Эксперту последовательно предлагаются пары альтернативных вариантов, из которых он должен указать более предпочтительный. Если эксперт затрудняется сделать выбор, он вправе посчитать сравниваемые варианты равноценными либо несравнимыми. После последовательного предъявления эксперту всех пар вариантов определяется их сравнительная предпочтительность по оценкам данного эксперта. В результате парных сравнений, если эксперт оказался последовательным в своих предпочтениях, все оцениваемые варианты могут оказаться проранжированными по тому или иному критерию (показателю, свойству). Если эксперт признал некоторые варианты несопоставимыми, то в результате будет получено лишь их частичное упорядочение.

При достаточно большом числе оцениваемых вариантов, процедура парного сравнения всех возможных их пар становится трудоемкой для эксперта. В этом случае целесообразно применение соответствующих модификаций метода парных сравнений. Например, если предположить непротиворечивость оценок эксперта, то практически достаточно однократного предъявления каждого альтернативного варианта в паре с каким-либо другим.

Ранжирование вариантов. При решении многих практических задач часто бывает необходимо расположить некоторые факторы или альтернативы в порядке возрастания или убывания их по какому-либо присущему им свойству. Это называется ранжированием. Оно применяется в следующих случаях:

– когда необходимо упорядочить явления (объекты) во времени и пространстве;

– если нужно упорядочить объекты в соответствии с их каким-либо измеримым качеством, но при этом не требуется производить его точное измерение;

– когда какое-либо качество в принципе измеримо, но в данный момент по какой-либо причине не может быть измерено.

При ранжировании каждый участник должен расположить объекты (альтернативы) в порядке, который представляется ему наиболее рациональным, и приписать каждому из них числа натурального ряда – ранги. При этом ранг 1 получает наиболее предпочтительная альтернатива, а ранг n – наименее предпочтительная.

Следовательно, порядковая шкала, получаемая в результате ранжирования, должна удовлетворять условию равенства числа рангов n числу ранжируемых объектов.

Сумма рангов S_n должна быть равна сумме чисел натурального ряда:

S_{n = ,}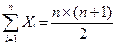

где X_i – ранг i-го объекта.

Эксперту предъявляются отобранные для сравнительной оценки варианты, но желательно не более 20-30 для их упорядочения по предпочтительности.

Если вариантов больше, то целесообразно использование соответствующих модификаций метода ранжирования. Ранжирование сравниваемых объектов эксперт может осуществлять различными способами.

После проведения экспертной оценки проводят анализ согласованности ответов экспертов. Если экспертная группа состоит всего из двух человек, то оценку согласованности их ответов можно провести по коэффициенту ранговой корреляции Спирмена p.

p = 1 – ,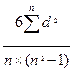

где: d – разность между рангами пар оценок экспертов;

n – число сопоставляемых пар.

Если число экспертов больше двух, оценка степени согласованности их мнений производится с помощью коэффициента конкордации W:

W = 12S/m³ (n³– n),

где: m – число экспертов в группе;

n – число ранжируемых объектов (факторов, альтернатив):

S = .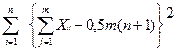

В случае, когда какой-либо эксперт не может установить ранговое различие между несколькими объектами и присваивает им одинаковые ранги, расчет коэффициента W производится по формуле:

W = ,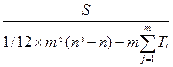

T_j = 1/12 ,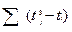

где t – число одинаковых рангов в j-м ряду.

Для проверки значимости W используется распределение 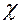² c (n-1) степенями свободы и уровнем значимости 0,01 или 0,05:

.

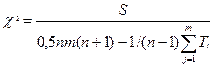Метод векторов предпочтений. Используется при коллективном экспертном ранжировании. Эксперту предъявляется весь набор оцениваемых вариантов и предлагается для каждого варианта указать сколько вариантов превосходит данный.

Эта информация предоставляется в виде вектора. Первая компонента его – число вариантов, которые превосходят первый. Вторая компонента – число вариантов, которые превосходят второй, и т.д.

Если в векторе предпочтений каждое число встречается ровно один раз, то экспертом указано строгое ранжирование вариантов по предпочтениям. В противном случае полученный результат не является строгим ранжированием и отражает затруднения эксперта при оценке сравнительной предпочтительности отдельных вариантов. Метод векторов предпочтений сравнительно не трудоёмок.

При коллективной экспертизе, проводимой с использованием метода векторов предпочтений, целесообразно рассчитать результирующие коллективное ранжирование, отражающее коллективную точку зрения всех экспертов.

Дискретные экспертные кривые. Если целью является разработка прогнозов или анализ динамики изменения показателей, характеризующих объект, то целесообразно воспользоваться дискретными экспертными кривыми.

При построении дискретной экспертной кривой определяется набор характерных точек, в которых наблюдается (или ожидается) смена тенденций поведения показателя, а также значения показателя в характерных точках. На участках между характерными точками предполагается, что значение показателя изменяется линейно, т.е. две соседние характерные точки кривой могут быть соединены отрезками прямой линии.

Для того, чтобы определить нелинейные изменения значений показателя на участках кривой между соседними характерными точками дискретных экспертных кривых переходит к экспертным оценкам.

Использование экспертных кривых позволяет наглядно представить различные сценарии развития ситуации, что необходимо при разработке прогнозов.

1.4. Методы комплексной экспертной оценки

Это метод сумм, метод бальной оценки, метод расстояний. Они используются для оценки “n” объектов по “m” показателям (например, по оценкам объекта, данным различными экспертами).

Метод сумм. Для каждого объекта рассчитывается обобщенной показатель:

П_i = 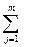p_j * a_ij,

где p_j – весовой коэффициент для j-го показателя;

a_ij– значение j-го показателя для i-го объекта;

П_i – обобщенный показатель для i-го объекта.

Чем предпочтительнее объект, тем больше значение его обобщенного показателя.

Метод бальной оценки. Баллы, приписываемые исходным показателям, могут быть получены:

– на основе предварительных соглашений;

– на основе ранжирования показателей объекта.

Далее, к таблице баллов применяется метод сумм (см. приложение 1).

Метод расстояний. Объект рассматривается как точки в m-мерном пространстве: координаты точки – значения показателей. Расстояние от этой точки до точки-эталона определяет место объекта в исследуемой совокупности и равно:

П’_i = ( 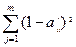p_j) ,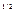

где p_j 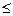1– весовой коэффициент для j-го показателя;

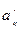= a_ij / a_oj,

a_ij– значение j-го показателя для i-го объекта;

a_oj– значение j-го показателя для объекта эталона;