Тема урока: «Соотношения между сторонами и углами треугольника»

Дата: 2025-06-14; Просмотры: 11

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

07.04.2023 Геометрия 7

Тема урока: «Соотношения между сторонами и углами треугольника»

Цель урока: повторить и обобщить знания, умения и навыки учащихся по теме «Соотношения между сторонами и углами треугольника»; формирование навыков применения полученных знаний при решении задач.

Тип урока: обобщение и систематизация знаний, умений и навыков учащихся..

Ход урока

I . Организационный момент

II . Устная работа.

1) Найдите неверные утверждения и исправьте их. (Обоснуйте ответ)

- В любом треугольнике два угла – острые(верно)

- Существует треугольник с двумя прямыми углами (неверно)

- Если один из углов тупой, то треугольник тупоугольный (верно)

- Сторона прямоугольного треугольника, лежащая против прямого угла, называется катетом (неверно)

- Существует треугольник с двумя тупыми углами (неверно)

- Существует треугольник с углами 60⁰, 90⁰ и 45⁰ (неверно)

- Существует треугольник со сторонами 4 см., 4 см. и 9 см. (неверно)

- Существует треугольник со сторонами 4 см., 6 см. и 9 см (верно)

- В равнобедренном треугольнике углы при основании могут быть тупыми (неверно)

- В равнобедренном треугольнике углы при основании равны (верно)

- В треугольнике против меньшей стороны лежит больший угол (неверно)

- В прямоугольном треугольнике гипотеза больше любого катета (верно)

- В треугольнике против меньшей стороны меньший больший угол (верно)

- Треугольник, у которого два угла равны 25⁰ и 55⁰ – остроугольный (неверно)

- Треугольник, у которого два угла равны 19⁰ и 71⁰ – прямоугольный (верно)

III . Решение задач.	В ходе решения учащиеся повторяют определение внешнего угла, теорему о внешнем угле,определение смежных углов, теорему о соотношениях между сторонами и углами треугольникаотрабатывают навыки применять полученные знания при решении задач.
№1. Найдите внешние углы треугольника, если известны два его внутренних угла: 250 и 730. Сравните стороны ВС и АС. С В А Е F D 73 0 25 0 3 1 2
Дано: ∆АВС, С = 250, В = 730 _____________________ а) найти FАС, АВD, ВСЕ; б) сравнить ВС и АС.	Решение:     а)Обозначим внутренние углы ∆АВС: А = 1, В = 2, С = 3. FАС = 2 + 3 = 730 + 250 = 980(по теореме о внешнем угле). 1 = 1800 – ( 2 + 3) = 1800 – 980 = 820 (по теореме о сумме углов треугольника). ВСЕ = 1 + 2 = 820 + 730 = 1550 (по теореме о внешнем угле). Аналогично, АВD = 1 + 3 = 820 + 250 = 1070. б)Т.к. 1 = 820, 2 = 730, то ВС >АС (неравенство треугольника) Ответ: 980, 1070, 1550.
№2.В треугольнике ABC В= 90° , А = 60° . На катете ВС отложен отрезок ВО, равный ВА.Найдите углы треугольника АОС.
Дано: ∆АВС, В= 90° , А = 60°, ВО = ВА. ________________________ Найдите углы ∆ АОС.	Решение: 600 О С А В     1)В ∆АВС найдем С. С = 1800– ( В + А) = 300 (по теореме о сумме углов треугольника) или т.к. ∆АВС–прямоугольный ( В = 90°), то А + С = 900. Следовательно, С = 300 (по свойству прямоугольного треугольника).   2) Рассмотрим ∆АВО. ∆АВО – равнобедренный, т.к. ВО = ВА (по определению равнобедренного треугольника). 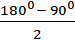Следовательно, А = О = = 450 (по теореме о сумме углов треугольника) 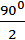или   А= О = = 450 (по свойству прямоугольного треугольника).   3) ОАС = ВАС – ВАО = 600– 450 = 150.   4) Найдем АОС. Из ∆АОС АОС = 1800– (300 +150) = 1350(по теореме о сумме углов треугольника) или АОС – внешний угол ∆АВО. АОС = ВАО + АВО = 450 +900 = 1350 (по теореме о внешнем угле треугольника) или АОС+ АОВ = 1800 (смежные). Следовательно, АОС = 1800–450 = 1350.   Ответ: 300, 150, 1350.