Тема урока: «Формула суммы n первых членов арифметической прогрессии»

Дата: 2025-06-14; Просмотры: 8

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Девизом нашего урока будут слова русского математика В.П. Ермакова: «В математике следует помнить не формулы, а процессы мышления».

Ход урока

Постановка проблемы

На доске- портрет Гаусса. Учитель или ученик, которому заранее было дано задание подготовить сообщение, рассказывает, что когда Гаусс учился в школе, учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за минуту.

Вопрос. Как Гаусс получил ответ?

Поиск путей решения

Учащиеся высказывают свои предположения, затем подводится итог: сообразив, что суммы 1+100, 2+99 и т.д. равны, Гаусс умножил 101 на 50, то есть на число таких сумм. Иначе говоря, он заметил закономерность, которая присуща арифметической прогрессии.

Вывод формулы суммы n первых членов арифметической прогрессии

Записать на доске и в тетрадях тему урока. Ученики вместе с учителем записывают вывод формулы:

Пусть а₁;а₂; а₃; а₄;….;а_n-2; а_n-1; а_n- арифметическая прогрессия.

S_n=a₁+a₂+a₃+…a_n-1 + a_n

+

S_n=a_n + a_n-1 + a_n-2 +…+ a₂ + a₁

2S_n=(a₁ + a_n )+ (a₂+ a_n-1)+ (a_n-1 + a₂ )+ (a_n + a₁)

a₂ + a_n-1 + a₁ + d+ a_n-d= a₁ + а _n ,

a₃ + a_n-2 = a₂ + d+ a_n-1 -d= a₂ + a_n-1 = a₁ + a_n ,

…

2S_n= (a₁+a_n)n,

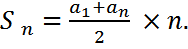
Первичное закрепление

1. Решим, используя формулу (1), задачу Гаусса:

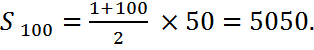
2. Используя формулу (1), решить задачи (а _n )- арифметическая прогрессия:

а ) a₁=2, a₁₀ =20. S₁₀ -? [110]

б ) a₁=-5, a₇ =1. S₇ -? [-14]

в ) a₁=2, a₆ =-17. S ₆ -? [-57]

г) a₁=-5, a₁₁ =5. S₁₁ - ? [0]

3. Выполнить задание №603( а)

Дано: (а _n ) – арифметическая прогрессия;

a ₁ =3, a ₆₀ =57.

Найти: S ₆₀ .

Решение. Воспользуемся формулой суммы n первых членов арифметической прогрессии

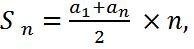
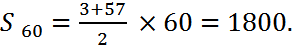
Ответ: 1800.

Дополнительный вопрос. Сколько типов различных задач можно решить по этой формуле?

Ответ. Четыре типа задач:

- найти первый член арифметической прогрессии а _n ;

- найти количество членов арифметической прогрессии.

4. Выполнить задание №603(б).

Найти сумму шестидесяти первых членов арифметической прогрессии (а _n ), если а₁₌ -10,5, а₆₀ = 51,5.

Решение.

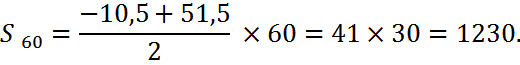
Ответ: 1230.

Дополнительный вопрос. Запишите формулу n-го члена арифметической прогрессии.

Ответ : a_n = a₁ + d (n-1).

Выполнить № 605 (а)

5.Вычислите формулу девяти первых членов арифметической прогрессии ( b_n ) если b ₁ =-17, d =6.

-Можно ли вычислить сразу, используя формулу?

- Нет, так как неизвестен девятый член.

-Как его найти?

- По формуле n-го члена арифметической прогрессии.

Решение. b ₉ = b ₁ +8 d =-17+8 6=31;

.

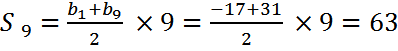Ответ.63.

Вопрос. А нельзя ли найти сумму, не вычисляя девятого члена прогрессии?

Постановка проблемы

Проблема: получить формулу суммы n первых членов арифметической прогрессии, зная ее первый член и разность d.

(Вывод формулы у доски учеником.)

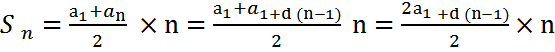. (2)

Решим №371 (а) по новой формуле (2):

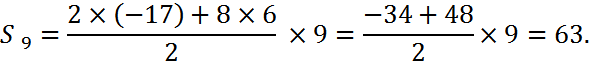
Устно закрепим формулы (2).

( a_n )- арифметическая прогрессия.

а) a ₁ =3, d =4. S₄ -? [36]

б) a₁ = 2 , d = -5 . S₃ -? [-9]

Самостоятельная работа

Вариант 1

Дано: ( a_n )- арифметическая прогрессия.

а) a₁ =-3, а₆ =21. S ₆ -? [ 54 ]

б) a₁ =6, d = - 3. S ₄ -? [6]

Вариант 2

Дано: ( a_n )- арифметическая прогрессия.

а) a₁ =2, а₈ =-23. S ₈ -? [ -84 ]

б) a₁ =-7, d =4. S ₅ -? [5]