Сумма углов треугольника.
02. 02. 2023 г. 7 класс Геометрия.
Сумма углов треугольника.
Свойства углов треугольника
Треугольник – это центральная фигура геометрии. Он обладает многими удивительными свойствами. Два этих свойства, касающихся углов, мы сейчас повторим.
Пусть дан треугольник 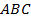 с внутренними углами
с внутренними углами 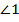 ,
, 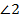 ,
, 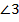 .
.
Теорема утверждает, что сумма внутренних углов треугольника равна 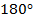 (см. Рис. 1).
(см. Рис. 1).
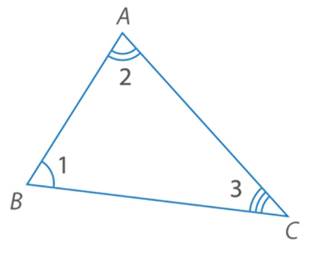
Рис. 1. Иллюстрация к теореме о внутренних углах треугольника
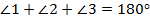
Это теорема о внутренних углах треугольника.
Следующая теорема о внешнем угле треугольника.
Внешний угол треугольника равен сумме двух других внутренних углов, не смежных с ним (см. Рис. 2).
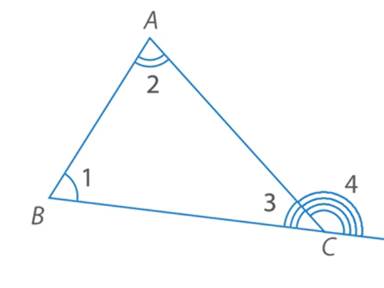
Рис. 2. Иллюстрация к теореме о внешнем угле треугольника
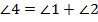
Из того, что сумма внутренних углов треугольника 180 градусов, вытекает наличие трех видов треугольников.
Виды треугольников
Первый – это остроугольный треугольник 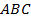 .
.
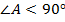 ,
, 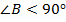 ,
, 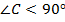
Например: (см. Рис. 3).
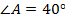
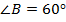
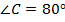
В сумме углы составляют 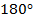 , каждый из них меньше
, каждый из них меньше 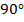 .
.
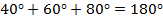
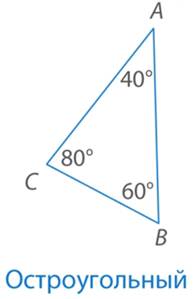
Рис. 3. Остроугольный треугольник
Тупоугольный треугольник (см. Рис. 4)
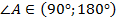 – угол
– угол 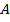 тупой, т. е. лежит в пределах от 90 градусов до 180 градусов.
тупой, т. е. лежит в пределах от 90 градусов до 180 градусов.
Например:
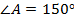
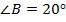
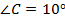
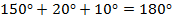
Тупым может быть только один угол.
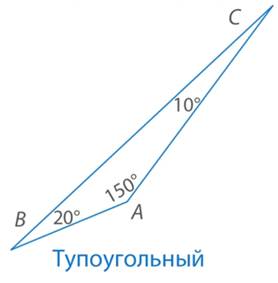
Рис. 4. Тупоугольный треугольник
Прямоугольный треугольник (см. Рис. 5)
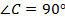 ,
, 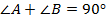
Например:
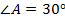
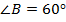
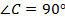
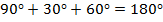
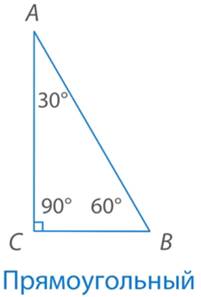
Рис. 5. Прямоугольный треугольник
Таким образом, мы рассмотрели все виды треугольников.
Теперь рассмотрим некоторые типовые задачи на углы треугольника.
Задача 1
Найдите угол 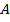 треугольника
треугольника 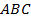 , если угол
, если угол 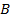 равен 60 градусов, угол
равен 60 градусов, угол 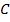 равен 50 градусов (см. Рис. 6).
равен 50 градусов (см. Рис. 6).
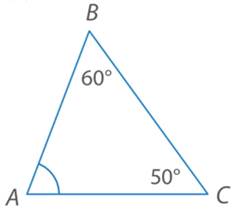
Рис. 6. Иллюстрация к задаче 1
Дано:
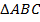 ,
, 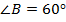 ,
, 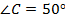 .
.
Найти: 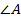 .
.
Решение
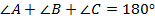
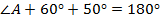
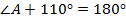
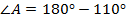
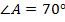
Ответ: 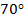 .
.
Здесь мы воспользовались теоремой о внутренних углах треугольника.
Задача 2
Доказать, что углы при основании равнобедренного треугольника – острые (см. Рис. 7).
Дано: 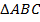 ,
, 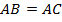 .
.
Доказать: 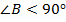 ,
, 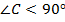 .
.
Доказательство
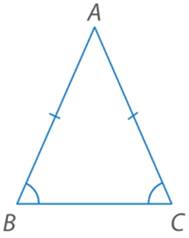
Рис.7. Иллюстрация к задаче 2
В равнобедренном треугольнике углы при основании равны (по свойству равнобедренного треугольника): 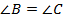 .
.
Пусть 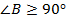 , тогда
, тогда 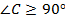
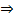
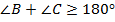 . Это противоречит тому, что
. Это противоречит тому, что 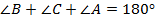 .
.
Что и требовалось доказать.
В предыдущих задачах фигурировали только внутренние углы треугольника. В следующей задаче присутствует внешний угол треугольника.
Задача 3
Найдите углы в треугольнике 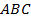 , если
, если 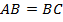 , внешний угол при вершине
, внешний угол при вершине 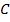 равен 100 градусам (см. Рис. 8).
равен 100 градусам (см. Рис. 8).
Дано: 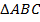 ,
, 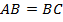 ,
, 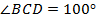 .
.
Найти: 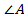 ,
, 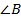 ,
, 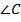 .
.
Решение
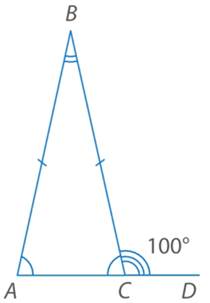
Рис. 8. Иллюстрация к задаче 3
Данный треугольник равнобедренный по условию.
Вспомним, что внешний угол 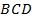 и внутренний угол
и внутренний угол 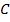 – смежные углы и в сумме осоставляют
– смежные углы и в сумме осоставляют 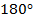 . Один из них дан, значит, можно найти другой, а если треугольник равнобедренный, то углы при основании равны
. Один из них дан, значит, можно найти другой, а если треугольник равнобедренный, то углы при основании равны 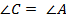 , а, зная эти два угла, мы можем найти и третий угол.
, а, зная эти два угла, мы можем найти и третий угол.
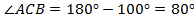
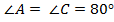
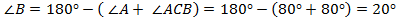
Ответ: 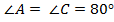 ;
; 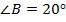 .
.
Задача 4
Найти сумму углов при всех вершинах пятиконечной звезды (см. Рис. 9).
Дано: 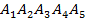 – звезда.
– звезда.
Найти: 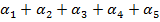 .
.
Решение
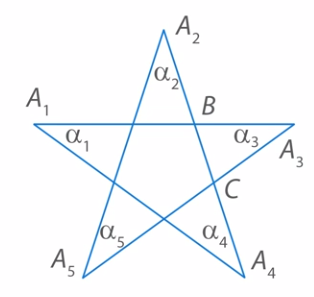
Рис. 9. Иллюстрация к задаче 4
Рассмотрим треугольник 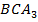 . В этом треугольнике угол при вершине
. В этом треугольнике угол при вершине 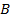 равен
равен 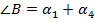 , так как угол
, так как угол 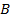 в этом треугольнике – внешний для треугольника
в этом треугольнике – внешний для треугольника 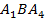 .
.
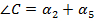 по той же теореме для треугольника
по той же теореме для треугольника 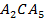 .
.
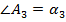
При сложении всех трех углов треугольника получим:
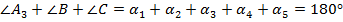
Значит искомая сумма равняется 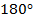 .
.
Ответ: 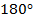 .
.
Примечание: данная сумма верна для пятиконечной звезды любой формы, с любыми углами.








