Тема: «Сложение и вычитание дробей с одинаковыми и разными знаменателями»

Дата: 2025-06-14; Просмотры: 6

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

01.06.2022 г. Урок по алгебре 8 класс.

Тема: «Сложение и вычитание дробей с одинаковыми и разными знаменателями»

Цели:

Задачи:

Развивающие:

• развивать логическое мышление;
• развивать умение контролировать свои действия;
• обучение действию по аналогии;
• развивать культуру речи;
• вырабатывать умение общения.
• познавательную активность учащихся; навыки мыслительных операций сравнение, обобщение на протяжении урока;

Образовательные:

• повторить теоретический материал по теме: «алгебраические дроби»;
• повторить способ сложения и вычитания алгебраических дробей с одинаковыми и разными знаменателями;
• закрепить навыки сложения и вычитания алгебраических дробей с разными знаменателями;
• расширять кругозор учащихся.
• обеспечение усвоения образовательных стандартов.
• развитие сотрудничества У-У.
• осуществлять оперативный контроль процесса обучения.

Воспитательные:

• вырабатывать умение преодолевать трудности ;
• прививать интерес к предмету на основе связи с жизнью и практикой;
• формировать умения высказывать свои мысли, слушать других, вести диалоги, отстаивать свою точку зрения;
• формировать навыки самооценки;
• добиться сознательного усвоения материала;

III. Изучение нового материала (основные понятия)

При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями складываются (вычитаются) их числители, а знаменатель остается тем же.

Пример 1

Сложим и вычтем дроби 5/9 и 2/9. По приведенному правилу получаем: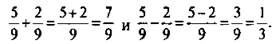

По тому же правилу складывают и любые дроби с одинаковыми знаменателями, т. е. 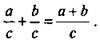Докажем, что это равенство верно при любых допустимых значениях переменных, т. е. при с ≠ 0.

Пусть 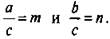Почленно сложим эти равенства и получим 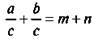или 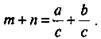По определению частного из равенства a/c = m получаем a = cm, из равенства b/c = n имеем b = сn. Почленно сложив равенства а = cm и b = сn, получим а + b = сm + сn = с(m + n). Так как с ≠ 0, то выразим из этого равенства 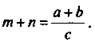Итак, имеем два равенства 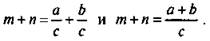Приравняв правые части этих равенств, получим 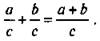Таким образом, получено тождество, из которого следует правило сложения дробей с одинаковыми знаменателями. Итак, чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же. Это правило справедливо при сложении любого числа дробей.

Пример 2

Сложим дроби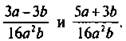

В соответствии с приведенным правилом получаем: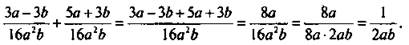

Пример 3

Спожим дроби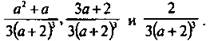

Еще раз используем правило сложения дробей и получим: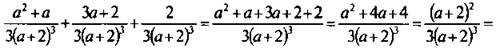

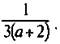
Вычитание дробей с одинаковыми знаменателями выполняется аналогично сложению. Докажем, что при любых значениях а, b и с ≠ 0 выполняется тождество 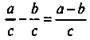. Учтем, что операция вычитания обратна по отношению к сложению. Поэтому достаточно доказать, что сумма дробей 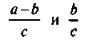равна дроби a/c. Проверим это: 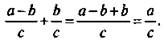Из доказанного тождества 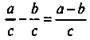следует правило вычитания дробейс одинаковыми знаменателями.

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

Пример 4

Вычтем из дроби 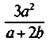дробь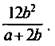

Применим приведенное правило вычитания дробей и получим: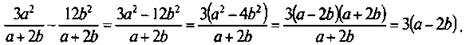

Иногда при выполнении сложения или вычитания дробей приходится изменять знак знаменателя одной из дробей и заменять операцию сложения операцией вычитания (или наоборот).

Пример 5

Сложим дроби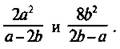

Учтем, что знаменатели дробей являются противоположными выражениями. Поэтому изменим знаки в знаменателе второй дроби и перед этой дробью (это соответствует умножению числителя и знаменателя дроби на число -1 в соответствии с основным свойством дроби). Получим: 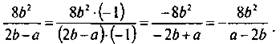После этого сложение данных дробей сводится к вычитанию дробей с одинаковыми знаменателями. Тогда имеем: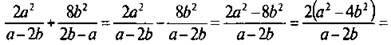

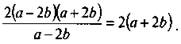
Разумеется, правила сложения и вычитания дробей в ряде случаев удобно использовать совместно.

Пример 6

Упростим выражение: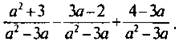

Применим совместно правила сложения и вычитания дробей с одинаковыми знаменателями и получим: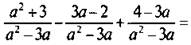

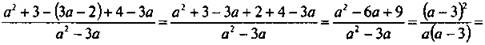
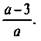
Данное выражение имеет смысл при тех значениях а, при которых знаменатель а(а - 3) ≠ 0, т. е. при а ≠ 0 и а ≠ 3.

IV. Контрольные вопросы

1. Как складывают дроби с одинаковыми знаменателями?

2. Докажите тождество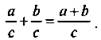

3. Как вычитаются дроби с одинаковыми знаменателями?

Чтобы складывать и вычитать алгебраические дроби с разными знаменателями, проведём аналогию с обыкновенными дробями и перенесём её на алгебраические дроби.

Рассмотрим простейший пример для обыкновенных дробей.

Пример 1. Сложить дроби: .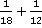

Решение:

Вспомним правило сложения дробей. Для начала дроби необходимо привести к общему знаменателю. В роли общего знаменателя для обыкновенных дробей выступает наименьшее общее кратное (НОК) исходных знаменателей.

Определение

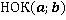– наименьшее натуральное число, которое делится одновременно на числа 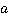и .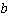

Для нахождения НОК необходимо разложить знаменатели на простые множители, а затем выбрать все простые множители, которые входят в разложение обоих знаменателей.

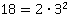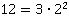; . Тогда в НОК чисел 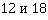должны входить две двойки и две тройки: .

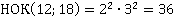После нахождения общего знаменателя, необходимо для каждой из дробей найти дополнительный множитель (фактически, поделить общий знаменатель на знаменатель соответствующей дроби).

.

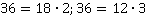Затем каждая дробь умножается на полученный дополнительный множитель. Получаются дроби с одинаковыми знаменателями, складывать и вычитать которые мы научились на прошлых уроках.

Получаем: .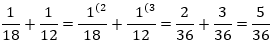

Ответ: .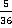

Рассмотрим теперь сложение алгебраических дробей с разными знаменателями. Сначала рассмотрим дроби, знаменатели которых являются числами.

Сложение и вычитание алгебраических дробей с разными знаменателями

Пример 2. Сложить дроби: .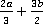

Решение:

Алгоритм решения абсолютно аналогичен предыдущему примеру. Легко подобрать общий знаменатель данных дробей: 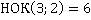и дополнительные множители для каждой из них.

.

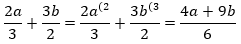Ответ: .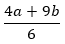

Итак, сформулируем алгоритм сложения и вычитания алгебраических дробей с разными знаменателями:

1. Найти наименьший общий знаменатель дробей.

2. Найти дополнительные множители для каждой из дробей (поделив общий знаменатель на знаменатель данной дроби).

3. Домножить числители на соответствующие дополнительные множители.

4. Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.

Рассмотрим теперь пример с дробями, в знаменателе которых присутствуют буквенные выражения.

Пример 3. Сложить дроби: .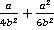

Решение:

Поскольку буквенные выражения в обоих знаменателях одинаковы, то следует найти общий знаменатель для чисел 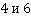. Итоговый общий знаменатель будет иметь вид: 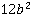. Таким образом, решение данного примера имеет вид:.

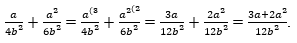
Ответ:.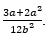

Пример 4. Вычесть дроби: .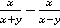

Решение:

Если «схитрить» при подборе общего знаменателя не удаётся (нельзя разложить на множители или воспользоваться формулами сокращённого умножения), то в качестве общего знаменателя приходится брать произведение знаменателей обеих дробей.

.

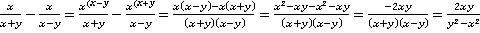Ответ: .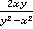

Вообще, при решении подобных примеров, наиболее сложным заданием является нахождение общего знаменателя.

Пример вычитания алгебраических дробей с разложением знаменателя на множители

Рассмотрим более сложный пример.

Пример 5. Упростить: .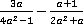

Решение:

При нахождении общего знаменателя необходимо прежде всего попытаться разложить знаменатели исходных дробей на множители (чтобы упростить общий знаменатель).

В данном конкретном случае:

;

.

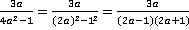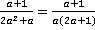Тогда легко определить общий знаменатель: .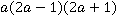

Определяем дополнительные множители и решаем данный пример:

.

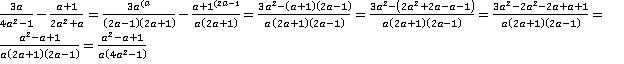Ответ: .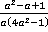

Примеры на закрепление правил сложения и вычитания алгебраических дробей с разными знаменателями

Теперь закрепим правила сложения и вычитания дробей с разными знаменателями.

Пример 6. Упростить: .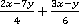

Решение:

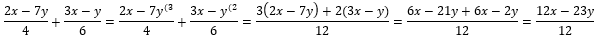
Ответ: .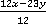

Пример 7. Упростить: .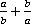

Решение:

.

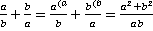Ответ: .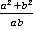

Пример сложения трёх алгебраических дробей с разными знаменателями

Рассмотрим теперь пример, в котором складываются не две, а три дроби (ведь правила сложения и вычитания для большего количества дробей остаются такими же).

Пример 8. Упростить: .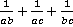

Решение:

.

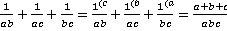Ответ: .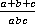

Пример вычитания алгебраических дробей с предварительным сокращением

Теперь рассмотрим пример, в котором необходимо сначала сократить дроби, а затем уже их складывать (вычитать).

Пример 9. Упростить: .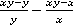

Решение:

Рассмотрим первую дробь:

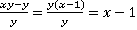. При этом следует указать, что .

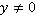Проведём аналогичные преобразования со второй дробью:

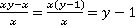. При этом следует указать, что .

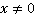Таким образом, получаем следующее преобразование:

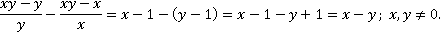
Ответ: .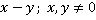

На данном уроке мы повторили правила сложения и вычитания дробей с разными знаменателями, а также решили типовые несложные задачи с использованием этих правил.

Домашняя работа. Повторить п. 3,4, правила сложения и вычитания дробей с одинаковыми и разными знаменателями, формулы сокращённого умножения.
Посмотреть видеоуроки , проработать учебный материал в файле . Решить задания "Якласс".