Характеристики качества систем M / M / V / W
Министерство образования и науки РФ
ГОУ ВПО
Воронежский ГАСУ
Кафедра Прикладной информатики и информационных систем
Отчет по лабораторной работе №5
По дисциплине: «Теория информационных процессов и систем»
Выполнил: Дудкин И.С.
Студент гр.2341Б
Принял:Сысоев Д.В.
Воронеж 2013
Цель работы:
Изучить второе распределение Эрланга и характеристики качества систем с очередями.
Второе распределение Эрланга
Характеристики качества систем M / M / V / W
V- канальная СМО обслуживает простейший поток вызовов. При занятости всех v выходов поступивший вызов становится в очередь и обслуживается после некоторого ожидания. Общее число вызовов, находящихся в системе на обслуживании и в очереди, обозначим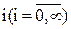 
и назовем состоянием системы. При 
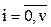величина i характеризует число занятых каналов в системе, при 
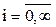число занятых каналов равно v, а разность i - v есть длина очереди. Параметр потока освобождений определяется числом занятых выходов и в первом случае 
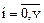зависит от состояния системы i, а во втором 
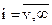имеет постоянное значение v.
Рис. Граф состояний СМО с ожиданием
Отметим, что при интенсивности поступающей нагрузки L, равной или большей числа выходов системы v, с вероятностью 1 постоянно будут заняты все выходы и длина очереди будет бесконечной. Поэтому, чтобы система могла функционировать нормально и очередь не росла безгранично, необходимо выполнить условие L < v.
Вероятность того, что система в установившемся режиме находится в состоянии i (Pi.) определяем по второму распределению Эрланга:
, 
;
, 
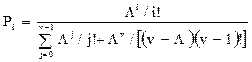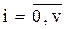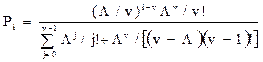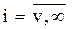
К основным характеристикам качества обслуживания СМО с ожиданием относят:
Вероятность ожидания для поступившего вызова
Для простейшего потока вызовов она совпадает с вероятностью занятости всех выходов в системе, т. е. с вероятностью потерь по времени: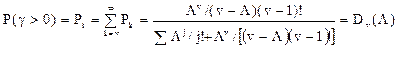 
Приведенное выражение называется второй формулой Эрланга.
Интенсивност ь обслуженной нагрузки
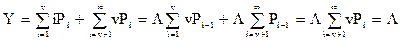
Из-за отсутствия явных потерь сообщений интенсивность поступающей нагрузки совпадает с интенсивностью обслуженной и избыточная нагрузка отсутствует. Поскольку для простейшего потока интенсивность потенциальной нагрузки равна интенсивности поступающей, потерянная нагрузка также отсутствует. Однако не всегда в системе с ожиданием потери по нагрузке равны нулю. При обслуживании примитивного потока (данная модель здесь не рассматривается) источник за счет ожидания в среднем меньше находится в свободном состоянии, чем в системе без потерь. Это приводит к снижению интенсивности потока вызовов и поступающая нагрузка меньше потенциальной. И хотя все поступающие вызовы обслуживаются, потери по нагрузке имеют место.
L можно рассматривать как математическое ожидание числа занятых выходов, а v - L -соответственно как математическое ожидание числа свободных выходов.