3-я пара: f (x); подынтегральная функция.
4-я пара: а; верхний предел интегрирования;
5-я пара: b; нижний предел интегрирования;
))
Интеграл 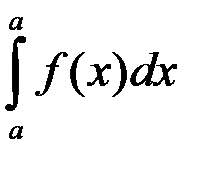 равен:
равен:
1. 2a; 2. a;
+3. 0; 4. - a.
))
Функция f (x) является нечётной. Тогда интеграл 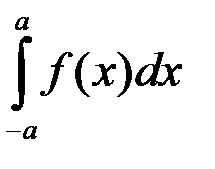 равен:
равен:
1. 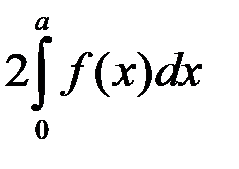 ; +2. 0;
; +2. 0;
3. 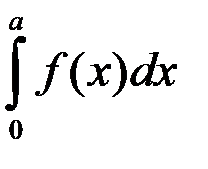 ; 4.
; 4. 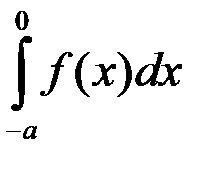 .
.
1))
Функция f (x) является чётной. Тогда интеграл 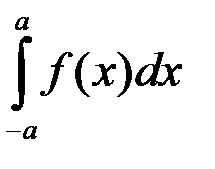 равен:
равен:
1. 0; +2. 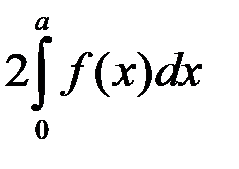 ;
;
3. 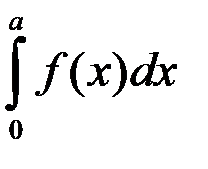 ; 4.
; 4. 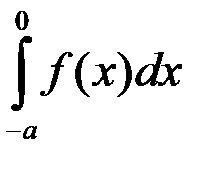 .
.
))
Формула среднего значения для определённого интеграла 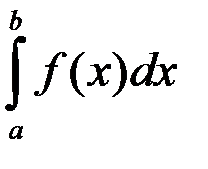 и точки c Î [ a; b ]:
и точки c Î [ a; b ]:
1. 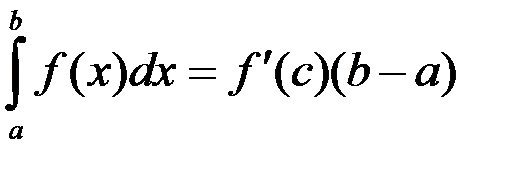 ; 2.
; 2. 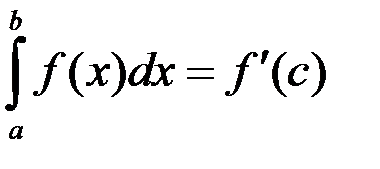 ;
;
+3. 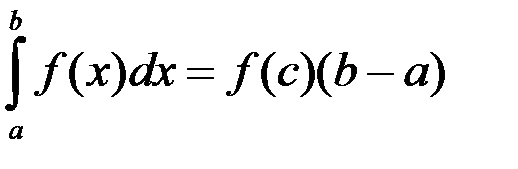 ; 4.
; 4. 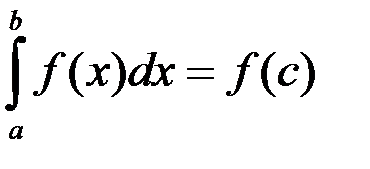 .
.
))
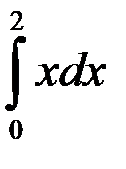 равен:
равен:
1. 4; +2. 3;
3. - 2; 4. - 4.
))
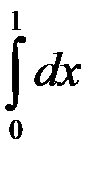 равен:
равен:
1. 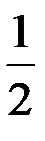 ; +2. 1;
; +2. 1;
3. 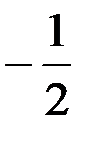 ; 4. - 1.
; 4. - 1.
))
Формула Ньютона-Лейбница: если F(x) – первообразная функции f (x), то 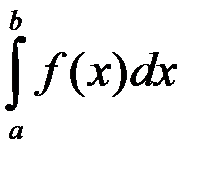 равен:
равен:
1. F(a) – F(b); 2. f (a) – f (b);
3. f (b) – f (a); +4. F(b) – F(a).
))
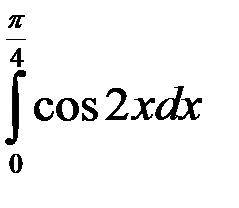 равен:
равен:
1. 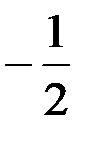 ; +2.
; +2. 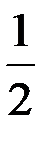 ;
;
3. 1; 4. – 1.
))
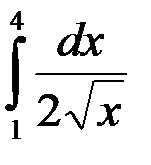 равен:
равен:
1. 2 2. – 1;
+3. 1 4. 0.
))
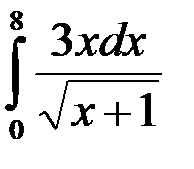 равен:
равен:
|
|
ответ: 40.
))
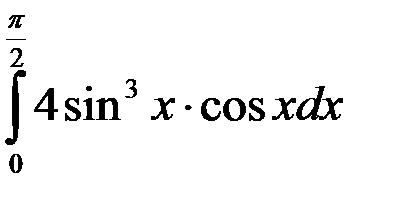 равен:
равен:
|
|
ответ: 1.
))
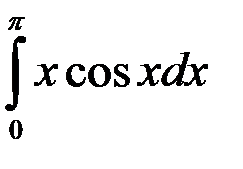 равен:
равен:
|
|
ответ: - 2 .
))
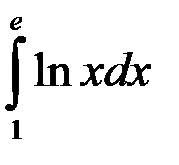 равен:
равен:
|
|
ответ: 1.
))
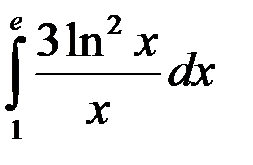 равен:
равен:
|
|
ответ: 1.
)
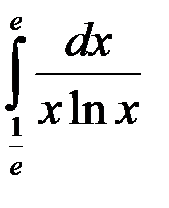 равен:
равен:
|
|
ответ: 0.
))
Площадь, ограниченная линиями y = 12x – 3x2 и y = 0 равна:
|
|
ответ: 32.
)
Площадь, ограниченная линиями 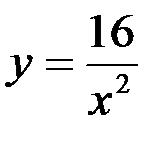 и y = 17 – x2, расположенными в первом квадранте, равна:
и y = 17 – x2, расположенными в первом квадранте, равна:
|
|
ответ: 18.
))
Площадь, ограниченная линиями 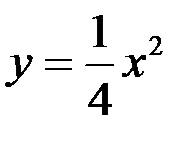 и
и 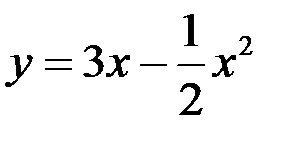 , равна:
, равна:
|
|
ответа: 4.
))
Длина дуги кривой r = 2sinj (0 £ j < p), заданной в полярных координатах 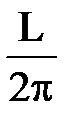 , равна:
, равна:
|
|
ответ: 1
))
Объём тела вращения вокруг Ох криволинейной трапеции, ограниченной линиями у2 = х и у = х2, равен V. Тогда 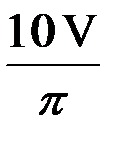 :
:
|
|
ответ: 3.
))
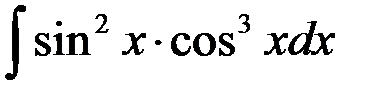
+1. 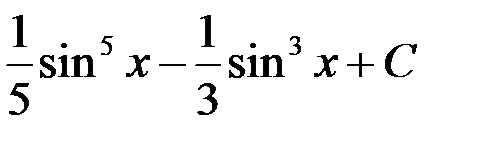 ; 2.
; 2. 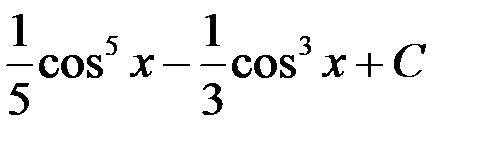 ;
;
3. 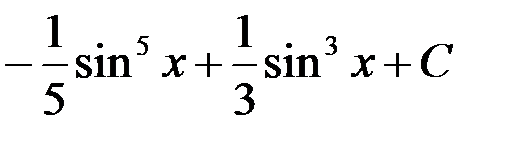 ; 4.
; 4. 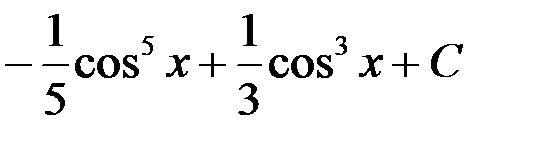 .
.
1))
В оценке определённого интеграла 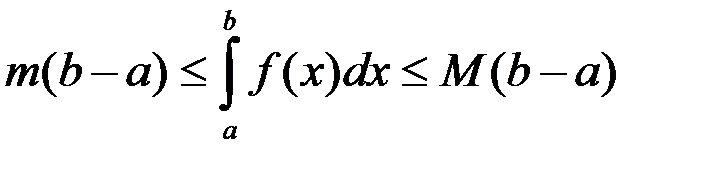 для функции f (x) на отрезке [a; b] выполняется:
для функции f (x) на отрезке [a; b] выполняется:
1. M £ f (x) £ m; +2. m £ f (x) £ M;
3. f (x) = M – m; 4. f (x) = m + M.
))
Функция f (x) – непрерывна на [a; +¥). Тогда 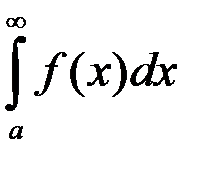 является:
является:
1. неопределённым интегралом; 2. определённым интегралом;
+3. несобственным интегралом I-го рода;
4. несобственным интегралом II-го рода;
))
Несобственный интеграл 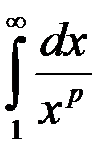 сходится, если:
сходится, если:
1 p = 0; +2. p > 1;
3. p £ 1; 4. p = 1.
))
Несобственный интеграл 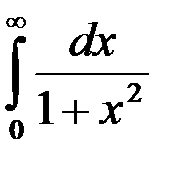 равен:
равен:
1. 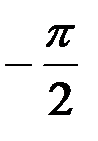 ; 2. 0;
; 2. 0;
+3. 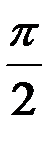 ; 4. 1.
; 4. 1.
))
Несобственный интеграл 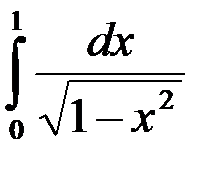 равен:
равен:
1. 0; 2. 1;
+3. 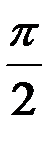 ; 4. - 1.
; 4. - 1.
))
Несобственный интеграл 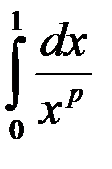 сходится, если:
сходится, если:
1 p > 1; 2. p ³ 1;
3. p = 1; +4. p < 1.








