4. совокупность всех функций f(x) + C, где С – произвольная постоянная.
)
Первообразной для функции f(x) на интервале (a, b) называется функция F(x), если ...
(( V ФАЙЛ))
f ¢ (x) = F(x)
((V ФАЙЛ ))
f ¢ (x) = F ¢ (x)
((V ФАЙЛ +))
F ¢ (x) = f(x)
((V ФАЙЛ ))
f(x) = F(x)
)
Первообразная функция F(x) для функции f(x) = cos x равна ...
((V ФАЙЛ ))
- cos x + C
((V ФАЙЛ ))
- sin x + C
((V ФАЙЛ +))
sin x + C
((V ФАЙЛ ))
cos x + C
)
Первообразная для функции 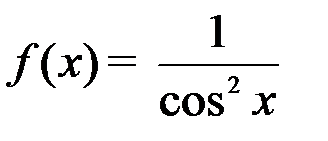 равна ...
равна ...
(( V ФАЙЛ))
arctg x + C
((V ФАЙЛ ))
arcctg x + C
((V ФАЙЛ ))
ctg x + C
(( V ФАЙЛ +))
tg x + C
)
F(x) – одна из первообразных для функции f(x). Тогда любая первообразная F(x) для функции f(x) равна:
1. F(x) = F(x) + f(x); 2. F(x) = f(x);
+3. F(x) = F(x) + C; 4. F(x) = F(x).
)
Первообразная функция F(x) для функции f(x) = x равна:
1. x + C; 2. - x + C; +3. 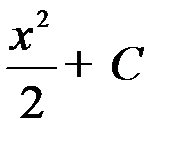 ; 4.
; 4. 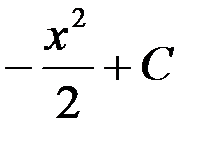 .
.
УС: 1
ВРЕМЯ 1 мин.
)
Соответствие первообразной F(x) функции f(x):
1-я пара: 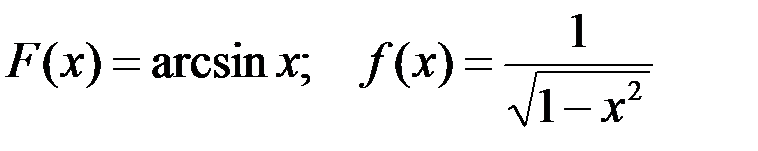 ;
;
2-я пара: 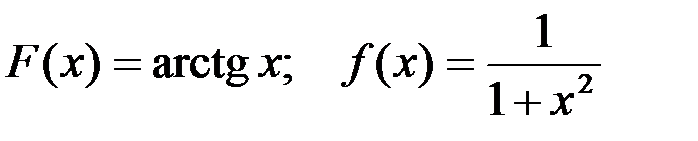 ;
;
3-я пара: 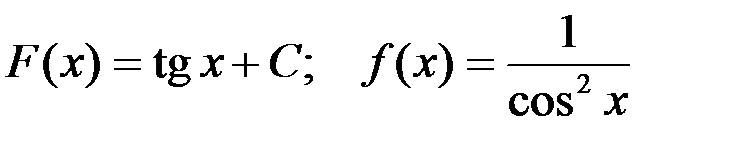 ;
;
4-я пара: 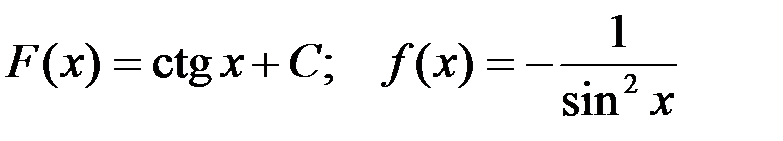 ;
;
5-я пара: 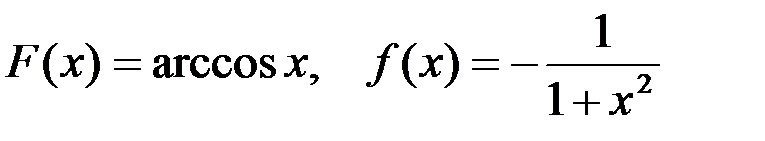 ;
;
6-я пара: 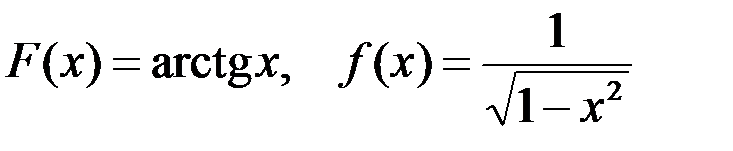
УС: 2
ВРЕМЯ 2 мин.
)
F(x) – первообразная для функции f(x). Тогда неопределённым интегралом 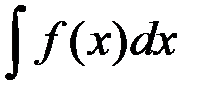 называется
называется
1. сама первообразная F(x);
2. сумма F(x) + f(x);
+3. совокупность всех первообразных F(x) + C;
4. совокупность всех функций f(x) + C, где С – произвольная постоянная.
)
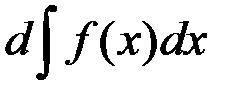 ¾ дифференциал неопределённого интеграла равен:
¾ дифференциал неопределённого интеграла равен:
1. f(x); 2. F(x); +3. f(x)dx; 4. F(x)dx,
где F(x) – первообразная функции f(x).
)
F(x) – первообразная для функции f(x). Тогда 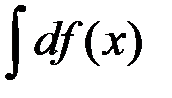 равен:
равен:
1. f(x); 2. F(x); +3 f(x) + C; 4 F(x) + C,
где С – произвольная постоянная.
)
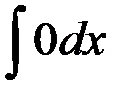 равен:
равен:
1. 0; +2. С; 3. 1; 4. х.
)
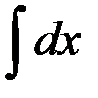 равен:
равен:
1. 1; +2. х + С; 3. х2; 4. х2 + С.
)
Соответствие неопределённых интегралов функциям:
1-я пара: 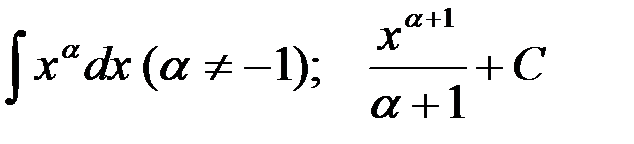 ;
;
2-я пара: 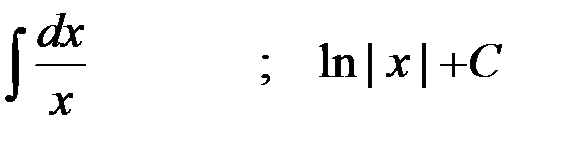 ;
;
3-я пара: 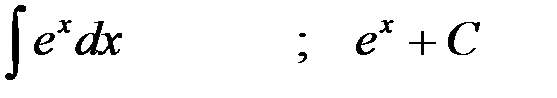 ;
;
4-я пара: 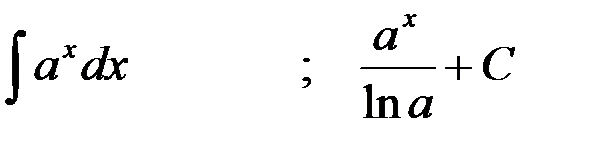 ;
;
5-я пара: 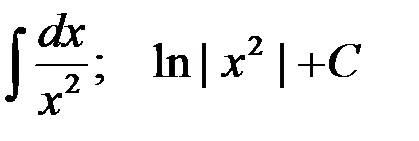 ;
;
6-я пара: 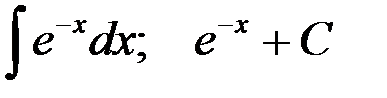 .
.
)
Соответствие функций неопределённым интегралам:
1-я пара: 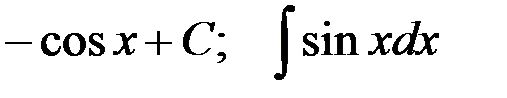 ; 2-я пара:
; 2-я пара: 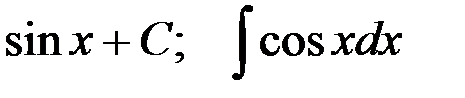 ;
;
3-я пара: 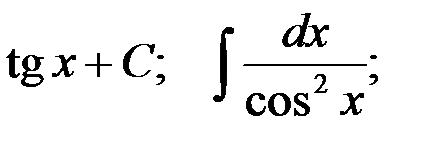 4-я пара:
4-я пара: 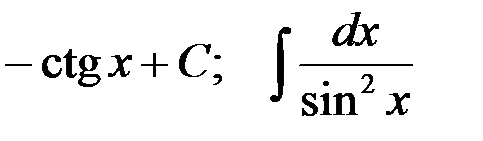 ;
;
5-я пара 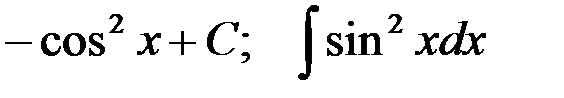 ; 6-я пара
; 6-я пара 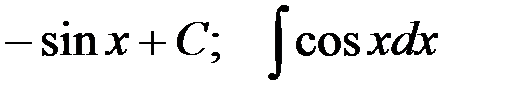 .
.
)
Соответствие функций неопределённым интегралам:
1-я пара: 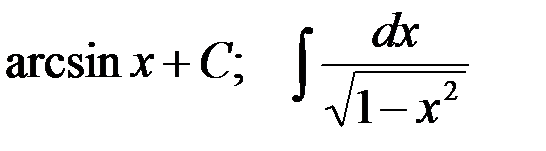 : 2-я пара:
: 2-я пара: 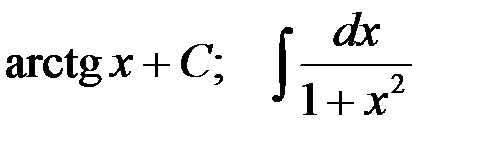 :
:
3-я пара: 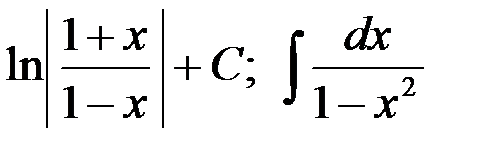 ;
;
4-я пара: 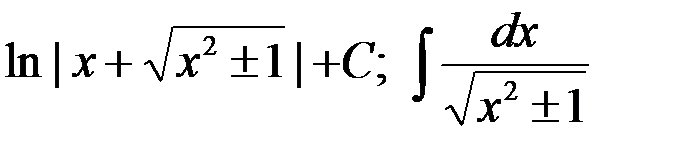 :
:
5-я пара: 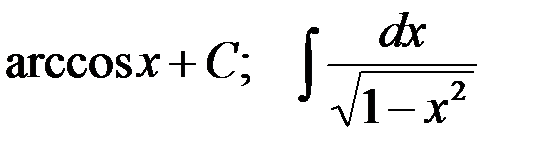 ; 6-я пара:
; 6-я пара: 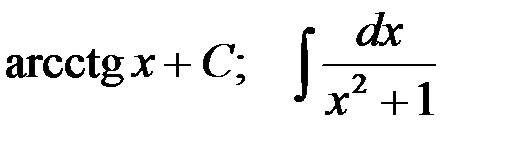 .
.
)
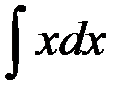 равен:
равен:
1. x + C; 2. 2x2 + C; +3. 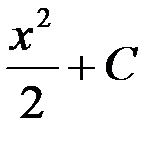 ; 4. 2x + C.
; 4. 2x + C.
)
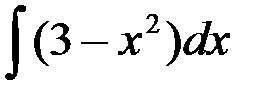 равен:
равен:
1. 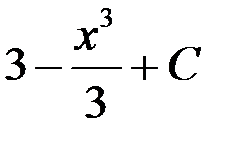 ; 2.
; 2. 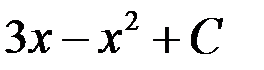 ;
;
+3. 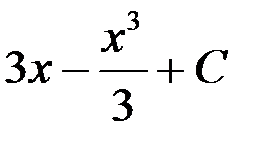 ; 4.
; 4. 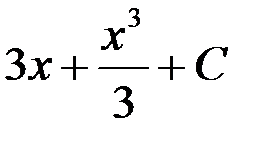 .
.
)
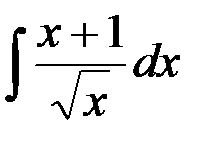 равен:
равен:
1. 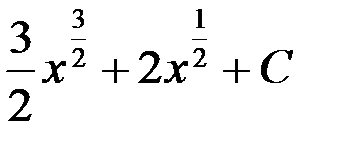 ; +2.
; +2. 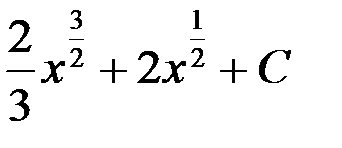 ;
;
3. 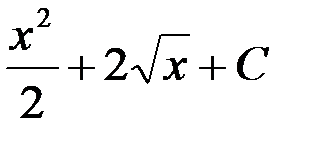 ; 4.
; 4. 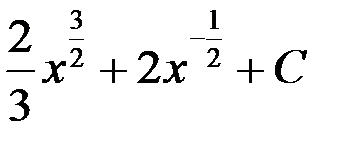 .
.
)
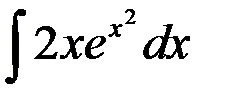 сводится к табличному заменой:
сводится к табличному заменой:
1. x = t; 2. 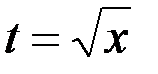 ; +3. t = x2; 4.
; +3. t = x2; 4. 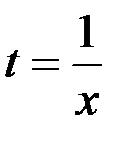
)
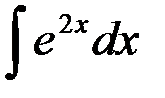 равен:
равен:
1. e2x + C; 2. 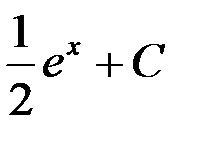 ; +3.
; +3. 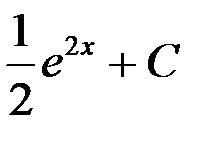 ; 4. 2e2x + C.
; 4. 2e2x + C.
)
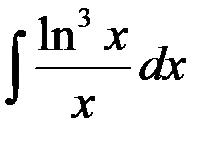 сводится к табличному заменой:
сводится к табличному заменой:
+1. t = lnx; 2. 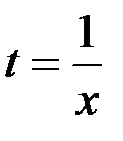 ; 3. t = ln3x; 4. t = x.
; 3. t = ln3x; 4. t = x.
)
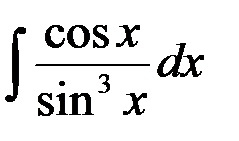 равен:
равен:
+1. 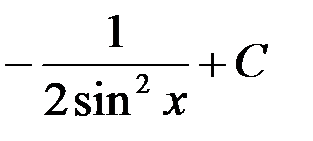 ; 2.
; 2. 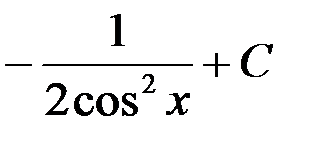 ;
;
3. 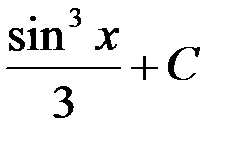 ; 4.
; 4. 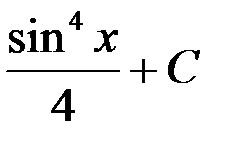 .
.
((Q ВЫБОР 1))
3.4.1.6/5
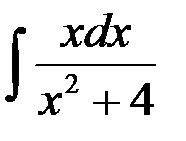 равен:
равен:
1. 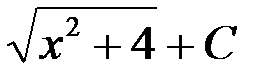 ; 2. (x2 + 4) + C;
; 2. (x2 + 4) + C;
3. ln(x2 + 4) + C; +4. 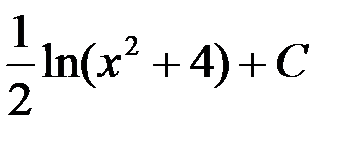 .
.
)
Соответствие функций неопределённым интегралам:
1-я пара: 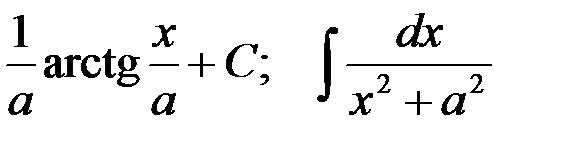 ;
;
2-я пара: 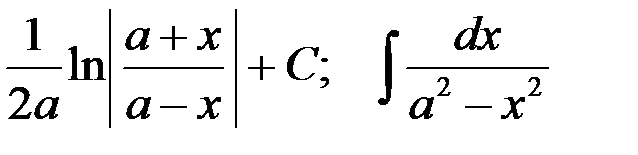 ;
;
3-я пара: 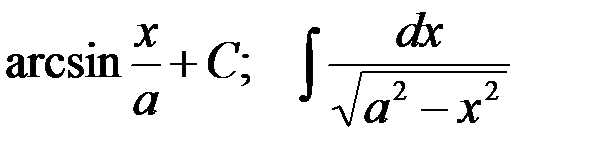 ;
;
4-я пара: 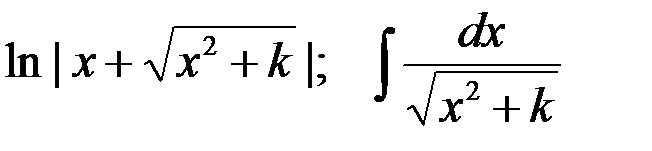 ;
;
5-я пара: 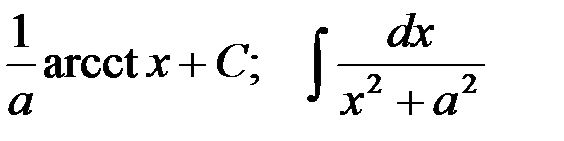 ;
;
6-я пара 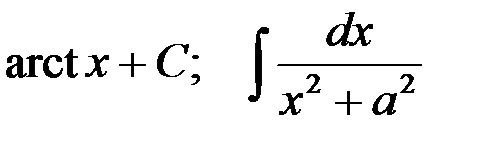 .
.
)
Формула интегрирования по частям. òud v равен
+1. u v - òv du; 2. u - òv du; +3 v u - òv du; 4 v - òud v.
УС: 1
ВРЕМЯ 1 мин.
)
Применить формулу интегрирования по частям в интеграле òx2lnxdx при u =
1. x2; 2. x; 3. xlnx; +4. lnx.
)
Применить формулу интегрирования по частям в интеграле òx2cos 2xdx при u =
1. cos2x; +2. x2; 3. xcos2x; 4. x.
)
òxe-x dx равен:
1. 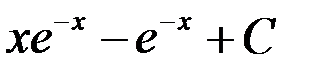 ; +2.
; +2. 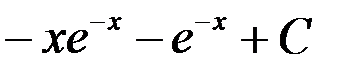 ;
;
3. 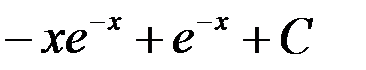 ; 4.
; 4. 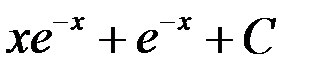 .
.
)
òarctgxdx равен:
1. 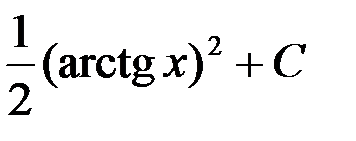 ; +2.
; +2. 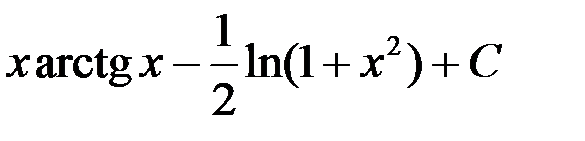 ;
;
3. 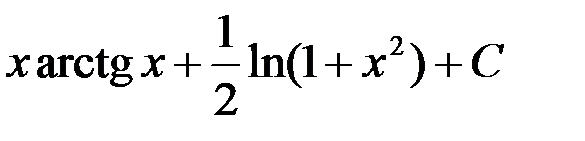 ; 4.
; 4. 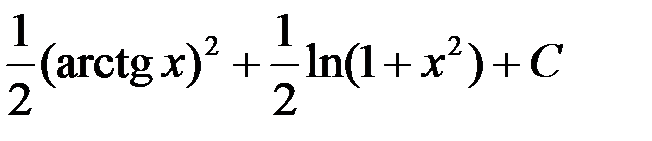 .
.
ответ: 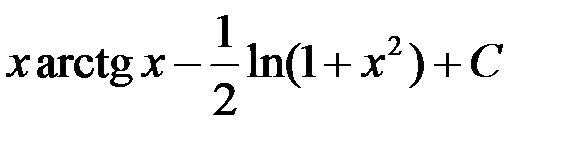
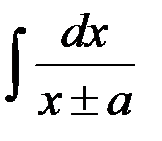 равен:
равен:
1. (x ± a) + C; 2. 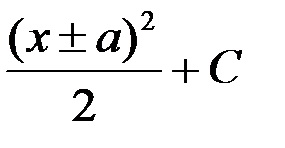 ;
;
+3. ln| x ± a | + C; 4. 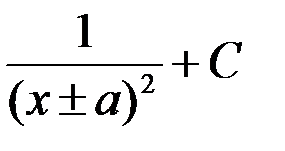 .
.
)
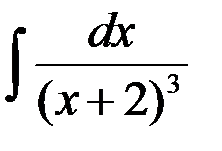 равен:
равен:
1. (x + 2)3 + C; +2. 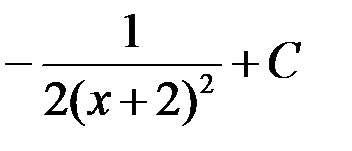 ;
;
3. 2(x + 2)2 + C; 4. 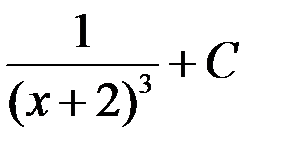 .
.
)
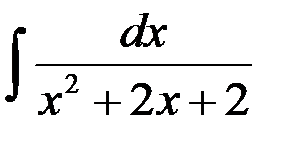 равен:
равен:
+1. arctg(x + 1) + C; 2. 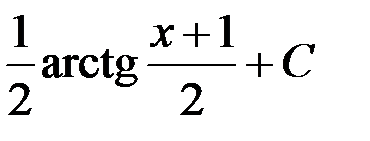
3. 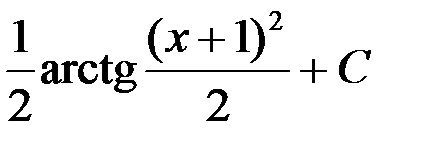 ; 4.
; 4. 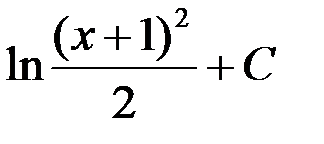 .
.
)
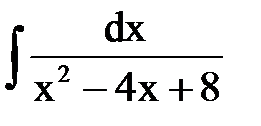 равен:
равен:
1. 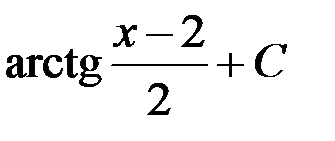 ; +2.
; +2. 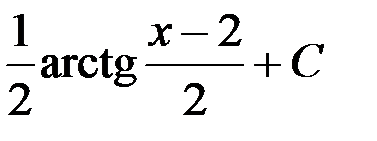 ;
;
3. 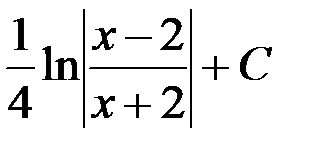 ; 4.
; 4. 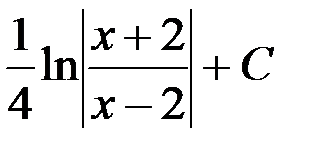 .
.
((
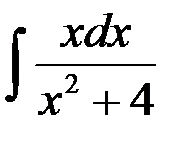 равен:
равен:
1. ln(x2 + 4) + C; 2. 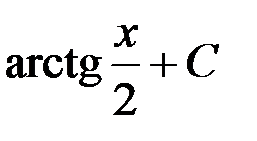 ;
;
+3. 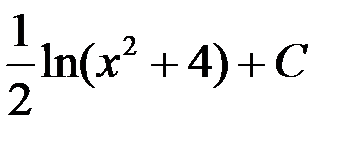 ; 4.
; 4. 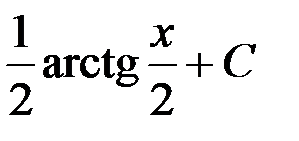 .
.
))
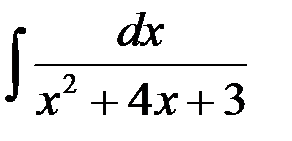 равен:
равен:
1. arctg(x + 2) + C; 2. 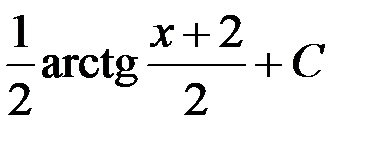 ;
;
+3. 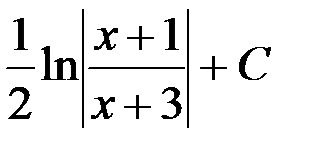 ; 4.
; 4. 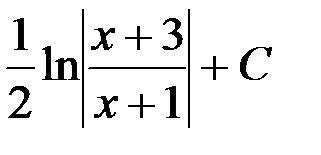 .
.
))
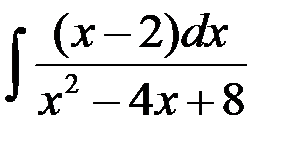 равен:
равен:
1. ln| x2 - 4x + 8 | + C; +2. 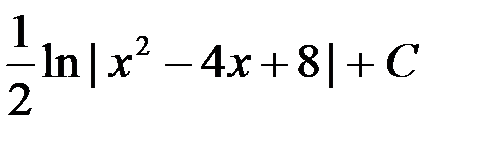 ;
;
3. 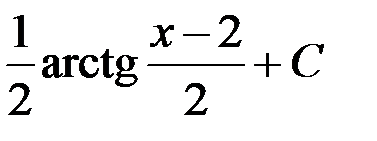 ; 4.
; 4. 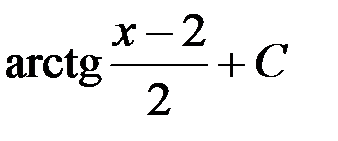 .
.
))
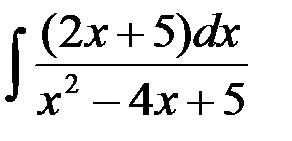 равен:
равен:
1. ln| x2 - 4x + 5 | + C; 2. ln| x2 - 4x + 5 | 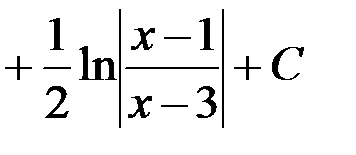 ;
;
+3. ln| x2 - 4x + 5 | + 9arctg (x - 2) + C; 4. arctg (x - 2) + C.
))
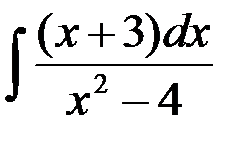 равен:
равен:
1. ln | x2 + 4 | + C; +2. 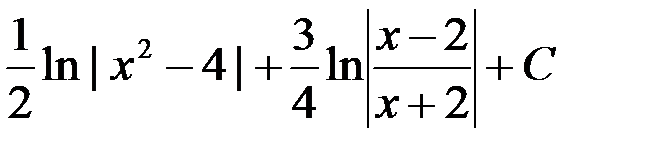 ;
;
3. 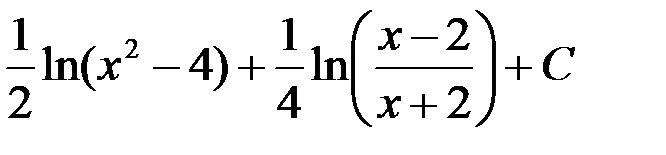 ; 4.
; 4. 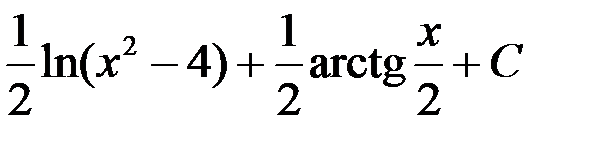 .
.
))
Рациональная дробь (рациональная функции) 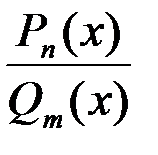 (Pn(x), Qm(x) – многочлены степени n и m) является правильной, если:
(Pn(x), Qm(x) – многочлены степени n и m) является правильной, если:
1. n £ m; 2. n > m; +3. n < m; 4. n = m.
)
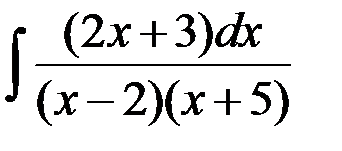 равен:
равен:
1. ln | x - 2 | - ln | x + 5 | + C; +2. ln |( x - 2)( x + 5)| + C;
3. ln | x + 5 | - ln | x - 2 | + C; 4. 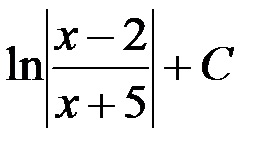 .
.
1))
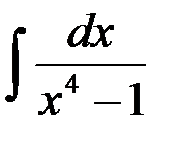 равен:
равен:
+1. 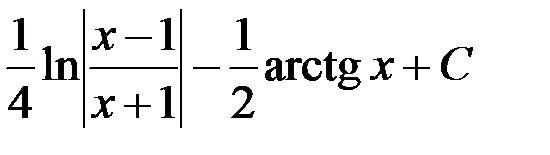 ; 2.
; 2. 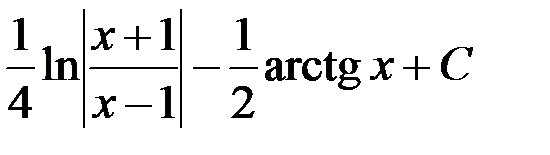 ;
;
3. 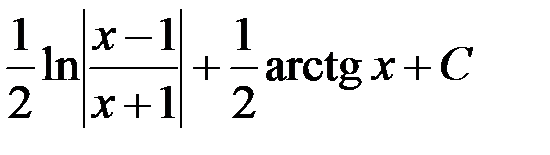 ; 4.
; 4. 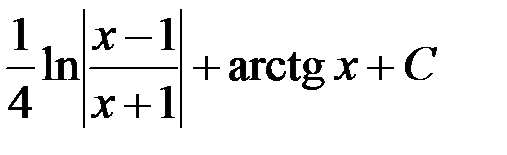 .
.
1))
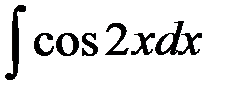 равен:
равен:
1. sin 2x + C; +2. 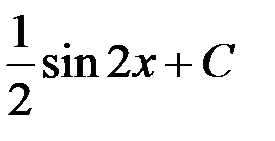 ;
;
2. 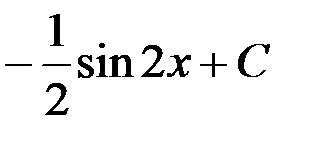 ; 4. - sin 2x + C.
; 4. - sin 2x + C.
УС: 2
ВРЕМЯ 1 мин.
((
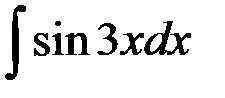 равен:
равен:
1. cos 3x + C; 2. 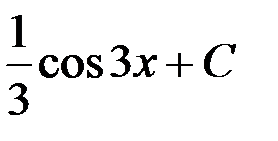 ;
;
3. - cos 3x + C; +4. 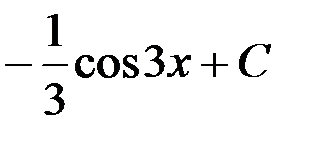 .
.
))
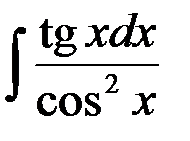 равен:
равен:
1. ctg x + C; 2. - ctg x + C;
3. tg2x + C; +4. 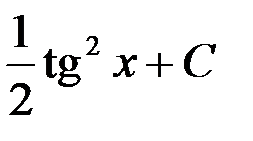 .
.
))
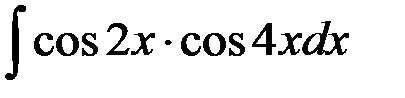 равен:
равен:
1. 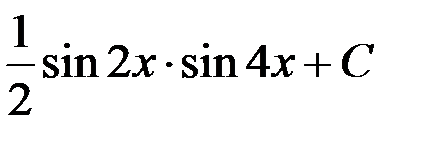 ; 2.
; 2. 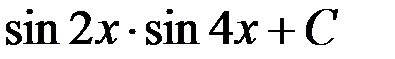 ;
;
+3. 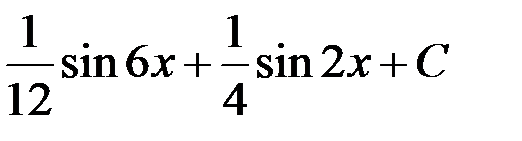 ; 4.
; 4. 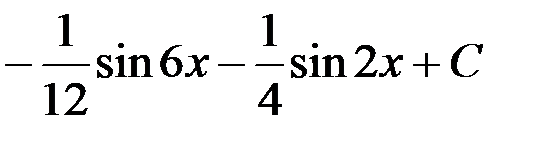 .
.
))
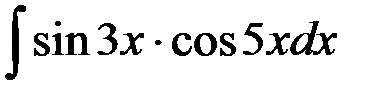 равен:
равен:
1. 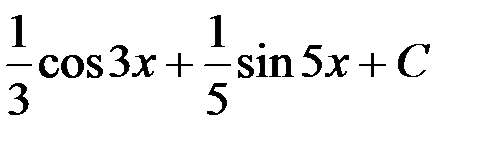 ; 2.
; 2. 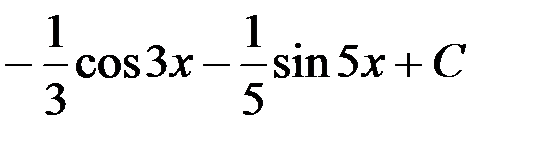 ;
;
3. 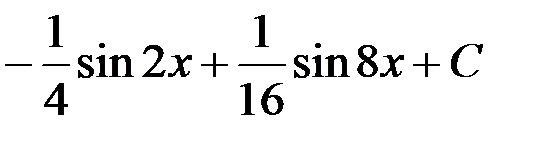 ; +4.
; +4. 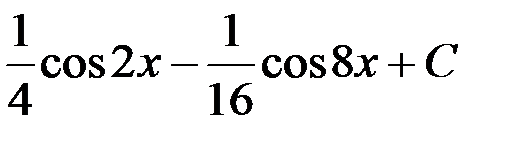 .
.
))
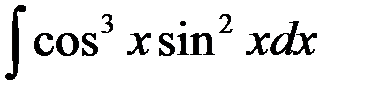 равен:
равен:
1. 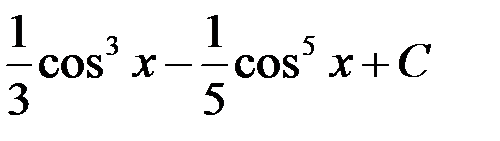 ; 2.
; 2. 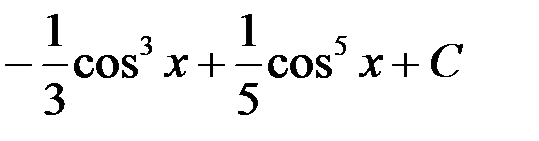 ;
;
+3. 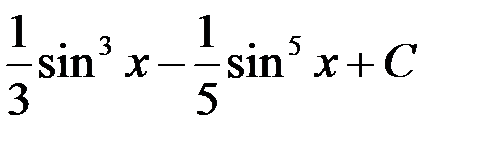 ; 4.
; 4. 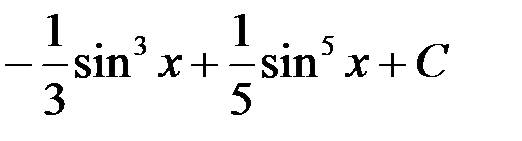 .
.
))
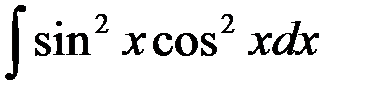 равен:
равен:
1. 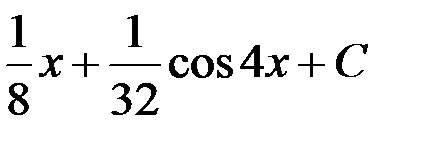 ; 2.
; 2. 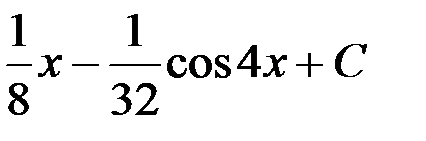 ;
;
+3. 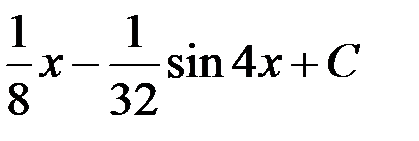 ; 4.
; 4. 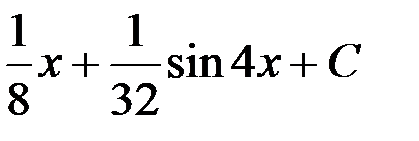 .
.
))
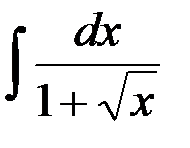 равен:
равен:
1. 2(x - ln (x + 1)) + C; +2. 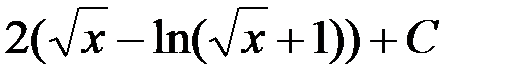 ;
;
3. 2(x - ln (x + 1)) + C; 4. 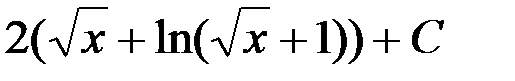 .
.
))9
В интеграле 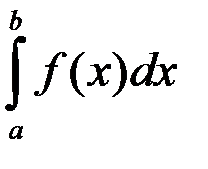 соответствуют определению:
соответствуют определению:
1-я пара: а; нижний предел интегрирования;
2-я пара: b; верхний предел интегрирования;








