Регулятор питания импульсного типа, макета парового котла де-10.
Представлены результаты разработки схемы регулятора питания импульсного типа, макета парового котла и проведены его лабораторные испытания. Задача решена в виде разработки ударного узла импульсного типа. Приведены результаты эксперементов на различных длинах труб, также показана зависимость расхода от частоты ударов клапана. Эффективность разработки заключается, в возможности регулирования расхода импульсным режимом течения жидкости, и использование избыточного располагаемого давления.
Ключевые слова: импульсный режим течения жидкости, регулятор питания макета парового котла, гидротаран, ударный узел, форма кулачка, расход, период вращения.
Объектом исследования является импульсный режим течения жидкости и его применение на макете парового котла ДЕ-10, а также разработка регулятора питания макета парового котла, импульсного типа и разработка схемы установки.
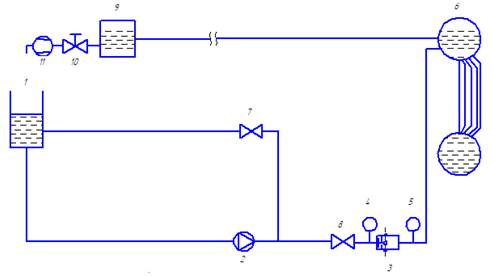
Рисунок 1– Принципиальная схема эксперементальной установки:
1 – ёмкость, 2 – циркуляционный насос, 3 – регулирующий клапан (ударный узел), 4,5 – манометр, 6 – макет парового котла ДЕ – 10, 7,8 – задвижка, 9 – емкость для измерения расхода, 10 – кран, 11 – водомер.
Главным фактором, влияющим на работу ударного клапана, нашей установки является - форма кулачкового механизма, это один из важнейших подвижных элементов клапана, далее рассмотрим 2 формы кулачка и их развёртки, показывающие время его открытия и закрытия. Первым будет показан кулачок элипсоидной формы:
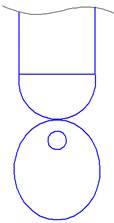
Рисунок 2 – Элипсоидная форма кулачка
И соответственно его полученная развертка:
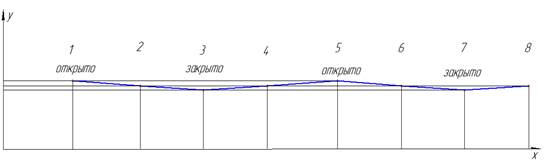
Рисунок 3 – Развертка элипсоидной формы кулачка
Теперь возьмем нестандартный кулачок, у которого отсутствует часть поверхности, ее видно на рисунке, для того чтобы увеличить его характеристики. Это проверим разверткой периметра. Впоследствии, сравним полученные развертки стандартной и нестандартной формы кулачка, с усеченной частью.
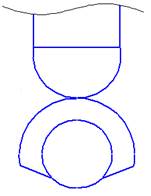
Рисунок 4 – Нестандартная форма кулачка
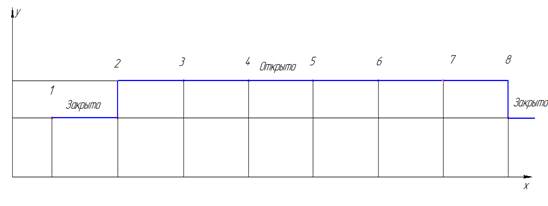
Рисунок 5 – Развертка нестандартного кулачка
Сравнивая полученные развертки, видим что, элипсоидной формы кулачка более прямолинейная, практически прямая. Это говорит, о том что, у такой формы кулачка нет явного момента открытия и закрытия, получается, что он всегда либо полуоткрыт, либо полузакрыт. Соответственно – это влияет на характер подачи жидкости, его можно назвать почти импульсным.
Теперь рассмотрим нестандартную форму кулачка, на ее развертке мы можем видеть характерные изгибы графика, которые показывают момент открытия и закрытия клапана. Можно сказать, нестандартная форма более эффективна, чем стандартная форма.
Развертка кулачка в идеальном случае должна соответствовать периодам открытого и закрытого положения ударного клапана гидротарана. Это значит, что колебания происходят с той же частотой, что и колебания жидкости в трубопроводе, что является оптимальным для импульсных систем.
Поэтому использование элипсоидной формы кулачка является нерациональным, потому что, характеристики расхода в секунду будут совпадать, независимо от того, как мы будем изменять частоту вращения кулачка.
От формы кулачка напрямую зависит расход, и соответственно время полного цикла, также свои коррективы вносит коэффициент разгона, от зависимости которого, меняется время цикла (полного оборота кулачка).
Таблица 1 – Зависимость продолжительности цикла от коэффициента разгона
| Значение коэффициента разгона k . | Продолжительность цикла T,сек |
| 0,05 | 0,237199 |
| 0,10 | 0,415151 |
| 0,15 | 0,594313 |
| 0,20 | 0,775335 |
| 0,25 | 0,958928 |
| 0,30 | 1,145893 |
| 0,35 | 1,337153 |
| 0,40 | 1,533805 |
| 0,45 | 1,737183 |
| 0,50 | 1,948962 |
| 0,55 | 2,171304 |
| 0,60 | 2,407095 |
| 0,65 | 2,660343 |
Продолжение таблицы 1
| 0,70 | 2,936871 |
| 0,75 | 3,245666 |
| 0,80 | 3,601737 |
| 0,85 | 4,033163 |
| 0,90 | 4,602912 |
| 0,95 | 5,511804 |
И полученную зависимость отразим на рисунке 6.
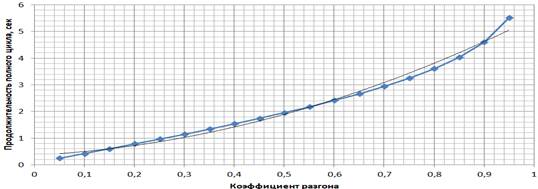
Рисунок 6 – Зависимость продолжительности цикла от коэффициента разгона
Поэтому делаем вывод, что коэффициент разгона и является главным фактором, влияющим на продолжительность полного цикла работы импульсной установки. Хочется уточнить, что чем ближе значение коэффициента разгона к единице, тем дольше длится продолжительность цикла.
Для того, чтобы провести эксперимент нам нужно знать: объем начального и конечного количества жидкости, время работы установки, число ударов кулачка внутри клапана.
Чтобы узнать расход и пропускную способность данной установки, вычислим начальный объем жидкости. Нам известно, что 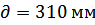 . Из этого узнаем площадь сечения:
. Из этого узнаем площадь сечения:
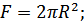
| (36) |
Переведем мм в дм, для того, чтобы в дальнейшем было проще узнать объем жидкости.
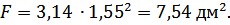
|
тогда начальный объем жидкости:
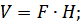
|
высота столба жидкости H=50см, соответственно 5 дм.
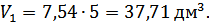
|
После проведения эксперимента, уровень столба жидкости упал на 0,7 дм, соответственно делаем повторный расчет, чтобы узнать количество жидкости, которое вытекло за время эксперемента, а это 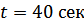 .
.
Объем после проведения эксперемента:
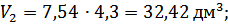
|
Найдя разницу, между начальным и конечным объемом жидкости найдем, количество воды вытекшей через нашу установку:
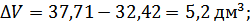
|
Соответственно получаем, что во время эксперемента у нас ушло 5,2 литров воды. Зная это, вычислим количество жидкости, проходящей за 1 секунду:
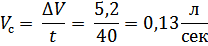
|
Выходит, что в секунду установка пропускает через себя 130 грамм воды.
И так мы проделываем много раз, чтобы получить зависимость числа оборотов кулачка от проталкиваемой им жидкости, на суммарном расстоянии труб 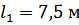 .
.
Соответственно проделываем этот эксперимент при длине трубы 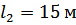 .Для определения оптимальной длины трубопровода.
.Для определения оптимальной длины трубопровода.
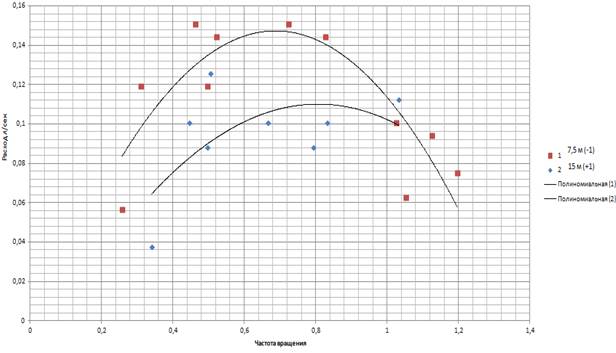
Рисунок 7 – Расход через ударный клапан в зависимости от частоты вращения
Сделаем вывод: Исходя, из полученных данных мы видим, что при длине трубы в 7,5 метров получается самое оптимальное соотношение длины трубопровода и расхода. Также можно отметить, при высоких оборотах не сильно меняется количество выходящей жидкости, это видно по данным таблицы. При длине трубы в 15 метров, мы видим снижение характеристик расхода и соответственно зависимость расхода от частоты вращения кулачка, чем она выше, тем ниже конечный расход, и наоборот чем ниже частота вращения, тем выше расход.








