Чистый изгиб имеет место, если в сечении возникает только изгибающий момент (рис. 1.1, а), поперечный изгиб – если одновременно с моментом возникает поперечная сила (рис. 1.1, б).
Виды опор балок
Прямолинейный брус, работающий на изгиб, называют балкой. Изгиб вызывают силы, перпендикулярные продольной оси z, или пары сил, лежащие в плоскостях, проходящих через ось z (1.1, a). Сама ось z , прямолинейная до деформации, при изгибе становится кривой линией. При этом волокна, расположенные в выпуклой части изогнутой балки, растягиваются, а в вогнутой – сжимаются.
Рассмотрим балки, поперечные сечения которых имеют вертикальную ось симметрии. Для того чтобы балка воспринимала нагрузку и передавала ее на другие части конструкции или на основание, она должна иметь опорные устройства. В зависимости от способа крепления различают три основных типа балок (рис. 1.2, а-в):
1. Двухопорная балка (одна опора - шарнирно-неподвижная, другая – шарнирно – подвижная; расстояние между опорами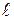 
называется пролетом балки).
2. Консоль (один конец жестко защемлен; длина балки a – вылет консоли).
3. Консольная балка (балка, свободно лежащая на двух опорах со свешивающимися концами – консолями).
Балки составляют большую долю элементов конструкций – это балки перекрытий, пролетные строения кранов, валы и оси механизмов, крыло самолета и т.д.
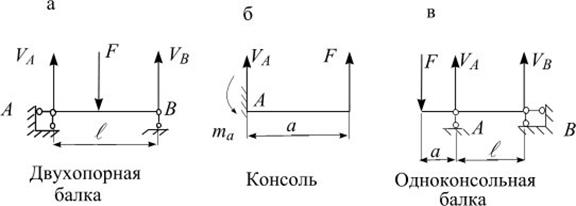
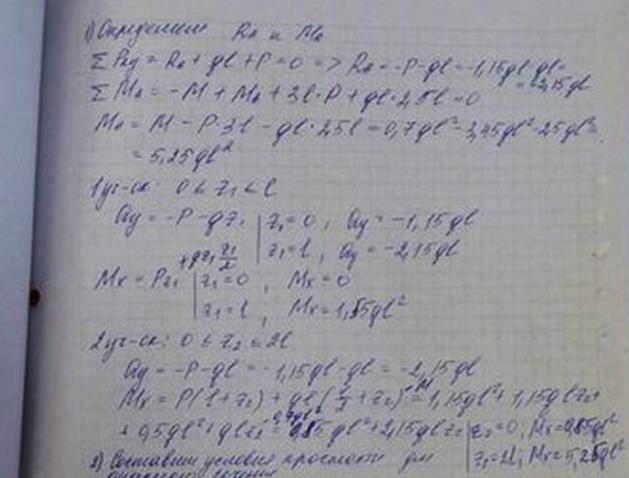
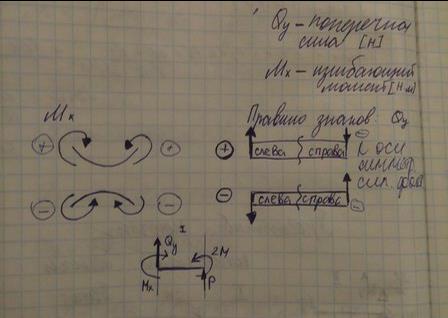
18. Внутренние усилия, правило знаков для поперечной силы и изгибающего момента. Построение эпюр поперечных сил и изгибающих моментов. Эпюры поперечных сил и изгибающих моментов в простых балках.
Под действием внешних сил тело деформируется. При этом возникают дополнительные внутренние силы, которые отражают сопротивление материала деформированию и разрушению.
N – продольная (нормальная) сила;
, 
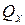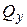– поперечные силы вдоль осей х и у;
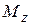– крутящий момент;
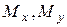– изгибающие моменты относительно осей х и у.
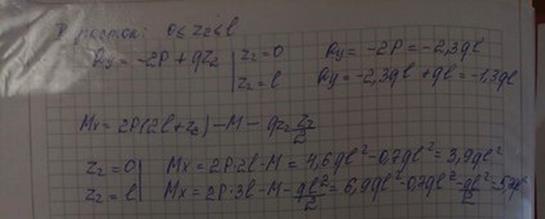
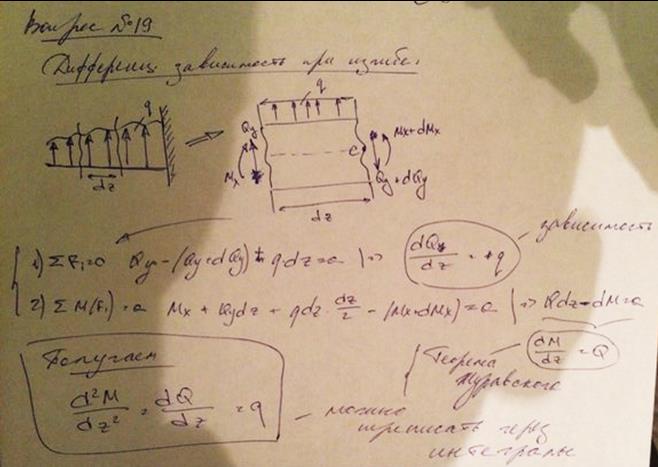
19. Дифференциальные зависимости при изгибе, их следствия и использование для контроля правильности построения эпюр внутренних усилий.
20. Условие прочности балок при изгибе по нормальным напряжениям.
Условие прочности по нормальным напряжениям
,
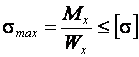где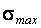 
– наибольшее по модулю напряжение в поперечном сечении; 
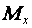– изгибающий момент; wx – осевой момент сопротивления; 
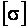– допускаемые нормальные напряжения.
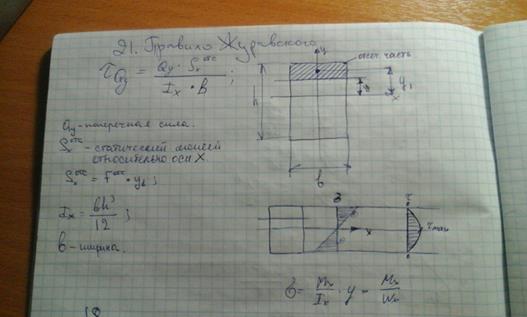
21. Формула Д.И. Журавского для определения касательных напряжений при изгибе на примере прямоугольного сечения.
