По формуле (7) определяются касательные напряжения в любой точке поперечного сечения вала.
По закону парности такие же касательные напряжения возникают в продольных сечениях (рис. 1.5, а), и прямоугольный элемент испытывает состояние чистого сдвига (рис. 1.5, б).
Анализ формулы (7) показывает:
1. Касательные напряжения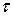 
распределены вдоль радиуса по линейному закону (рис. 4.19);
2. В каждой точке напряжения 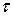перпендикулярны текущему радиусу;
3. 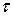= 0 в центре круга ( 
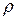= 0);
4. Максимальные напряжения возникают в крайних точках сечения:
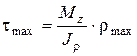, (8)
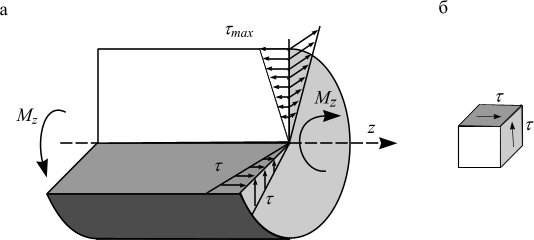
Рисунок 1.5
или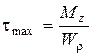 
, (9)
где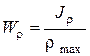 
– геометрическая характеристика сечения, называемая полярным моментом сопротивления, см3 или м3.
Определение углов закручивания.
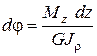, (10)
где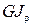 
– жесткость сечения при кручении.
После интегрирования (10) получим взаимный угол закручивания двух сечений, расположенных на расстоянии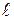 
.
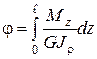. (11)
Если на участке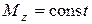 
и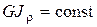 
, то после интегрирования получаем в радианах:
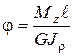. (12)
Полный угол закручивания вала определяется суммированием по участкам. Для оценки жесткости вала используют относительный угол закручивания (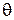 
), который является мерой деформации при кручении.
Из (10) получаем:
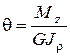. (13)
Эпюры касательных напряжений
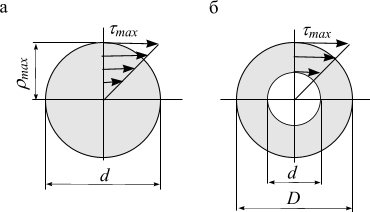
Рисунок 1.6
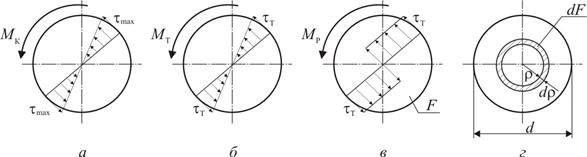
Рисунок 1.7 - Эпюры касательных напряжений
16. Понятие о чистом сдвиге. Напряжения в поперечных сечениях.
Сдвиг – случай нагружения, при котором в поперечном сечении возникает только поперечная сила Q :
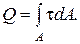(1)
A – площадь (здесь писать А)
На границах бесконечно малого прмоугольного элемента возникает только касательное напряжение, то данное напряженное состояние называется чистым сдвигом.
Для всех точек пластины касательные напряжения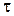 
будут равны
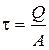, (2)
где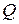 
– сдвигающая сила; 
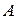– площадь сечения пластины; а касательные напряжения 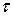принимаем равномерно распределенными по сечению.
Посмотрим, как при чистом сдвиге изменяются напряжения в зависимости от ориентации секущих площадок. Выделим трехгранную призму DCB (рис. 1.1) и рассмотрим ее в равновесии (рис. 1.2).
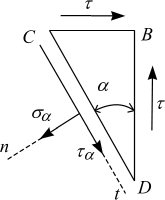
На грани DС возникают как касательные, так и нормальные напряжения. Проецируем все силы, действующие на элемент, на оси n и t.
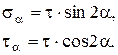(3)
При 
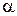= 0 и 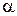= 900 напряжения 
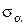= 0,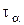 
=t. При 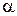= ± 450 напряжения 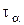= 0, 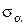= ± t. Следовательно, на гранях элемента, повернутого на 450, будут обнаружены только нормальные напряжения, причем на одной паре граней они растягивающие, на другой – сжимающие (рис. 1.3).
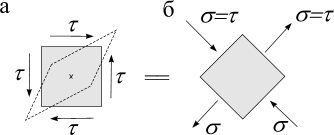
Чистый сдвиг может быть представлен как одновременное растяжение и сжатие по двум взаимно перпендикулярным направлениям.
Закон Гука при чистом сдвиге
Рассмотрим деформации прямоугольного элемента закрепленного с одной стороны
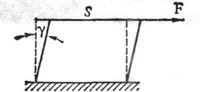
Малый угол, на который изменится первоначальный прямой угол называется углом сдвига или относительным сдвигом величины.
Деформация сдвига характеризуется изменением углов, длин.
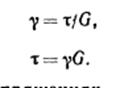Закон Гука (связь между касательным напряжением и углом сдвига)
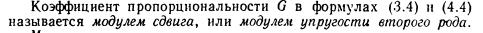
17. Определения прямого и косого изгиба. Плоский изгиб. Чистый и поперечный изгиб. Виды опор балок и вычисление опорных реакций.
Изгиб – такой вид нагружения, при котором в поперечном сечении элемента конструкции возникают поперечная сила и изгибающий момент.
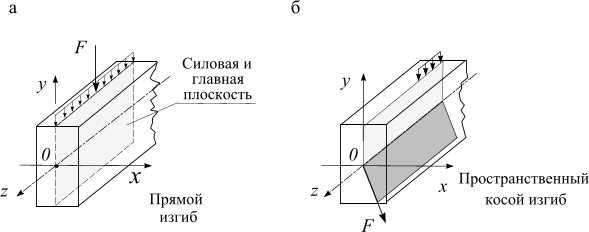
Различают косой и прямой изгиб.
Прямой изгиб балки возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.
Плоский изгиб – изгиб, при котором все усилия, изгибающие балку, лежат в одной из плоскостей симметрии балки (в одной из главных плоскостей).