Кручение – вид нагружения бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент, обозначаемый или .
Деформация кручения возникает при нагружении бруса парами сил, плоскости действия которых перпендикулярны его продольной оси. Моменты этих пар будем называть скручивающими моментами и обозначать m (рис. 1.1).
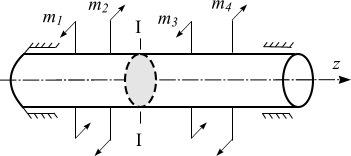
Рисунок 1.1
Брус, работающий на кручение, называется валом.
Вычисление крутящих моментов. Построение эпюр
При расчете вала внешние скручивающие моменты могут быть выражены через мощность и угловую скорость.
m = P / (Н/м)
m =9,55 P / n n -число оборотов
Если вал находится в состоянии покоя или равномерного вращения то алгебраическая сумма всех скучивающих моментов равна 0.
Крутящий момент, возникающий в произвольном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к отставной части
Мк= 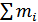
/
/ 

15. Кручение круглого вала: касательные напряжения и относительный угол закручивания. Эпюры напряжений по высоте сечений. Потенциальная энергия деформации круглого стержня при кручении.
Представление о характере деформации кручения можно получить, подвергая скручиванию модель бруса с нанесенной на его поверхность сеткой продольных и поперечных линий.
После закручивания продольные линии превращаются в винтовые (рис. 1.1). Поперечные линии не искривляются, и расстояние между ними не меняется. Прямоугольники, образованные сеткой, перекашиваются за счет изменения первоначально прямого угла на малый угол  .
.
Брус радиусом 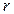 (рис. 1.2) скручивается моментом
(рис. 1.2) скручивается моментом 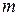 . Образующая
. Образующая 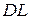 после кручения перейдет в положение
после кручения перейдет в положение 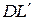 . Сечение I–I повернется на угол
. Сечение I–I повернется на угол 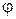 , а сечение II–II на угол
, а сечение II–II на угол 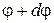 . Следовательно, сечение II–II по отношению к I–I повернется на угол
. Следовательно, сечение II–II по отношению к I–I повернется на угол 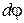 .
.

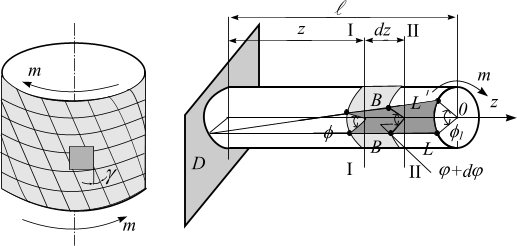
Рисунок 1.1 Рисунок 1.2
В результате наблюдений приходим к следующим гипотезам, на которых основана теория круглых валов:
1. Сечения, плоские до закручивания, остаются плоскими и после закручивания (гипотеза Бернулли);
2. Все радиусы данного сечения остаются прямыми и поворачиваются на один и тот же угол 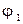 (рис. 4.16), т.е. каждое сечение поворачивается вокруг оси z как жесткий тонкий диск;
(рис. 4.16), т.е. каждое сечение поворачивается вокруг оси z как жесткий тонкий диск;
3. Расстояния между сечениями не меняются, значит, продольные волокна не удлиняются и не укорачиваются, т.е. длина вала 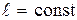 .
.
На основании принятых гипотез кручение круглого бруса можно представить как результат сдвигов, вызванных взаимным поворотом сечений друг относительно друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения. Для их определения рассмотрим три стороны задачи.
Статическая сторона задачи выражается интегральным уравнением равновесия:
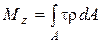 , (1)
, (1)
т.е. крутящий момент 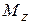 представляет собой результирующий момент внутренних касательных сил
представляет собой результирующий момент внутренних касательных сил 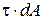 , действующих на бесконечно малых площадках сечения (рис. 4.17):
, действующих на бесконечно малых площадках сечения (рис. 4.17): 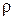 – плечо элементарной силы относительно продольной оси точки О.
– плечо элементарной силы относительно продольной оси точки О.
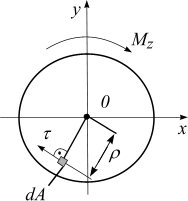
Рисунок 1.3
Рассмотрим геометрическую сторону задачи.
Выделим из бруса элемент 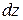 (рис. 1.2) и рассмотрим картину деформирования, приняв левое сечение условно неподвижным (рис. 1.4).
(рис. 1.2) и рассмотрим картину деформирования, приняв левое сечение условно неподвижным (рис. 1.4).
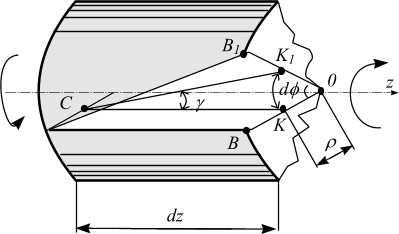
Рисунок 1.4
Радиус ОВ вместе с сечением поворачивается на угол 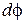 , а образующая CK произвольной точки K переходит в положение СК1, поворачиваясь на угол
, а образующая CK произвольной точки K переходит в положение СК1, поворачиваясь на угол  .
.
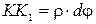 ,
,
а из треугольника СКК1 отрезок 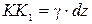 .
.
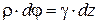 получим выражение угла сдвига на поверхности скручивания элемента, т.е. геометрическое уравнение,
получим выражение угла сдвига на поверхности скручивания элемента, т.е. геометрическое уравнение,
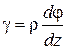 . (2)
. (2)
Потенциальная энергия при кручении
Для определения характеристик прочности и изучения характера разрушения проводят испытания на кручение образцов из различных материалов.
Для пластичных материалов диаграмма кручения подобна диаграмме растяжения. Работа, затрачиваемая на кручение в пределах упругих деформаций, равна количеству потенциальной энергии, накопленной в брусе, и вычисляется как площадь треугольника на диаграмме кручения.
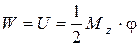 .
.
С учетом (12) имеем:
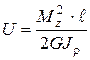 . (14)
. (14)
Физическая сторона задачи определится законом Гука при сдвиге:
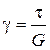 или
или 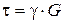 . (3)
. (3)
Проведем синтез трех сторон задачи.
Формула (3) с учетом (2) принимает вид
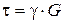
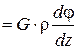 . (4)
. (4)
Подставляя (4) в (1), имеем:
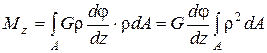 , (5)
, (5)
где интеграл 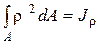 - полярный момент инерции сечения.
- полярный момент инерции сечения.
Из (5) следует:
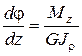 . (6)
. (6)
С учетом (6) формула (4) принимает окончательный вид
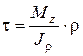 . (7)
. (7)








