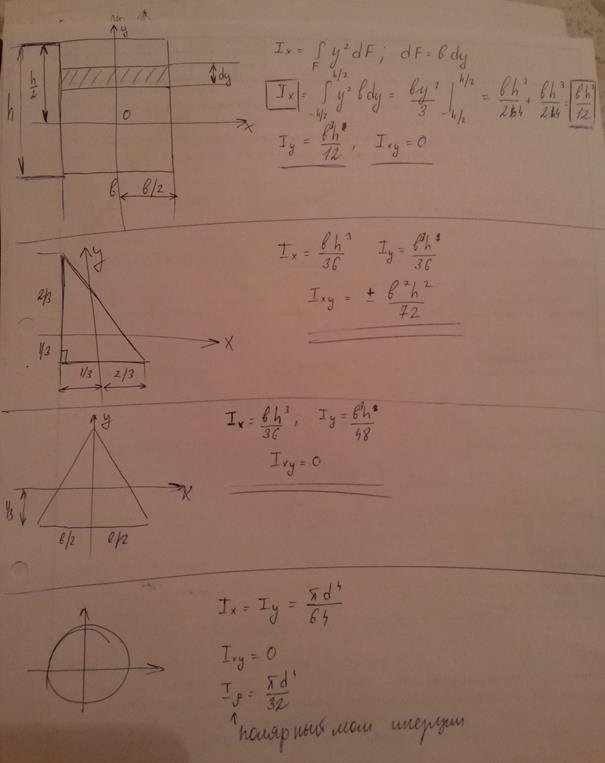
Моменты инерции простых фигур

Дата: 2025-05-25; Просмотры: 5
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

13. Главные оси и главные моменты инерции сечений. Определение положения главных осей и вычисление главных моментов инерции сложных сечений.

Главными осями называются оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции имеют экстремальные значения.

Главные моменты инерции – экстремальные значения моментов инерции. Относительно одной главной оси момент инерции имеет наименьшее значение – Imin, относительно другой – наибольшее Imax.

Будем обозначать главные оси буквами u и v. Докажем приведенное утверждение. Пусть оси x и y – центральные оси несимметричного сечения (рис. 1.1).

Определим положение главных осей путем поворота центральных осей на угол α0, при котором центробежный момент становится равным нулю.

 

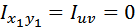
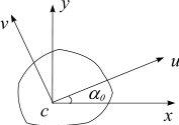
Рисунок 1.1

Тогда

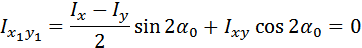
Откуда

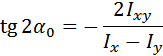
Эта формула определяет положение главных осей, где α0 – угол, на который нужно повернуть центральные оси, чтобы они стали главными. Отрицательные углы α0 откладываются по ходу часовой стрелки от оси x.

Главные центральные моменты инерции определяются по формулам:

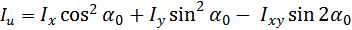
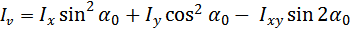
Если сложить почленно эти формулы, очевидно, Iu + Iv = Ix + Iy = const. Если исключить из этих формул угол α0, , то получим более удобную формулу для главных центральных моментов инерции:

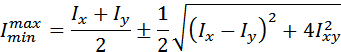
Полезно иметь в виду частные случаи:

1) Если фигура имеет две оси симметрии, то оси являются главными центральными осями.

2) Для правильных фигур – равносторонний треугольник, квадрат, круг и т.п., имеющих более двух осей симметрии, все центральные оси являются главными, а моменты инерции относительно них равны между собой.

 

Общий порядок определения главных центральных моментов инерции

Пусть требуется найти положение главных центральных осей и вычислить относительно них моменты инерции для плоского сечения, состоящего из швеллера и полосы (рис. 1.2):

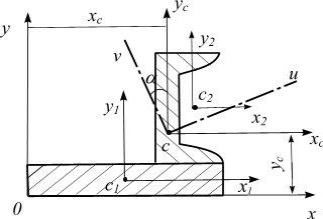
Рисунок 1.2

 

1. Выбирают вспомогательные оси – проводят произвольную систему координат xOy.

2. Разбивают сечение на простые фигуры и по формулам определяют положение центра тяжести С относительно выбранных вспомогательных осей.

3. Через точку С проводят центральные оси x c и yc параллельно осям простых фигур.

4. Определяют осевые центральные моменты инерции простых фигур

Ixc=Ix1+a12F1+ Ix2+ a22F2, где а – расстояние между осями X.

5. Определяют центральные моменты инерции всего сечения как сумму соответствующих моментов простых фигур, найденных в пункте 5.

7. Вычисляют угол α0 по формуле и, поворачивая оси x c и yc на угол α0, изображают главные оси u и v.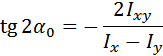

 

8. По формулам вычисляют Imin и Imax.

9. Делают проверку:

а) ;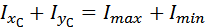

б) ;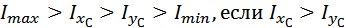

 

14. Кручение круглого вала. Эпюры крутящих моментов, напряжений и углов закручивания по длине вала. Условия прочности и жесткости.