Центр тяжести сечения. Статические моменты сечения
Простейшая геометрическая характеристика – площадь
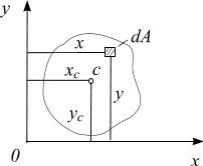
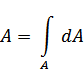
При расчетах на изгиб, кручение, сложное сопротивление, устойчивость используют след геометрические характеристики :
1 Статическим моментом сечения относительно данной оси называется взятая по всей его площади F сумма (интеграл) произведений элементарных площадок d F на их расстояния до этой оси.
Статические моменты площади сечения относительно осей x и y определяются по формулам:
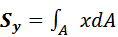
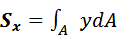
Статические моменты выражаются в см3, м3. В зависимости от знаков координат они могут принимать положительные значения, отрицательные и равные нулю.
Координаты центра тяжести:
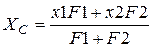
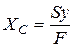
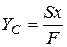
Оси, проходящие через центр тяжести сечения – центральные, статический момент =0.
2 Осевым моментом инерции сечения относительно данной оси называется взятая по всей его площади F сумма произведений элементарных площадок d F на квадраты их расстояний до этой оси. М4
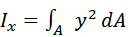
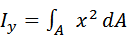
3 Центробежным моментом инерции сечения относительно осей координат x и y называется взятая по всей его площади F сумма произведений элементарных площадок d F на их расстояния до этих осей:
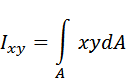
Моменты инерции выражаются в см4, м4.
В зависимости от положения осей центробежный момент инерции может быть положительным, отрицательным или равным нулю.
Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен нулю.
Оси, относительно которых центробежный момент равен нулю, называются главными осями инерции. Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями.
Оси, проходящие через центр тяжести сечения, называется центральными. В этом случае xc =0 и yc =0, тогда Sy = Sx =0. Следовательно, статические моменты относительно центральных осей равны нулю.
4 Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей его площади A сумма произведений элементарных площадок dA на квадраты их расстояний ρ до этой точки. Следовательно:
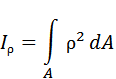
Как видно из рисунка 1.3: ρ2 = x2 + y2, тогда:
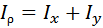
Полярный момент инерции Iρ равен сумме осевых моментов инерции Ix и Iy , взятых относительно любой пары взаимно перпендикулярных осей x и y, проходящих через полюс О.
Отметим, что осевые и полярные моменты инерции всегда положительны.
Для сложных сечений :
1 разбиваем сечение на простые фигуры
2 находим центры тяжести каждой из фигур
3 выбираем вспомогательные оси
4 координаты центров тяжестий С1 и С2 каждой фигуры, относительно вспомогательных осей
5 определяем площади фигур
6 определяем координаты центра тяжести 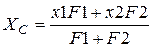
7 находим осевые центральные моменты инерции, относительно х каждой из фигур
8 находим момент инерции составного сечения
Ixcyc=Ix1y1+a1b1F1+Ix2y2+a2b2F2








