Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругом деформировании. При разгрузке она расходуется на восстановление первоначальной формы и размеров тела.
При статическом нагружении работа внешних сил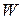 
полностью преобразуется в потенциальную энергию 
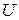, т.е.
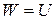. (2.27)
На основании закона Гука график зависимости между растягивающей силой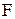 
и удлинением 
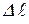в пределах упругих деформаций представляет собой прямую (рис. 2.14).
Определим работу силы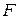 
на перемещении .
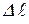Пусть при некотором значении силы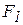 
удлинение бруса равно 
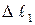. Дадим силе приращение 
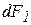, тогда удлинение вырастет на величину 
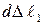. Элементарная работа силы 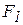на этом перемещении равна
.
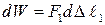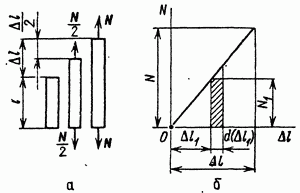
Из рисунка 3.12 видно, что эта величина равна площади узкой заштрихованной полоски графика: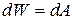 
, поэтому, полная работа
.
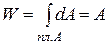Таким образом, работа (а значит, и потенциальная энергия) равна площади заштрихованного треугольника
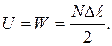(2.28)
Подставляя сюда вместо внешней силы 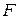равную ей внутреннюю силу 
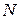и удлинение по формуле (2.24), получим
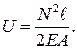(2.29)
E – модуль упругости;
F – площадь поперечного сечения;
L – первоначальная длина стержня
Если поперечное сечение или продольная сила меняются по длине стержня, то потенциальную энергию определяют суммированием по участкам dz :
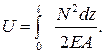(2.30)
Чтобы судить об энергоемкости материала, вводят понятие удельной потенциальной энергии (как потенциальная энергия, приходящаяся на единицу объема бруса):
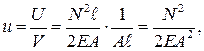
где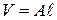 
– объем стержня. С учетом формул (2.5) и (2.3) имеем
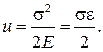(2.31)
В системе СИ за единицу работы и энергии принят джоуль [Дж], тогда удельная энергия деформации выражается в Дж/м3.
Из формулы (2.31) следует, что при одном и том же напряжении запас энергии тем больше, чем меньше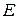 
. Поэтому, например, резина является одним из самых энергоемких материалов, и ее используют в амортизирующих устройствах для смягчения динамических воздействий.
12. Основные геометрические характеристики плоских сечений.
Площадь, статические и осевые, полярный и центробежный моменты инерции; вычисление центра тяжести и моментов инерции составного сечения. Моменты инерции сечений в виде простых фигур: прямоугольника, треугольника, круга и его частей.