Предел временного сопротивления (предела прочности)
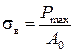. (2.46)
Pmax – максимальная нагрузка, соответствующая условному пределу прочности
A=F – площадь
Временным сопротивлением – максимальное напряжение, которое выдерживает материал без разрушения. Условный – так как делим на начальную площадь.
характеристиками пластичности материала.
1 Относительным остаточным удлинением
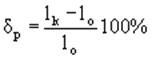
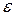(относительная продольная деформация) = … (после испытания)
У пластичных материалов больше 5 процентов.
2 Относительное остаточное сужение образца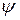 
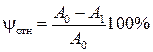, (2.48)
= 
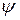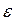(со штрихом – относительная поперечная деформация.)
где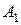 
– площадь поперечного сечения образца в месте разрыва (Площадь шейки после испытаний – из лекции).
Чем больше эти две буквы, тем материал пластичнее.
Пластичность – свойство тел изменять форму и размеры под влиянием внешних нагрузок и сохранять её после снятия нагрузок.
Истинная и условная диаграммы растяжения: Диаграмма растяжения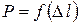 
зависит от размеров образца. Для оценки свойств материала эту диаграмму перестраивают в координатах «напряжение – деформация»; все ординаты делят на первоначальную площадь 
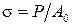, а все абсциссы – на первоначальную рабочую длину 
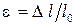. В результате получают диаграмму напряжений 
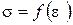(рис. 2.29), которая является условной, т. к. при ее построении не учитывается изменение значений площади сечения 
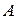в процессе испытания. Поэтому найденные ранее характеристики прочности являются условными.
Рис. 2.29
Диаграмма напряжений, построенная с учетом деления силы на наименьшую площадь – истинных напряжений (на рис. 2.29 она показана пунктиром). Напряжение, соответствующее точке 
, называют истинным сопротивлением разрыву (истинным пределом прочности)
Условный предел текучести:
Если на графике есть DE, то материал точно пластичен.
Для материалов, у которых нет выраженной площадки текучести, но присутствует пластическая деформация, определяют условный предел текучести.
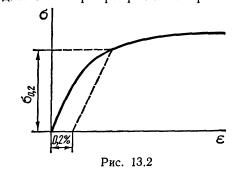
1. Посторим на оси 0.2
2. Проведем касательную к первому участку
3. Прведем линию, паралельную касательной от 0,2 до пересечения с графиком
4. Сносим на оси
Диаграмма сжатия малоуглеродистой стали
ПЛАСТИЧНЫЕ Диаграмма сжатия почти полностью повторяет диаграмму растяжения (рис. 2.32, а).
Пределы пропорциональности, упругости и текучести имеют те же значения, что и при растяжении. Углы наклона прямолинейных участков на обеих диаграммах одинаковы, значит, равны и модули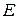 
. Площадка текучести здесь выражена слабо. При дальнейшем нагружении развиваются значительные пластические деформации, образец принимает бочкообразную форму, а затем, не претерпевая разрушения, расплющивается (рис.2.32 в, г). Поэтому получить предел прочности не представляется возможным, и его условно принимают таким же, как при растяжении: 
.
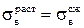Пластичные материалы одинаково сопротивляются растяжению и сжатию.
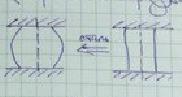
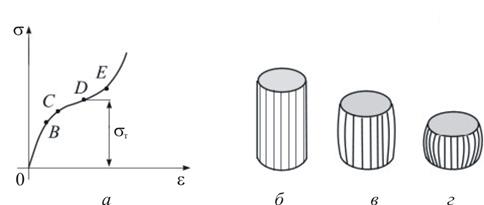
Рис. 2.32
Образцы из других пластичных металлов (медь, алюминий) при сжатии деформируются так же, как стальной, и имеют аналогичную диаграмму.
ХРУПКИЕ. После разрушения трещина под углом 45 градусов. 
Анизотропные материалы: В практике наряду с изотропными материалами, которые являются основным объектом рассмотрения СМ имеют место и анизотропные материалы, т. е. материалы, свойства которых в различных направлениях различны.
Анизотропия может быть начальной (исходной), существующей до процесса нагружения, или вторичной (деформационной), т. е. изменившейся, или заново возникшей в процессе деформации. Можно выделить три типа анизотропии механических свойств: кристаллографическая, технологическая и композиционная.
Пример – дерево, стеклопластик.
Эффект наклепа (Баушингера):
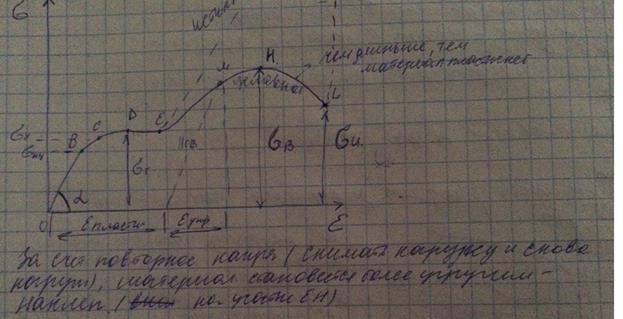
За счет повтороного напряжения( снимать нагрузку и снова нагружать) материал становится более упругим – наклеп(EH)
Если образец нагружен выше предела упругости, то при его разгрузки деформации полностью не исчезают. В этом случае, деформация = упругая+пластическая.При повторном нагружении образца предел пропорциональности повышается до того напряжения до которого образец был ранее нагружен. Это явление называется наклепом.
11. Потенциальная энергия деформации при растяжении-сжатии.
При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U (Работа внешних сил полностью преобразуется в потенциальную).