Перемещения. Эпюра перемещений. Условие жесткости
При растяжении (сжатии) поперечные сечения стержня перемещаются в продольном направлении; перемещения поперечных сечений – это следствие деформации. Перемещение сечения зависит от деформации не всего бруса, а лишь части между сечением и неподвижной заделкой. Например, перемещение сечения равно деформации заштрихованной части стержня: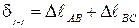 
,
где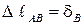 
– деформация участка АВ равная перемещению сечения В;
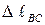– деформация участка ВС определяется по формулам .
можно сформулировать следующие положения:
1. На участке, где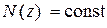 
, перемещение 
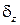– меняется по линейному закону;
2. На участке, где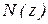 
– линейна, перемещение 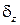– меняется по квадратичной параболе;
3. Если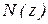 
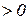, то перемещение 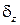возрастает;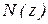 
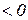, то перемещение 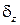убывает;
4. В сечении, где =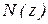 
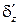=0, перемещение 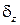имеет экстремальное значение: 
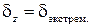(максимум или минимум).
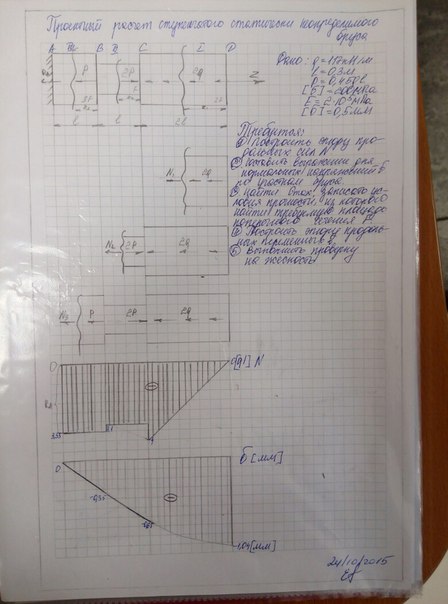
9. Статически неопределимые задачи при растяжении-сжатии, методы их решений.
В практике статически неопределимые задачи находят широкое применение.
Система, в которой для определения внутренних усилий недостаточно уравнений равновесия называется статические неопределимой.
Для решения данной задачи необходимо применение дополнительных уравнений, которые можно записать, рассмотрев деформированное состояние системы. Дополнительные уравнения представляют собой уравнения совместности деформаций (или кратко называются деформационными).
Расчет статически неопределимой системы рассмотрим на примере статически неопределимого ступенчатого бруса.
Степень статической неопределимости :
S=R-n
R – количество связей
n – количество возможных уравнений
1. Сумма Ркz=0
2. ∆l1+∆ l2+∆ l3=0 – дополнительное уравнение неразрывности деформации
10. Опытное изучение свойств материалов при растяжении и сжатии. Диаграммы растяжения и сжатия малоуглеродистой стали. Основные механические характеристики и характеристики пластичности материалов: предел пропорциональности, упругости, текучести, временное сопротивление (предел прочности), относительное удлинение и сужение площади поперечного сечения. Истинная и условная диаграммы растяжения. Условный предел текучести. Диаграммы сжатия хрупких и пластичных материалов. Анизотропные материалы. Эффект наклепа (Баушингера).
При проектировании и расчетах на прочность и жесткость необходимо знать свойства материалов, сведения о которых можно получить путем механических испытаний на растяжение, сжатие, сдвиг, кручение и изгиб.
Испытание на растяжение проводят на специальных разрывных или универсальных машинах, создающих постепенно возрастающую нагрузку на образец. Машины снабжены устройством для автоматической записи диаграммы растяжений, т. е. графика зависимости между растягивающей силой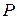 
и удлинением образца 
.
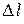Рассмотрим характерные участки и точки этой диаграммы, а также соответствующие им стадии деформирования образца.
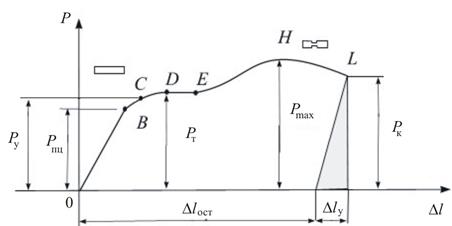
Рис. 2.27
OB – выполняется прямая пропорциональная зависимость между нагрузкой и абсолютной деформацией (только упругой)
Выполняется закон Гука.
,
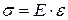где E (МПа) – физическая константа материала, называемая модулем продольной упругости или модулем упругости первого рода, характеризующая жесткость материала. Значения модуля упругости зависят от типа кристаллической решетки и межатомного взаимодействия и определяются экспериментально.
Pпц – нагрузка, соответствующая пределу пропорциональности.
ВС – нарушение пропорциональной зависимости (деформации еще упругие)
CD – появление пластической деформации.
DE – площадка текучести(рост деформации без увеличения нагрузки, параллельно оси). Наличие площадки текучести связано с развитием сдвигов в кристаллической решетке.
EH – зона упрочнения (явление наклепа)
HL – зона образования шейки
Py – нагрузка, соответствующая пределу упругости
PT – предел текучести
Pmax – максимальная нагрузка, соответствующая условному пределу прочности
Pu – нагрузка, соответствующая истинному напряжению в точки разрыва.
Прямая пропорциональная зависимость между напряжением и деформацией сохраняется до напряжений, соответствующих пределу пропорциональности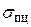 
, который определяется делением соответствующей нагрузки на начальную площадь образца 
:
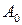Pпц – нагрузка, соответствующая пределу пропорциональности.
A=F – площадь
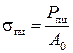
Предел пропорциональности – максимальное напряжение, выше которого нарушается прямая пропорциональная зависимость между напряжением и деформацией.
Упругие свойства материала сохраняются до напряжения, называемого пределом упругости. Под пределом упругости понимается такое наибольшее напряжение, до которого в образце еще отсутствуют пластические деформации.
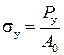. (2.44)
Py – нагрузка, соответствующая пределу упругости
A=F – площадь
Пределом упругости – максимальное напряжение, до которого нет пластической деформации.
Пределом текучести.
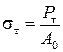. (2.45)
PT – предел текучести
A=F – площадь
Предел текучести – после достижения предела текучести появляется интенсивная пластическая деформация.