Расчет по допускаемым напряжениям ведется в пределах упругих деформаций. Применяется при проектировании деталей машин и механизмов.
Закон Гука. Модуль упругости: Английский ученый Роберт Гук в 1678 г. на основе экспериментов с проволокой и пружинами сформулировал закон “Ut tensio, sic vis”, т.е. “Каково удлинение, такова и сила”.
В 1822 г. французский математик Луи Коши ввел понятия напряжение и деформация. В современном виде закон Гука формулируется так:
Относительная продольная деформация прямо пропорциональна соответствующему нормальному напряжению
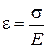, (2.19)
где E – модуль продольной упругости (модуль Юнга), упругая постоянная материала, характеризующая жесткость материала при растяжении (сжатии); определяется экспериментально, имеет размерность напряжения, например:
для стали Е = 2´105 МПа, алюминиевых сплавов Е = 0,65´105 МПа, для резины E = 7,0 МПа, для дерева Е = 104 МПа, для бетона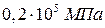 
.
Идею о модуле упругости впервые высказал в 1800 г. английский ученый Томас Юнг. Он же первый указал, что закон Гука справедлив только в пределах упругих деформаций материала.
На рисунке 2.8, а дано графическое представление закона Гука. Установим геометрический смысл модуля упругости Е. Выберем точку В прямолинейного участка ОВ (рис. 2.10,а), координаты этой точки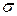 
и 
.
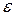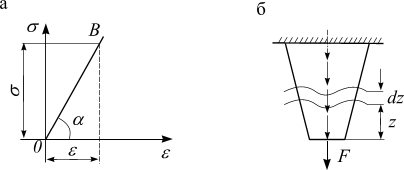
Рис. 2.8
Очевидно, их отношение (тангенс угла наклона линии ОВ к оси абсцисс) равно модулю продольной упругости :
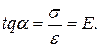
Перейдем к определению деформаций стержня. Из формул (2.4) и (2.6) имеем:
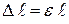и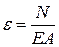 
.
Тогда абсолютное удлинение участка стержня длиной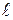 
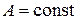при 
и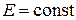 
будет равно
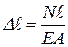, (2.20)
где EA - жесткость поперечного сечения при растяжении (сжатии). Формула (2.20) выражает закон Гука для абсолютной продольной деформации, ее называют формулой жесткости при растяжении и сжатии.
8. Продольные и поперечные деформации бруса при растяжении (сжатии). Коэффициент Пуассона. Перемещения и их эпюры.
Если на участке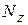 
и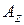 
переменны (рис. 2.8 б), то полное удлинение участка 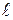получим, суммируя удлинения бесконечно малых участков dz:
.
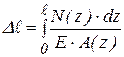Растяжение (сжатие) сопровождается изменением поперечных размеров (рис. 2.9).
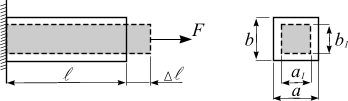
Рис. 2.9
Абсолютная поперечная деформация определяется как разность размеров после деформации и до нее:
; 
.
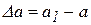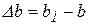Относительная поперечная деформация для изотропных материалов по всем направлениям одинакова:
.
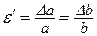Между поперечной и продольной относительными деформациями, которые всегда противоположны по знаку, в пределах закона Гука существует постоянное отношение:
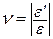или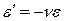 
, (2.23)
где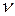 
– коэффициент поперечной деформации (коэффициент Пуассона) – безразмерная величина, упругая постоянная материала, определяемая экспериментально. Для всех изотропных материалов 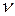= 0 ¸ 0,5. Для пробки 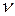»0; для каучука 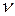» 0,5; для стали 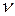» 0,3.