Напряжения в наклонных сечениях
Рассечем растянутый стержень плоскостью, наклоненной к поперечному сечению под углом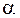 
(рис. 2.6, а), и рассмотрим нижнюю часть стержня (рис. 2.6, б). Из условий ее равновесия следует, что напряжения 
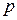параллельны оси бруса, а внутренняя сила 
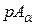, возникающая в сечении, равна F. Здесь 
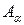- площадь наклонного сечения равная 
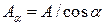. Следовательно, 
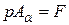, откуда
,
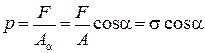где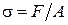 
– нормальное напряжение в поперечном сечении.
Выделим малый элемент в наклонном сечении (рис. 2.6, а,б) и раскладывая р по нормали и касательной к сечению (рис. 2.6, в), находим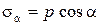 
и 
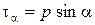. С учетом выражения для р получаем
= 
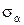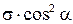, (2.9)
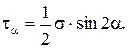(2.10)
Следовательно, при растяжении (сжатии) в наклонных сечениях возникают нормальные и касательные напряжения.
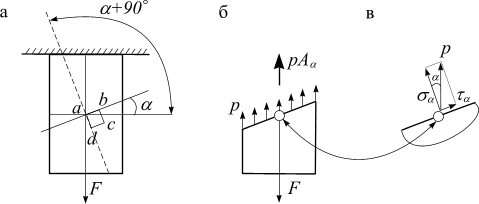
Рис. 2.6
Из формул (2.9) и (2.10) следует:
1. В поперечных сечениях, т.е. когда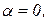 
имеем
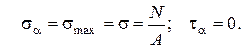
Нормальные напряжения в поперечных сечениях будут наибольшими, а касательные напряжения равны нулю.
2. В продольных сечениях, т.е. при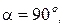 
нормальные и касательные напряжения равны нулю:
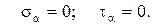
Отсюда следует, что продольные слои не испытывают взаимного давления и взаимного сдвига при растяжении и сжатии.
3. На площадках, наклоненных под углом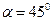 
, имеем
,
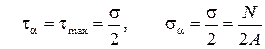т.е. касательные напряжения будут максимальными, а нормальные напряжения будут им равными.
Следует отметить, что на двух взаимно перпендикулярных площадках касательные напряжения равны по абсолютной величине. Действительно, по формуле (2.10) получаем:
,
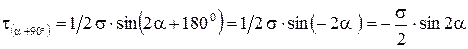т.е.
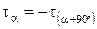. (2.11)
Формула (2.11) выражает закон парности касательных напряжений: на двух взаимно перпендикулярных площадках, составляющие касательных напряжений, перпендикулярные к общему ребру, равны и направлены обе либо к ребру, либо от ребра.
Этому можно дать наглядное толкование, если из растянутого стержня в окрестности некоторой точки выделить бесконечно малый прямоугольный элемент abcd (рис. 2.6, а), к граням которого приложены напряжения, заменяющие действия отброшенных частей тела (рис. 2.7). Касательные напряжения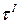 
и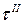 
должны быть такой величины и иметь такое направление, чтобы моменты их пар взаимно уравновешивались.
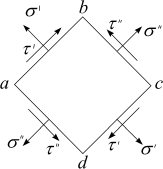
Рис. 2.7
Причем для одной и той же точки напряжения различны в зависимости от ориентации секущей площадки.
Построение эпюр нормальных напряжений:
Условие прочности: Основные задачи расчетов на прочность:
- определение оптимальных геометрических размеров элементов конструкций, обеспечивающих их прочность;
- определение несущей способности, т. е. установление допускаемых или предельных нагрузок, которые может выдержать конструкция, не разрушаясь;
- обеспечение способности конструкции удовлетворять заданным эксплуатационным требованиям.
Для решения этих задач разработано три метода расчетов:
1. Расчет по допускаемым напряжениям;
2. Расчет по разрушающим (предельным) нагрузкам;
3. Расчет по предельным состояниям.