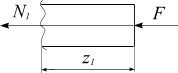
Расчетное напряжение - наибольшее по абсолютной величине сжимающее или стягивающее напряжение, возникающее в опасном сечении конструкции.

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Качество конструкции сейчас оценивают запасом прочности, под которым понимается

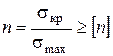, (1.7)

здесь 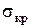– критическое значение параметра, нарушающее работоспособность (например, параметры коррозии, старения и др.),

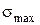– наибольшее значение этого параметра при работе конструкции,

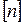– допустимое значение запаса, которое назначается, исходя из опыта эксплуатации, например, при случайных нагрузках .

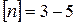Необходимо, чтобы наибольшее напряжение, полученное в результате расчета конструкции (расчетные напряжения), не превышали некоторой величины, меньше предела прочности, называемой допускаемым напряжением.

5. Понятие о деформациях (линейных и угловых, абсолютных и относительных) и перемещениях. Общий вид условия жесткости.

Коэффициент Пуассона — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент полностью характеризуют упругие свойства изотропного материала

Перемещение — изменение положения точки тела в пространстве вследствие изменения его формы и размеров под действием нагрузки.

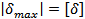- условие жесткости

6. Осевое растяжение и сжатие прямого стержня. Определение. Продольные силы. Построение эпюр продольных сил.

Осевым (центральным) растяжением или сжатием называют такой вид деформации, при котором в поперечном сечении бруса возникают только продольная сила N(растягивающая или сжимающая), а все остальные внутренние усилия равны 0.

Построение эпюры продольных сил

Продольная сила N в сечении численно равна алгебраической сумме проекций на ось Z всех внешних сил, включая и опорные реакции, действующие на отсеченную часть бруса, взятых со знаком плюс, если они направлены от сечения (растяжение), и минус – если к сечению (сжатие):

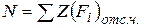(2.2)

Знак продольной силы 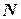определяется по схеме: растяжение – со знаком «+»,сжатие – со знаком «–» .

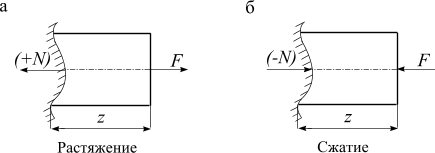
Рис. 2.2

Пример 2.1. Для бруса (рис. 2.3, а) построить эпюру продольных сил N.

1. Определим реакцию заделки.

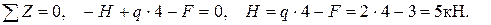
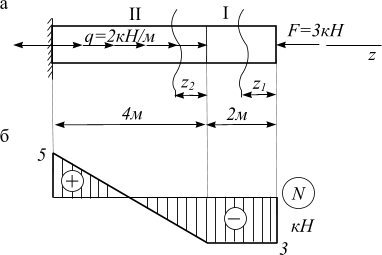
Рис. 2.3

2. Разобьем брус на два участка, и, применив метод сечений, найдем продольные силы на каждом из них, рассматривая равновесие отсеченной части. Во избежание ошибки следует внутреннее усилие принимать всегда положительным (направлять от сечения).

Участок I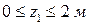

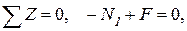
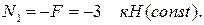
На первом участке продольная сила постоянна и отрицательна.

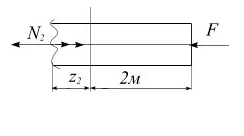Участок II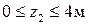

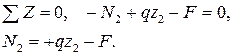
На этом участке продольная сила изменяется по линейному закону.

при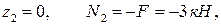

при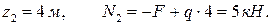

По найденным значениям продольных сил на отдельных участках строим эпюру N (рис. 2.3, б).

Примечание

1. Для бруса, закрепленного с помощью заделки, для построения эпюры, не обязательно определение опорных реакций, если оставлять часть бруса, которая не закреплена.

2. Знак усилия 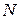, получаемый из решения, позволяет установить вид деформации – растяжение или сжатие.

3. На участке I, где 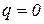, эпюра N – прямая, параллельная оси ).

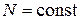4. На участке II, где 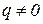, эпюра N – наклонная прямая (N изменяется по линейному закону).

5. В сечениях, где приложены внешние силы, внутренняя сила меняется скачкообразно, причем размер скачка равен соответствующей внешней силе. Так, скачок на уровне заделки характеризует значение реакции (Н=5 кН), скачок на свободном конце – значение внешней силы ( F =3 кН).

7. Напряжение в поперечных и наклонных сечениях прямого стержня при растяжении (сжатии). Построение эпюр нормальных напряжений. Условие прочности. Закон Гука. Модуль упругости.

Продольная сила N, возникающая в поперечном сечении бруса, представляет собой равнодействующую внутренних нормальных сил, распределенных по площади поперечного сечения, и связана с возникающим в этом сечении нормальными напряжениями зависимостью :

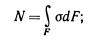
Вывод формул для напряжений в стержнях будем всегда проводить по приведенной ниже схеме:

1.

Статическая сторона задачи – запись интегральных уравнений равновесия;

2.

Геометрическая сторона задачи – изучение деформаций на основе опыта и гипотез;

3. Физическая сторона задачи определяется законом Гука;

4. Синтез – совместное решение полученных уравнений.