Каждому из внутренних усилий соответствует простой вид сопротивления (нагружения) бруса.
Продольной силе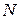 
– растяжение или сжатие, поперечной силе 
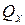или 
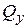– сдвиг, крутящему моменту 
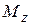– кручение, а изгибающим моментам 
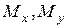– изгиб.
Если в поперечном сечении возникает только один внутренний силовой фактор сопротивление называется простым (растяжение, сжатие, кручение, прямой изгиб).
Прямой изгиб – исключение, т.к при этом виде сопротивления возникает два силовых фактора ( поперечная сила, изгибающий момент).
Прямой изгиб относится к простым, т.к расчеты на прочность только по изгибающему моменту.
Сложное сопротивление – в поперечном сечении возникает более одного силового фактора ( косой изгиб, изгиб с кручением)
4. Понятия о напряжениях (нормальных, касательных, полных) и их связь с внутренними усилиями. Общий вид условия прочности. Понятие о допускаемом напряжении. Коэффициенты запаса.
Понятия о напряжениях (нормальных, касательных, полных) и их связь с внутренними усилиями:
Мерой распределения внутренних сил по сечению элемента конструкции является напряжение.
Внутренняя сила, приходящаяся на единицу площади в данной точке, называется напряжением.
Рассмотрим отсеченную часть бруса. В окрестности точки К выделим элементарную площадку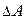 
, в пределах которой равнодействующая внутренних сил равна 
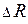(некоторая часть главного вектора 
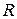) (рис.1.6).
Отношение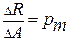 
представляет собой среднее напряжение на площадке 
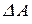. В пределе получаем
,
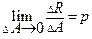
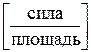где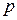 
–полное напряжение в точке K площади ΔА.
В системе СИ напряжение выражается в паскалях Па=Н/м2 или мегапаскалях МПа=106 Па.
, 
, 
,
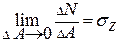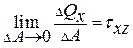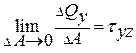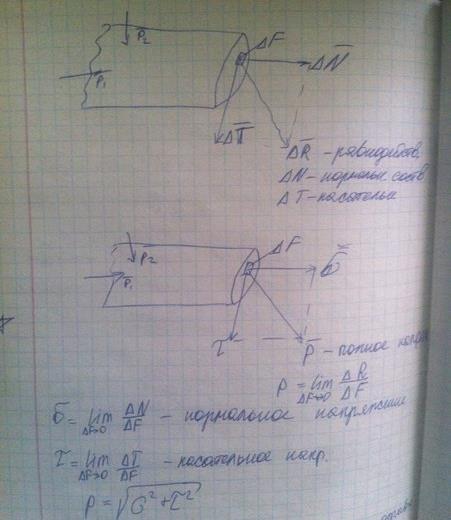
где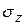 
– нормальное напряжение; характеризует интенсивность сил отрыва либо сжатия
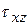и 
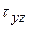– касательные напряжения; характеризует интенсивность сдвиговх сил.
Тогда напряжение 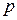можно рассматривать как полное напряжение в точке на данной площадке:
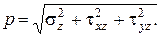(1.3)
Сигма – характеризуют интенсивность сил отрыва либо сжатия.
Тау – характеризуют интенсивность сдвиговых сил
Совокупность норм и касат. напряжений, действующих по различным площадкам, проходящим через данную точку, называется напряженным состоянием в этой точке. Вычисление напряжений является основой расчетов на прочность.
Нормальные и касательные напряжения в каждом поперечном сечении тела связанны с определенными зависимостями :
Интегральные зависимости между внутренними
силовыми факторами и напряжениями
Пусть в некоторой точке бесконечно малой площадки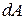 
выявлены напряжения 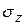, , 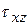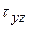(рис. 1.7).
Просуммировав напряжения по площадке 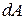, получим элементарные внутренние усилия:
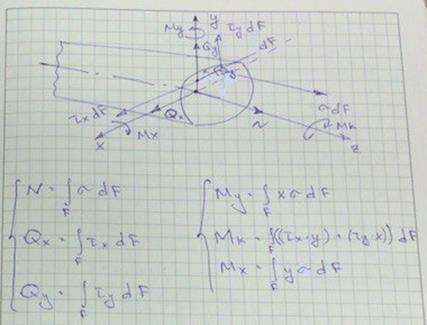Выражения называются интегральными уравнениями равновесия или статическими уравнениями.
Записанные статические уравнения не позволяют определить напряжения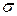 
и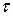 
, пока не установлен закон их распределения по сечению.
Общий вид условия прочности: Нахождение вероятности разрушения на стадии проектирования в настоящее время еще сложная задача.
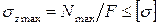
Сравнению расчетных напряжений с допускаемыми: 
- основные условия прочности.