По способу приложения нагрузки сводят к распределенным и сосредоченным силовым воздействием.
Сосредоточенные нагрузки F, M – силы и моменты, площадь действия которых мала по сравнению с размерами объекта (приложены в точке).
Распределенная нагрузка q – сила, действующая на некоторой длине стержня.
В тех случаях, когда площадка контакта реальных тел пренебрежимо мала по сравнению с размерами нагружаемого элемента, вводят понятие сосредоточенной силы F [H] как равнодействующей давления по указанной площадке.
По длительности действия внешние нагрузки делятся на :
-постоянные;
-временные.
К постоянным относятся нагрузки, действующие в течение всего времени существования конструкции или сооружения (вес несущих и ограждающих конструкций, вес и давление грунта).
Временные нагрузки действуют на протяжении отдельных периодов эксплуатации или возведения объекта
По характеру действия делятся на :
-статические;
-динамические.
К статическим (медленно возрастающая от 0 до некоторого значения) относятся нагрузки не изменяющиеся со временем или меняющиеся настолько медленно, что вызываемые ими ускорения и силы инерции элементов пренебрежимо малы.
Динамические нагрузки меняют свое значение, положение или направление в короткие промежутки времени (движущиеся нагрузки, ударные, сейсмические и др.), вызывая большие ускорения и силы инерции, что приводит к колебаниям конструкций и сооружений (удар, вращение).
Повторно-переменные нагрузки многократно (до нескольких миллионов раз) изменяют со временем значение или значение и знак. Разрушение материала под действием таких нагрузок называется усталостным (например, разрушение куска проволоки от многократного перегибания)
Расчетная схема - это упрощенная, идеализированная схема, которая отражает наиболее существенные особенности объекта, определяющие его поведение под нагрузкой.
Формы элементов конструкций, используемых в расчетных схемах, можно свести к четырем категориям: стержню(брус), оболочке, пластине и массивному телу.
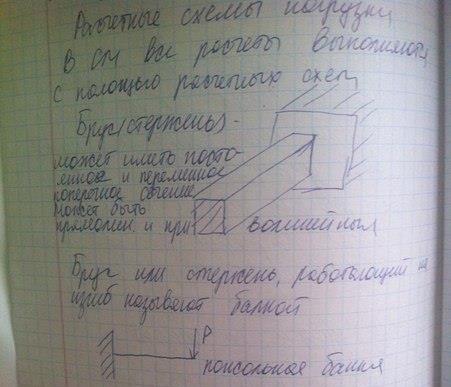
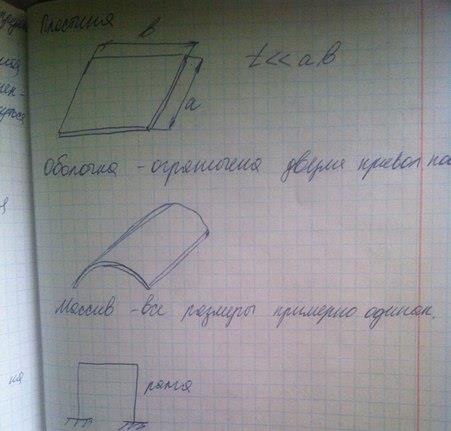
Брус – тело, у которого один размер (длина) значительно превышает два других размера.
Может иметь постоянное и переменное поперечное сечение. Может быть прямолинейным, а может криволинейным.
Оболочка – ограниченна двумя криволинейными поверхностями.
Массив – тело, все размеры которого примерно одинаковы.
Основные типы связей
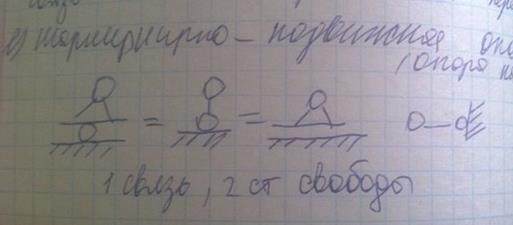
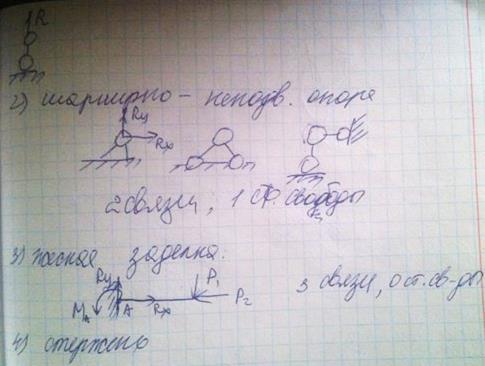
Внутренние усилия. Метод сечений:. Под действием внешних сил тело деформируется. При этом возникают дополнительные внутренние силы, которые отражают сопротивление материала деформированию и разрушению. В курсе СМ принимают во внимание и определяют внутренние силы, которые возникают при нагружении тела внешними силами. Для определения внутренних сил применяется метод сечений.
Пусть на брус действует система взаимно уравновешенных внешних сил F1, F2… Fn (1.5, а). Для определения внутренних сил производят последовательно четыре операции:
1. Рассекают брус в интересующем месте воображаемой плоскостью на две части
2. Отбрасывают мысленно одну из образовавшихся частей
3. Заменяют действие отброшенной части I на оставшуюся II внутренними силами. При этом имеют в виду, что внутренние силы согласно правилам теоретической механики могут быть приведены к центру тяжести и, таким образом заменены главным вектором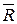 
и главным моментом 
.
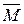Каждый из этих двух статических эквивалентов внутренних сил можно представить в виде трех составляющих по осям выбранных координат x, y, z.
N – продольная (нормальная) сила;
, 
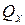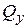– поперечные силы вдоль осей х и у;
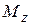– крутящий момент;
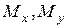– изгибающие моменты относительно осей х и у.
Эти компоненты главного вектора и главного момента называются внутренними силовыми факторами или усилиями (ВУ).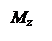 
4 Для определения внутренних усилий составляют уравнения равновесия всех сил, приложенных к оставшейся части II :
, 
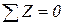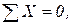
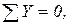
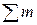
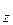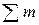
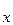=0, 
=0,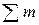 
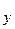=0. (1.1)
Вычисляя внутренние усилия и моменты в сечении по формулам (1.2), следует иметь в виду:
– что продольная сила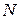 
численно равна алгебраической сумме проекций всех внешних сил, действующих на одну из частей (I или II) рассеченного бруса, на продольную ось z ; 
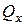– то же на ось x; 
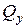– то же на ось y;
– крутящий момент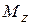 
численно равен алгебраической сумме моментов всех внешних сил, действующих на одну из частей (I или II) относительно оси бруса z; 
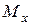– то же относительно оси x; 
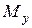– то же относительно оси y.
Таким образом, метод сечений позволяет найти все внутренние усилия и моменты в любом сечении бруса при действии любой нагрузки.