Постулаты булевой алгебры
Вначале приведем формальный список постулатов булевой алгебры, а потом – некоторые комментарии.
| Операции с константами: | |
| x+0=x | x·1=x |
| x+1=1 | x·0=0 |
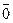 =1 =1
| 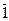 =0 =0
|
| Закон исключенного третьего: | Закон противоречия: |
x+ 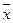 =1 =1
| x· 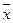 =0 =0
|
| Закон двойного отрицания: | |
|
| |
| Закон идемпотентности (повторения): | |
| x+x=x | x·x=x |
| Коммутативный закон: | |
| x1+x0=x0+x1 | x1·x0=x0·x1 |
| Ассоциативный закон: | |
| x2+(x1+x0)=(x2+x1)+x0 | x2 (x1·x0)= (x2 x1)·x0 |
| Дистрибутивный закон: | |
| x2+x1·x0=(x2+x1)·(x2+x0) | x2 (x1+x0)=x2 x1+x2 x0 |
| Теорема де Моргана: | |
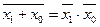
| 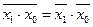
|
| Закон поглощения: | |
| x1+x1·x0= x1 | x1 (x1+x0)= x1 |
| Закон склеивания: | |
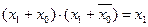
| 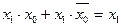
|
Ну, а теперь некоторые комментарии.
Видно, что за исключением одного постулата, остальные расположены в две колонки, причем так делается во всех изданиях. Этим подчеркивают дуализм булевой алгебры. Кто не знаком со словом дуализм, можно напомнить, что в курсе общей физике они наверняка должны были сталкиваться с корпускулярной и волновой теориями света – то есть с дуализмом фотонов. В булевой алгебре в качестве альтернативы выступают дизъюнкция и конъюнкция.
Секция «Операции с константами» представляет собой просто другую формулировку операций конъюнкции и дизъюнкции (проведите сравнительный анализ этой секции с соответствующими таблицами истинности).
В принципе, этой секции достаточно, чтобы обосновать все остальные соотношения. В булевой алгебре для этого используется метод совершенной индукции (у тех, кто интересовался математикой, в памяти должны всплыть счастливые школьные годы и слова «метод математической индукции»). Метод совершенной индукции заключается в том, что какие-либо соотношения проверяются (доказываются) подстановкой всех возможных значений переменных (благо в булевой алгебре их всего два). Попробуем, например, доказать закон двойного отрицания.
Пусть x=0, тогда в соответствии с постулатами, касающимися констант (или, если угодно по определению операции отрицания) 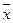 =1. Если еще раз применить операцию НЕТ, получим
=1. Если еще раз применить операцию НЕТ, получим 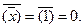 Таким образом, для x=0
Таким образом, для x=0 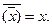
Пусть x=1. Тогда по аналогии с вышеприведенными рассуждениями имеем 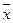 =0,
=0, 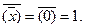 Таким образом, этот постулат верен и для x=0 и для x=1, то есть он верен всегда (в рамках булевой алгебры!). Как догадались наиболее проницательные читатели, теперь следует с помощью метода совершенной индукции доказать (подтвердить) все приведенные постулаты. По секрету могу сказать, что это вполне может пригодиться на экзамене.
Таким образом, этот постулат верен и для x=0 и для x=1, то есть он верен всегда (в рамках булевой алгебры!). Как догадались наиболее проницательные читатели, теперь следует с помощью метода совершенной индукции доказать (подтвердить) все приведенные постулаты. По секрету могу сказать, что это вполне может пригодиться на экзамене.
Для законов коммутативности, ассоциативности и дистрибутивности все выглядит очень привычно, за исключением закона дистрибутивности для дизъюнкции. Хотя он и выглядит весьма непривычно для человека, воспитанного на классической алгебре, ему следует отдать должное внимание. Попробуем доказать дистрибутивный закон для дизъюнкции аналитически с помощью ранее описанных постулатов (с помощью метода совершенной индукции, я уверен, Вы уже его доказали!!!).
Будем доказывать, что правая часть действительно равна левой части. Сначала к правой части два раза последовательно применим дистрибутивный закон для конъюнкции
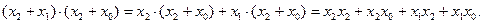
| (23) |
Далее воспользуемся такими соотношениями: x2x2=x2=1×x2 (обязательно найдите в списке постулатов соответствующие строчки!). Тогда из (23) имеем:
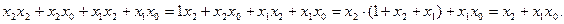
| (24) |
Здесь также использованы постулаты 1+x=1 и еще раз x·1=x.
Аналогично следует доказать законы поглощения и повторения.
Особое место в списке постулатов занимает теорема де Моргана. Она не имеет аналогов в обычной алгебре. Важность теоремы де Моргана обусловлена тем, что с её помощью можно осуществлять переход от дизъюнкции к конъюнкции и наоборот. Попробуйте прочитать эту теорему вслух, и Вы увидите, что в ней есть что-то очаровывающее. На самом деле, попробуйте в кругу знакомых задумчиво произнести: «Инверсия дизъюнкции есть конъюнкция инверсий» или «Инверсия конъюнкции есть дизъюнкция инверсий» и отследите реакцию окружающих….
А теперь сравните, сколько страниц мы потратили на знакомство с основами булевой алгебры, и сколько строчек на это тратится в японских учебниках. Теперь Вы поняли, почему в Японии делают такие маленькие сотовые телефоны?
Поскольку логические переменные принимают только 2 значения, то это позволяет удобно связать логические высказывания с двоичными цифрами в двоичной системе счисления, что и дает возможность описывать поведение цифровых схем с помощью булевой алгебры (алгебры логики). Любое цифровое устройство можно рассматривать как функциональный преобразователь, входными данными для которого служат логические переменные, а выходная функция тоже принимает 2 значения: 0 и 1.
Функция F(Xn-1 Xn-2 … X0), определяемая на наборах входных двоичных переменных Хn-1, Хn-2 Х0 и принимающая в качестве возможных значений 0 или 1 называется логической функцией или функцией алгебры логики. Но подробнее об этом мы будем говорить на живых лекциях.
Список использованных источников
1. Фрэнк Т.С. PDP-11: Архитектура и программирование: Пер. с англ. – М.: Радио и связь, 1986. – 376 с.: ил.
2. Математика: Учебник для 5 кл. общеобразовательных учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 5-е изд., испр. и доп. – М.: Издательство «Русское слово», 1997 – 358 с. ил.
3. Хоровиц П., Хилл У. Искусство схемотехники: В 3-х томах: Т. 2. Пер. с англ. – 4-е изд., перераб. и доп. – М.: Мир, 1993. – 371 с., ил.
4. Киносита К., Асада К., Карацу О. Логическое проектирование СБИС: Пер. с япон. – М.: Мир, 1988 – 309 с.