4.10. Расчет изгибаемых элементов на прочность по скалыванию следует выполнять по формуле

Дата: 2025-05-25; Просмотры: 5

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

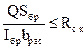, (18)

где Q – расчетная поперечная сила;

S_бр – статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;

I_бр – момент инерции брутто поперечного сечения элемента относительно нейтральной оси;

b_рас – расчетная ширина сечения элемента;

R_ск – расчетное сопротивление скалыванию при изгибе.

4.11. Количество срезов связей n_с, равномерно расставленных в каждом шве составного элемента на участке с однозначной эпюрой поперечных сил, должно удовлетворять условию

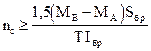, (19)

где Т – расчетная несущая способность связи в данном шве;

М_А, М_В – изгибающие моменты в начальном А и конечном В сечениях рассматриваемого участка.

Примечание. При наличии в шве связей разной несущей способности, но одинаковых по характеру работы (например, нагелей и гвоздей), несущие способности их следует суммировать.

4.12. Расчет элементов цельного сечения на прочность при косом изгибе следует производить по формуле

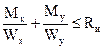, (20)

где М_х и М_у – составляющие расчетного изгибающего момента для главных осей сечения Х и У;

W_x и W_у – моменты сопротивлений поперечного сечения нетто относительно главных осей сечения Х и У.

4.13. Клееные криволинейные элементы, изгибаемые моментом М, уменьшающим их кривизну, следует проверять на радиальные растягивающие напряжения по формуле

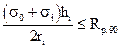, (21)

где s₀ – нормальное напряжение в крайнем волокне растянутой зоны;

s_i – нормальное напряжение в промежуточном волокне сечения, для которого определяются радиальные растягивающие напряжения;

h_i – расстояние между крайним и рассматриваемым волокнами;

r_i – радиус кривизны линии, проходящей через центр тяжести части эпюры нормальных растягивающих напряжений, заключенной между крайним и рассматриваемым волокнами;

R_р.90 – расчетное сопротивление древесины растяжению поперек волокон, принимаемое по п. 7 табл. 3.

4.14. Расчет на устойчивость плоской формы деформирования изгибаемых элементов прямоугольного постоянного сечения следует производить по формуле

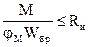, (22)

где М – максимальный изгибающий момент на рассматриваемом участке l_р;

W_бр – максимальный момент сопротивления брутто на рассматриваемом участке l_p.

Коэффициент j_М для изгибаемых элементов прямоугольного постоянного поперечного сечения, шарнирно-закрепленных от смещения из плоскости изгиба и закрепленных от поворота вокруг продольной оси в опорных сечениях, следует определять по формуле

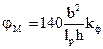, (23)

где l_p – расстояние между опорными сечениями элемента, а при закреплении сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба – расстояние между этими точками;

b – ширина поперечного сечения;

h – максимальная высота поперечного сечения на участке l_p;

k_ф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке l_p, определяемый по табл. 2 прил. 4 настоящих норм.

При расчете изгибаемых элементов с линейно меняющейся по длине высотой и постоянной шириной поперечного сечения, не имеющих закреплений из плоскости по растянутой от момента М кромке, или при m < 4 коэффициент j_М по формуле (23) следует умножать на дополнительный коэффициент k_жМ. Значения k_жМ приведены в табл. 2 прил. 4. При m ³ 4 k_жМ = 1.

При подкреплении из плоскости изгиба в промежуточных точках растянутой кромки элемента на участке l_p коэффициент j_М определенный по формуле (23), следует умножать на коэффициент k_пМ:

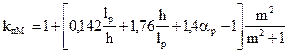, (24)

где a_p – центральный угол в радианах, определяющий участок l_p элемента кругового очертания (для прямолинейных элементов a_p = 0);

m – число подкрепленных (с одинаковым шагом) точек растянутой кромки на участке l_p (при m ³ 4 величину 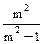следует принимать равной 1).

4.15. Проверку устойчивости плоской формы деформирования изгибаемых элементов постоянного двутаврового или коробчатого поперечного сечений следует производить в тех случаях, когда

l_p ³ 7b, (25)

где b – ширина сжатого пояса поперечного сечения.

Расчет следует производить по формуле

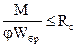, (26)

где j – коэффициент продольного изгиба из плоскости изгиба сжатого пояса элемента, определяемый по п. 4.3;

R_с – расчетное сопротивление сжатию;

W_бр – момент сопротивления брутто поперечного сечения; в случае фанерных стенок – приведенный момент сопротивления в плоскости изгиба элемента.

Элементы, подверженные действию осевой силы с изгибом

4.16. Расчет внецентренно-растянутых и растянуто-изгибаемых элементов следует производить по формуле

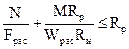, (27)

где W_рас – расчетный момент сопротивления поперечного сечения (см. п. 4.9);

F_рас – площадь расчетного сечения нетто.

4.17. Расчет на прочность внецентренно-сжатых и сжато-изгибаемых элементов следует производить по формуле

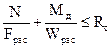, (28)

где М_д – изгибающий момент от действия поперечных и продольных нагрузок, определяемый из расчета по деформированной схеме.

Примечания: 1. Для шарнирно-опертых элементов при симметричных эпюрах изгибающих моментов синусоидального, параболического, полигонального и близких к ним очертаний, а также для консольных элементов М_д следует определять по формуле

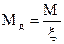, (29)

где x – коэффициент, изменяющийся от 1 до 0, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, определяемый по формуле

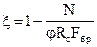, (30)

М – изгибающий момент в расчетном сечении без учета дополнительного момента от продольной силы;

j – коэффициент, определяемый по формуле (8) п. 4.3.

2. В случаях когда в шарнирно-опертых элементах эпюры изгибающих моментов имеют треугольное или прямоугольное очертание, коэффициент – по формуле (30) следует умножать на поправочный коэффициент k_н:

k_н = a_н + x(1 – a_н), (31)

где a_н – коэффициент, который следует принимать равным 1,22 при эпюрах изгибающих моментов треугольного очертания (от сосредоточенной силы) и 0,81 при эпюрах прямоугольного очертания (от постоянного изгибающего момента).

3. При несимметричном загружении шарнирно-опертых элементов величину изгибающего момента М_м следует определять по формуле

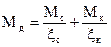, (32)

где М_с и М_к – изгибающие моменты в расчетном сечении элемента от симметричной и кососимметричной составляющих нагрузки;

x_с и x_к – коэффициенты, определяемые по формуле (30) при величинах гибкостей, соответствующих симметричной и кососимметричной формам продольного изгиба.

4. Для элементов переменного по высоте сечения площадь F_бр в формуле (30) следует принимать для максимального по высоте сечения, а коэффициент j следует умножать на коэффициент k_жN, принимаемый по табл. 1 прил. 4.

5. При отношении напряжений от изгиба к напряжениям от сжатия менее 0,1 сжато-изгибаемые элементы следует проверять также на устойчивость по формуле (6) без учета изгибающего момента.

4.18. Расчет на устойчивость плоской формы деформирования сжато-изгибаемых элементов следует производить по формуле

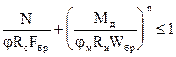, (33)

где F_бр – площадь брутто с максимальными размерами сечения элемента на участке l_p;

W_бр – см. п. 4.14;

n = 2 – для элементов без закрепления растянутой зоны из плоскости деформирования и n = 1 для элементов, имеющих такие закрепления;

j – коэффициент продольного изгиба, определяемый по формуле (8) для гибкости участка элемента расчетной длиной l_p из плоскости деформирования;

j_м – коэффициент, определяемый по формуле (23).

При наличии в элементе на участке l_p закреплений из плоскости деформирования со стороны растянутой от момента М кромки коэффициент j_м следует умножать на коэффициент k_пМ, определяемый по формуле (24), а коэффициент j – на коэффициент k_пN по формуле

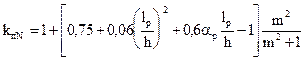, (34)

где a_p, l_p, h и m – см. п. 4.14.

При расчете элементов переменного по высоте сечения, не име­ю­щих закреплений из плоскости по растянутой от момента М кромке, или при m < 4 коэффициенты j и j_М, определяемые по формулам (8) и (23), следует дополнительно умножать соответственно на коэффициенты k_жN и k_жМ, приведенные в табл. 1 и 2 прил. 4.

При m ³ 4 k_жN = k_жМ = 1.

4.19. В составных сжато-изгибаемых элементах следует проверять устойчивость наиболее напряженной ветви, если расчетная длина ее превышает семь толщин ветви, по формуле

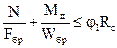, (35)

где j₁ – коэффициент продольного изгиба для отдельной ветви, вычисленный по ее расчетной длине l₁ (см. п. 4.6);

F_бр, W_бр – площадь и момент сопротивления брутто поперечного сечения элемента.

Устойчивость сжато-изгибаемого составного элемента из плоскости изгиба следует проверять по формуле (6) без учета изгибающего момента.

4.20. Количество срезов связей n_с, равномерно расставленных в каждом шве сжато-изгибаемого составного элемента на участке с однозначной эпюрой поперечных сил при приложении сжимающей силы по всему сечению, должно удовлетворять условию

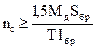, (36)

где S_бр – статический момент брутто сдвигаемой части поперечного сечения относительно нейтральной оси;

I_бр – момент инерции брутто поперечного сечения элемента;

Т – расчетная несущая способность одной связи в данном шве;

М_д – изгибающий момент, определяемый по п. 4.17.