Множество операций
Логические операции (а, по сути, логические функции) могут быть заданы на естественном языке, аналитически (булевыми выражениями), в виде таблиц, которые называются таблицами истинности, условными графическими обозначениями (схемное представление) и в виде моделей. Именно в такой последовательности будут даваться определения основных логических операций.
Операция «И»
Операция «И» (AND) (не путать с более известной в Росси и странах СНГ «Операцией «Ы»»!) по-другому называется конъюнкция, логическое умножение, «все или ничего», min(X1X0).
Задание на естественном языке: конъюнкция X1 и X0 истинна тогда и только тогда, когда истинно X1 и истинно X0.
Задание в аналитическом виде:
F=X1·X0=X1X0=X1&X0=X1∩X0= X1LX0.
В отличие от обычной алгебры, это произносится не как «X1 умножить на X0», а как «X1 и X2». Обычно человеку автоматически трудно перейти на правильное произношение, и требуются специальные усилия и тренировка, чтобы окружающие (в том числе и преподаватели) поняли, что Вы знаете, что такое булева алгебра.
Кстати, символ & называется «амперсанд».
Задание в виде таблицы истинности (truth table):
| X1 | X0 | F=X1X0 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Здесь уместно изложить принципы, по которым строится любая таблица истинности, поскольку именно эта таблица (по-другому называемая таблицей переключений, или комбинационной таблицей), является основным инструментом при проектировании цифровых устройств. Итак, таблица истинности состоит из левой и правой части (в вышеприведенной таблице разделение на эти части выделено жирной вертикальной чертой).
Слева располагается область аргументов. Количество столбцов в области аргументов определяется количеством используемых аргументов (мы рассматриваем простейший случай, поэтому у нас всего два аргумента и, соответственно, два столбца). Количество строк в таблице истинности определяется числом возможных значений комбинаций аргументов. Чтобы не пропустить какие-либо комбинации, рекомендуется в области аргументов просто записывать последовательность двоичных чисел, разрядность которых совпадает с количеством аргументов. Надеюсь, что подавляющее большинство, еще не забыло, что такое двоичная система счисления.
В правой области (области функции) записываются значения 0 или 1, которые будет принимать функция (операция) для комбинации значений аргументов в данной строке. Собственно значение функции (операции) в каждой строке и определяет представляемую операцию или функцию алгебры логики.
Графические условные обозначения устройства, выполняющего операцию И, приведены на рисунке 9.2. Такие устройства принято называть вентилями или логическими вентилями (gate или logical gate соответственно). Также принято в названии указывать количество входов (аргументов). Например, приведенные на рисунке 9.2 вентили называют 2И. В принципе существуют вентили с большим числом входов: 3И, 4И и 8И.
 |
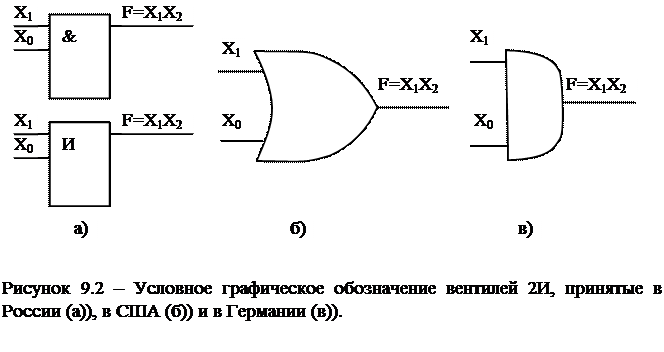И, наконец, на рисунке 9.3 показана электромеханическая модель операции И.
Отметим, что все вышесказанное для операции AND с двумя аргументами, может быть перенесено на операцию AND с произвольным количеством аргументов. Предлагается для закрепления материала воспроизвести все представления для операции AND с четырьмя аргументами.
Операция «ИЛИ»
Операция «ИЛИ» (OR) имеет также называния дизъюнкция, логическое сложение, «что-нибудь или всё», max(X1X0).
Задание на естественном языке: дизъюнкция X1 OR X0 истинна тогда и только тогда, когда хотя бы один из X1 и X0 имеет значение истина.
Задание в аналитическом виде:
F=X1+X0=X1UX0=X1wX0= X1#X0.
Это произносится не как «X1 плюс X0», а как «X1 или X2».
Задание в виде таблицы истинности (truth table):
| X1 | X0 | F=X1+X0 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Графические условные обозначения устройства, выполняющего операцию дизъюнкции, приведены на рисунке 9.4.
 | ||||||||||||
 |  | |||||||||||
|
| |||||||||||
| ||||||||||||
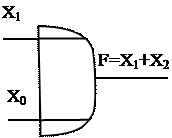На рисунке 9.5 приведен электромеханический аналог операции ИЛИ.
Здесь также полезно распространить полученные сведения на операцию дизъюнкции от четырех аргументов.
Для операций конъюнкции и дизъюнкции можно провести и другие (любые) аналогии. Например – сантехнические: «Вода появится в ванной через душ, если будет открыт или кран с холодной водой или кран с горячей водой и переключатель на душ».
Операция «НЕ»
Операция «НЕ» (NOT) имеет также такие названия: инверсия, отрицание.
Задание на естественном языке: НЕ X истинно тогда и только тогда, когда X имеет значение ложь.
Задание в аналитическом виде:
F=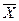 
=ØX=X`.
Это произносится как «не X».
Задание в виде таблицы истинности:
| X0 | F=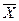
|
| 0 | 1 |
| 1 | 0 |
Несмотря на то, что по аналитической форме представления эта операция проще ранее рассмотренных, мне неизвестна простой электромеханический аналог операции NOT. На рисунке 9.6 приведена одна из возможных электромеханических моделей операции НЕ.
И в заключение, попробуйте распространить знания об операции NOT на несколько аргументов :).
Далее переходим к множеству постулатов.
