8 Сложение и вычитание в обратном и дополнительном кодах
Введение обратного и дополнительного кода позволило избавиться от операции вычитания. С использованием этих кодов операция вычитания сводится к операции сложения уменьшаемого и вычитаемого, причем вычитание представлено в обратном или дополнительном коде. Другими словами, операция D=A-B сводится к операции D=A+(-B), где B должно быть записано в обратном или дополнительном коде. Это достаточно сильный ход, позволяющий всю двоичную арифметику свести к сложению и сдвигам. Если Вы вернетесь к рассмотренным выше разделам, то вспомните, что умножение и деление было реализовано через сложение, сдвиги и вычитание.
Далее разделы будут содержать в заголовках слова «сложение и вычитание», но Вы уже понимаете, что на самом деле речь будет идти только о сложении
8.1 Сложение и вычитание в двоичном дополнительном коде
Суммирование ведется как обычно в двоичной системе, включая знаковые разряды, возможный перенос из старшего разряда отбрасывается. Правильный результат получится, если значение суммы не выходит за пределы диапазона представления чисел с заданной разрядностью для дополнительного кода. Как Вы помните, этот диапазон Вы ранее нашли самостоятельно :-). Если же сумма выходит за пределы этого диапазона, то говорят, что возникает переполнение (OVR - overflow).
Примеры:
4 – 9 = 4 + (-9) -5-6=(-5)+(-6)
[+4]Доп=0,0100 [+5]Доп=0,0101
[+9]Доп=0,1001 [+6]Доп=0,0110
[ -9]Доп=1,0111 [ -5]Доп=1,1011
[ -6]Доп=1,1010
 | |||||
 |  | ||||
+0,0100 +1,1011
1,0111 1,1010
1,1011 1,0101
Во втором примере перенос из знакового разряда (он изображен длинной стрелкой) в соответствии с правилом игнорируется.
Возникает вопрос – а как проверить правильность вычислений? Нужно контролировать два параметра – правильность знака и значение величинной части. По знакам вроде все нормально – результат и в первом примере и во втором примере должен получиться отрицательным, мы и имеем в знаковых разрядах по единице. А вот величинную часть «на глазок» оценить трудно (вот бы где пригодился прямой код, но в нем не так удобно производить вычисления).
Для проверки правильности значения величинной части при отрицательном результате нужно еще раз произвести преобразование, которое мы делали, когда получали отрицательное число в дополнительном коде. Здесь удобно использовать правило просмотра справа, тогда имеем:
1,1011→0,0101B=+510 1,0101→0,1011=+1110.
Как видно, результат по абсолютной величине получился правильный, а что он правильный по знаку мы уже убедились ранее.
8.2 Сложение и вычитание в двоичном обратном коде
Суммирование ведется как обычно в двоичной системе, включая знаковые разряды, возможный перенос из старшего разряда циклически прибавляется к младшему значащему разряду суммы. Правильный результат получится, если значение суммы не выходит за пределы диапазона представления чисел с заданной разрядностью для обратного кода. :-). Если же сумма выходит за пределы этого диапазона, то говорят, что возникает переполнение (OVR - OVeRflow). Операции в обратном двоичном коде применяются гораздо реже, но для обучения это очень полезная вещь.
Рассмотрим примеры.
4 – 9 = 4 + (-9) -5-6=(-5)+(-6)
[+4]Обр=0,0100 [+5]Обр=0,0101
[+9]Обр=0,1001 [+6]Обр=0,0110
[ -9]Обр=1,0110 [ -5]Обр=1,1010
[ -6]Обр=1,1001
| | |||
 | |||
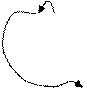+0,0100 +1,1010
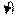1,0110 1,1001
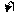1,1010 + 1,0011
1
1,0100
Длинная стрелка переноса означает «перенос из старшего разряда циклически прибавляется к младшему значащему разряду суммы». Проверку также осуществим проверкой знакового разряда и величинной части. Со знаковым разрядом все в порядке – оба числа получились отрицательными. Для проверки величинной части осуществим обратное преобразование (для обратного кода – проинвертируем все разряды, включая знаковый). Получим:
1,1010→0,0101B=+510 1,0100→0,1011=+1110.
Как видно, результат получен правильно.
8.3 Переполнение в двоичном дополнительном и обратном кодах
Чтобы разобраться с фразой «если значение суммы не выходит за пределы диапазона представления чисел с заданной разрядностью для данного кода», рассмотрим еще два примера.
10+10=20 (-10)+(-10)=(-20)
[+10]Доп=0,1010 [+10]Доп=0,1010
[ -10]Доп=1,0110
 | |||||||
 | |||||||
 | |||||||
 | |||||||
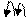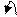+0,1010 +1,0110
0,1010 1,0110
1,0100 10,1100
С точки зрения двоичной арифметики, все вроде выглядит вполне нормально. Однако проверка на знак сразу дает сбой: в первом примере при сложении двух положительных чисел получается отрицательное, а во втором примере – при сложении двух отрицательных чисел в сумме получается положительное число. В принципе этими критериями можно пользоваться при определении факта переполнения. Однако, если Вы подумаете, как этот тест реализовать в микропроцессоре аппаратно, чтобы можно было выявить признак OVR, это может оказаться не совсем тривиально. Поэтому мы будем пользоваться другим определением, которое может быть не так очевидно, но совершенно верно, в чем Вы можете убедиться, проанализировав приведенные выше примеры. Итак,
|
Легко догадаться, что если правило выделено столь явно, то его нужно вызубрить наизусть.
А что нужно делать, если возникло переполнение? А нужно вернуться к исходным положительным числам, увеличить их разрядность и вновь выполнить действия. Нам в примерах обычно достаточно увеличить разрядность на один разряд, а микропроцессорам (а, точнее, программистам) приходится увеличивать разрядность числа на одно слово. Это в свою очередь приводит к увеличению занимаемого объема памяти, снижению быстродействия и т.д., поэтому заранее никто не берет разрядность с «запасом». А вот если микропроцессор скажет, что есть OVR, то в этом случае и нужно увеличить разрядность чисел.
Давайте последуем этому совету и переделаем последние примеры.
10+10=20 (-10)+(-10)=(-20)
[+10]Доп=0,01010 [+10]Доп=0,01010
[ -10]Доп=1,10110
 | |||||||
 | |||||||
 | |||||||
 | |||||||
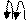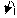+0,01010 +1,10110
0,01010 1,10110
0,10100 1,01100
В последнем случае перенос из знакового разряда, в соответствии с правилами, игнорируется. Если Вы проверите эти ответы, то не должны не увидеть никаких подвохов. Те же самые правила нужно применять при возникновении переполнения в случае вычислений с использованием обратного кода.
Изучение материала, который начинается с раздела «Представление двоичных чисел со знаком», совершенно необходимо для успешного выполнения домашнего задания и контрольной работы по третьему модулю.
На этом я заканчиваю тяжелый труд написания конспекта первых 2-3 лекций, которые читались «вживую» в дореформенный период высшего образования в России и СССР. Торжественно заявляю, что здесь изложена правда, правда и только правда.
Однако первый опыт чтения лекций с учетом вышеприведенного текста показал, что времени на «живых» лекциях все равно не хватает, поэтому тяжелый труд был продолжен…
9 Основные понятия алгебры логики
Математической основой цифровой техники служит булева алгебра (Boolean algebra), иногда называемая также алгеброй логики и предложенная в 1854 году Джорджем Булем. (1815 – 1864) для анализа человеческих рассуждений. По-другому булеву алгебру называют «исчисление высказываний», и оно входит в начальный раздел математической логики. Кстати, родился Джордж Буль 2 ноября 1815 года, а в этот же день, 2 ноября, но 1902 года, родился Сергей Алексеевич Лебедев – академик, Герой социалистического труда, лауреат Ленинской и Государственной премий, основоположник советской вычислительной техники, разработчик легендарного компьютера БЭСМ-6.
Дать определение основам булевой алгебры можно по-разному. Вот, например, как это делается в японских университетах [4]:
«Булева алгебра может быть определена как алгебраическая система, удовлетворяющая следующим постулатам.
Определение. Если для множества В = {a,b,c,…} и двух типов операторов + и · (логическая сумма и логическое произведение) справедливы четыре следующие соотношения, то такая система называется булевой алгеброй:
1) a+b=b+a, a·b=b·a для любых a,bÎB (коммутативность);
2) a+(b·c)=(a+b) (a+c), a·(b+c)=(a·b)+(a·c) для любых a,bÎB (дистрибутивность);
3) найдутся 1ÎB и 0 ÎB, такие, что a+0=a, a·1=a для любого aÎB (единичные элементы);
4) найдется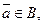 
такой, что 
, 
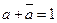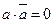для любого aÎB (дополнение).»
И это все!
Для тех, кто еще не понял, что такое булева алгебра, я позволю себе остановиться несколько подробнее, без японской лаконичности.
В общем случае общая математическая система определяется множеством элементов, множеством операций и множеством постулатов.
Множество элементов
В булевой алгебре существует 2 (всего два!) элемента, которые иногда называют ее константами и обозначают 0 и 1, для отличия от цифр их называют «логический 0» и «логическая 1». Считается обычно, что 1 соответствует выполнению какого-либо условия, высказывания или соответствует состоянию «истина» («truth»), а логический 0 – невыполнению условия, высказывания, состоянию «ложь» («false»). В качестве состояний «истина» и «ложь» могут быть использованы и уровни напряжения.
Говорят, что булевы переменные удовлетворяют условию «исключенного третьего», т.е.
x = 0 если х ≠ 1,
x = 1 если х ≠ 0,
в общем, или 0, или 1 – третьего не дано.
Состояния «истина» и «ложь» могут быть представлены в виде электромеханического (электрического) аналога (рисунок 9.1).