7 Представление двоичных чисел со знаком
Жить становится лучше, жить становится веселее, если можно оперировать с отрицательными числами. Сама по себе двоичная система счисления такой возможности не предоставляет. Поэтому для возможности работы с отрицательными числами в двоичной системе вводят коды: прямой, обратный и дополнительный.
В качестве образца для подражания давайте, как обычно, возьмем десятичную систему счисления и вспомним, как в ней представляются числа со знаком. В десятичной системе счисления знак отмечается специальным символом (+ или -), располагаемым слева от числа. Причем общепринято, что отсутствие специального знака (слева «ничего нет»).
Если это переносить в двоичную систему счисления то единственная сложность, которая может встретиться – это введение специального символа. Ведь в двоичной системе счисления не может существовать ничего кроме 0 и 1. Поэтому единственный выход – использовать 0 или 1 для обозначения знака числа. Совершенно очевидно, что 0 или 1, обозначающие знак, должны располагаться слева, перед собственно числом (или, как говорят, величинной частью). И этот разряд, где располагается 0 или 1, обозначающие знак числа, логично называть знаковым разрядом. Осталось выбрать, как следует отмечать положительное число и как отмечать отрицательное. Представляется, что аналогом «ничего нет» скорее должен выступать 0, чем 1. Поэтому и будем считать, что 0 слева обозначает положительное число, а 1 – отрицательное.
Таким образом, для представления чисел со знаком в прямом, обратном и дополнительном кодах старший разряд числа (n-1-ый разряд) трактуется как знаковый разряд. Если в знаковом разряде находится 0, то число считается положительным, а если в знаковом разряде находится 1, то число считается отрицательным. Оставшиеся разряды служат для записи величинной части числа.
Для того чтобы подчеркнуть, что используется число со знаком принято знаковый разряд отделять запятой от величиной части. Естественно, в микропроцессорах при представлении отрицательных чисел никакой запятой нет, эта запись используется только людьми, которые хотят показать, что они имеют в виду именно числа со знаком. Примеры записи двоичных чисел со знаком:
0,100101001 0,00100101 1,100101001 1,00100101
Далее будут даны определения чисел со знаком в прямом, обратном и дополнительном кодах. Чтобы их отличать друг от друга следует использовать специальную форму записи. В этой записи исходное десятичное число с явным указанием знака записывается в квадратных скобках, справа от которых подстрочным шрифтом обозначается вид кода:
[+10]Пр =0,01010 [-10]Пр =1,01010
[+10]Обр=0,01010 [-10]Обр=1,01010
[+10]Доп=0,01010 [-10]Доп=1,01010
7.1 Представление двоичных чисел со знаком в прямом коде
Для представления чисел во всех рассматриваемых здесь кодах существует два правило. Одно правило используется для представления положительных чисел, другое – для представления отрицательных чисел.
Чтобы представить положительное двоичное число в прямом коде следует в знаковый разряд записать 0, а в величинную часть – само двоичное число (надеюсь, Вы помните, что уже выучили наизусть двоичные числа от 0 до 16?). Пример:
[+1]Пр=0,0000001 [+9]Пр=0,01001 [+13]Пр=0,1101
Чтобы представить отрицательное двоичное число в прямом коде следует в знаковый разряд записать 1, а в величинную часть – само двоичное число. Пример:
[-1]Пр=1,0000001 [-9]Пр=1,01001 [-13]Пр=1,1101
Бросается в глаза, что в прямом коде очень легко записывать и понимать отрицательные числа – не надо делать никаких вычислений и преобразований. Это главное (и, к сожалению, единственное) достоинство прямого кода. Действительно, прямой код применяется для удобства чтения отрицательных чисел человеком, вычисления в нем не производятся.
Формально на этом можно было бы и закончить, однако грамотный специалист, кроме знаний о том, как представить число в данном коде должен уметь делать следующее:
1. Представлять графически зависимость чисел в коде от величины двоичного числа.
2. Уметь записать аналитическое выражение, по которому можно было бы вычислить значение числа, представленного в данном коде.
3. Уметь определять диапазон чисел, которые могут быть представлены в заданном числе разрядов в данном коде.
В силу простоты прямого кода эти вопросы для этого кода будут рассмотрены подробно, а для остальных кодов Вы это сделаете самостоятельно.
Ответ на первый пункт заключается в умении построить график, по оси x которого будут откладываться двоичные числа, а по оси y – числа со знаком в изучаемом коде. Результат такого построения для прямого кода в случае четырех разрядов двоичных чисел показан на рисунке 1. В частности, из рисунка следует, что у чисел в прямом коде существуют два нуля: это так называемый +0 (ему соответствует число 0,000) и так называемый -0 (ему соответствует число 1,000).
Записать аналитическое выражение для прямого кода достаточно просто. Младшие (n-2) разряда (величинная часть) дают числовой эквивалент числа, который, как мы помним, находится с помощью формулы 4. (n-1) разряд определяет знак числа. Если этот разряд равен нулю, то число является положительным, а если этот разряд равен единице – то число отрицательно. Все это легко объединяется в следующей формуле:
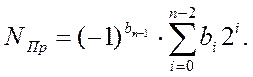
| (19) |
 |
Диапазон целых чисел, представляемых n разрядным прямым кодом можно найти из следующих соображений. Минимальное (отрицательное) число получится, когда в величинной части будут все единицы. Максимальное (положительное) число также получится, когда в величинной части будут все единицы. Следовательно, нужно найти, чему будет равно двоичное число, в котором в (n-2) разрядах записаны одни единицы. Для этого нужно в явном виде расписать формулу (5):
Nmax=1·2 n-2+1·2 n-3+…+1·24+1·23+1·22+1·21+1·20. (20)
Очевидно, что Nmax представляет собой сумму геометрической прогрессии, в которой первый член равен 1, а множитель – 2. Сумма:
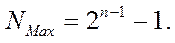
| (21) |
В результате диапазон чисел, представляемых в прямом коде числами в n разрядах запишется как
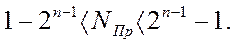
| (22) |
Теперь можно сказать, что представление двоичных чисел со знаком в прямом коде рассмотрено достаточно подробно.
7.2 Представление двоичных чисел со знаком в обратном коде
Прежде чем говорить о собственно двоичном обратном и дополнительном кодах, рассмотрим понятия обращения и дополнения. Дополнением называют сдвиг по числовой оси исходного числа на некоторую константу. Другими словами, дополнением К числа N до числа M называют величину K=M-N, где M – число, на единицу большее максимально достижимого числа для разрядности числа N. Например, есть десятичное число 2003. Максимально возможное десятичное число для этой разрядности есть число 9999. Тогда числом, превосходящим его на 1, будет число 10 000. И дополнением числа 2003 будет число 10 000 – 2003 = 7997.
Обращением числа N называют величину K=M-N-1=(M-1)-N, где M определено выше.
Рассмотрим, как можно получить обращение числа в двоичной системе счисления. Проверим это на простом примере. Возьмем двоичное число N=1101B и найдем его обращение. Соответствующим числом M должно быть число 10000B, тогда M-1:
 |
_10000
1111
1111
Найдем далее обращение (M-1)-N:
_1111
1101
0010
Если мы сравним исходное число 1101B и его обращение 0010B, то мы увидим, что они отличаются друг от друга только обращением всех разрядов!
Таким образом, имеется основание сформулировать следующее правило: для получения обращения двоичного числа достаточно проинвертировать все его разряды.
Ну, а теперь собственно определения записи чисел со знаком в обратном двоичном коде.
Чтобы представить положительное двоичное число в обратном коде следует в знаковый разряд записать 0, а в величинную часть – само двоичное число. Пример:
[+1]Обр=0,0000001 [+9]Обр=0,01001 [+13]Обр=0,1101
Чтобы представить отрицательное двоичное число в обратном коде следует взять соответствующее положительное число и проинвертировать все его разряды, включая знаковый. Пример:
[-1]Обр=1,1111110 [-9]Обр=1,10110 [-13]Обр=1,0010
Видно, что для записи отрицательных чисел в обратном коде никаких арифметических действий выполнять не нужно.
Ну вот, Вам теперь осталось попытаться приблизиться к грамотным специалистом и выполнить три задания, сформулированные в предыдущем разделе. Для записи этих результатов отводится место ниже.
7.3 Представление двоичных чисел со знаком в дополнительном коде
Чтобы представить положительное двоичное число в прямом коде следует в знаковый разряд записать 0, а в величинную часть – само двоичное число. Пример:
[+1]Доп=0,0000001 [+9]Доп=0,01001 [+13]Доп=0,1101
(Интересно, а сколько отличий Вы нашли в правилах записи положительных чисел в прямом, обратном и дополнительном двоичных кодах?)
Чтобы представить отрицательное двоичное число в дополнительном коде следует взять соответствующее отрицательное число в обратном коде и прибавить к нему единицу. Пример:
[-1]Обр=+1,1111110 [-9]Обр=+1,10110 [-13]Обр=+1,0010
1 1 1
[-1]Доп = 1,1111111 [-9]Доп= 1,10111 [-13]Доп= 1,0011
Здесь возможен случай, когда придется производить вычисления (в примерах таких случаев нет, но если Вы в качестве исходных чисел возьмете четные числа, то – в общем, возьмите и попробуйте). Поэтому на практике удобно применять другое правило, которое (почти всегда) дает правильный результат. Итак, правило два: берется соответствующее положительное число и просматривается справа налево (от младшего значащего разряда к старшему значащему разряду) до тех пор, пока не встретится единица. Эта единица оставляется без изменений, а остальные разряды, включая знаковый, инвертируются.
Правило, действительно, удобное, но не забывайте, что изредка могут возникать проблемы.
Отметим, что в микропроцессорах вычисления для чисел со знаком всегда ведутся с использованием дополнительного кода.
Осталось найти ответы на три основных самостоятельных вопроса по кодам. Место оставлено.








