3 Преобразование чисел из одной системы счисления в другую
При необходимости перевода числа из одной системы счисления в другую следует сразу же выделить два случая, принципиально отличающихся друг от друга. Первый случай – перевод из произвольной системы счисления в десятичную систему – это достаточно простая задача. Второй случай – перевод из десятичной системы в произвольную систему счисления. Эта задача посложнее и ее нужно решать в рамках правил перевода чисел из произвольной системы счисления в произвольную. Но для начала, говорят, лучше решить задачку попроще.
3.1 Перевод числа в десятичную систему счисления
Этот перевод легко осуществить простым вычислением полинома (4).
Алгоритм:
1. Записываем число в виде полинома
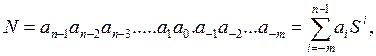
| (8) |
где S – основание системы счисления в десятичное системе счисления. Для двоичной, восьмеричной и шестнадцатеричной систем счисления это 2, 8 и 16 соответственно. Для шестнадцатеричной системы счисления вместо цифр A, B, C, D, E, F нужно подставлять их десятичные эквиваленты.
2. Вычисляем значение полинома, пользуясь десятичной арифметикой (которая нам, надо полагать, хорошо знакома).
Пример:
| 1D0.4H=1∙162+13∙161+0∙160+4∙16-1=256+208+0+0.25=464.25 | (9) |
Обратите внимание, что те, кто забыл со школы, чему равно 162, но занимаются сейчас, легко восполнят школьный пробел, заменив это число на 28.
3.2 Перевод числа из произвольной системы счисления в произвольную систему счисления
Для начала упомянем, что существует некоторый промежуточный способ перевода из десятичной системы в произвольную, называемый табличным. Наиболее активным предлагается ознакомиться с этим способом самостоятельно.
Мы же сконцентрируем свое внимание на универсальном способе перевода. Попробуем сформулировать задачу – что у нас есть, и чего мы хотим получить (дано – найти – ну все как в школе! А может быть, там все правильно учили?). Итак, то, что у нас есть число N в произвольной системе счисления с основанием S, означает, что мы имеем: во-первых, краткую форму записи этого числа, в которой нам заданы все цифры ai, во-вторых, мы знаем, что за краткой формой числа скрывается некий числовой эквивалент, вычисляемый по формуле (4). Это еще раз представлено формулой
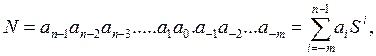
| (10) |
Что нам нужно найти? Нам нужно найти, как этот число (числовой эквивалент не зависит от системы счисления и формы представления числа) будет представлено в новой системе счисления новыми цифрами ai` и новым основанием S`, т. е. найти представление (11):
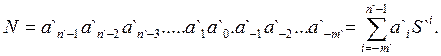
| (11) |
А фактически, нам нужно найти совокупность ai` , поскольку S` нам задано. Или другими словами, нужно найти значения ai` , удовлетворяющие уравнению (11)- т.е. как-то решить это уравнение.
Давайте рассмотрим отдельно перевод целой части числа и дробной части числа.
3.2.1 Перевод целой части числа
Кто-то, несомненно, талантливый человек, предложил такой способ: поделить N/ S`. Давайте формально запишем результат деления (11) на S`:
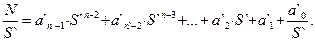
| (12) |
Здесь возможны 2 случая: если N< S`, то получится частное, меньше 1, т.е. отличен от 0 только коэффициент а`0 – тогда результат достигнут и нужно просто оставить а`0 - это тривиальный случай и он не интересен. Если N> S`, то должно получиться целое частное N1I (индекс I от слова Integer - целый) (13) и остаток (14), который не делится нацело:
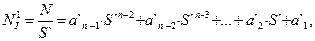
| (13) |
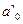
| (14) |
Остаток (14) получился, поскольку любая цифра всегда меньше основания системы счисления. Таким образом, нам удалось найти цифру младшего разряда в новой системе счисления.
Теперь если мы поделим N1 I на S` и снова выделим целое частное и остаток:
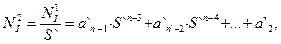
| (15) |
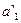
| (16) |
Таким образом, мы нашли следующую цифру числа в новой системе счисления.
Эту процедуру мы можем проделать какое-то число раз, пока не найдем все a` i. Очевидно, что для этого потребуется n-1 шаг. После этого, выписав все остатки так, что первый находится справа, а последний слева и, приписав к нему слева частное, меньшее S` (последнее частное) мы получим число N в системе счисления с основанием S`. Причем здесь потребуется конечное число шагов.
3.2.2 Перевод дробной части числа
Поскольку дробная часть (кстати, на английском, дробь - это Fraction) является некой противоположностью по отношению к целой части, то для перевода дробной части надо применить нечто противоположное. Относительно деления противоположным можно считать умножение. Действительно, давайте, применим операцию умножения на S` по отношению к дробной части. В результате получаем:
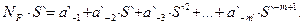
| (17) |
Анализируя полученное выражение, мы видим, что можно выделить целую часть a`-1 и дробную часть N1 F:
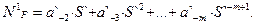
| (18) |
Целая часть a`-1 – это как раз то, что нам нужно – первая цифра дробной части!
Ну, а теперь, как часто говорят – легко сообразить – повторяя операцию умножения оставшейся дробной части на основание новой системы счисления мы будем получать следующие цифры дробной части числа в новой системе счисления. Однако, отметим, что, в отличие от перевода целой части числа, здесь не обязательно дело закончится конечным числом операций (хотя, кому-то может и повезти). Ведь существуют бесконечные дроби… И тут есть над чем подумать: будешь слишком много раз умножать – конкуренты обойдут, слишком мало – тоже, наверное, плохо! Свои мысли можно будет изложить в домашней работе и на экзамене.
3.2.3 Перевод смешанного числа
Тут, наверное, тоже легко сообразить, что нужно по отдельности перевести целую часть числа и дробную часть числа.
Ну, а теперь приведем полную формулировку правила перевода любого числа из одной произвольной системы счисления в другую произвольную систему счисления.
Для перевода целой части числа из одной позиционной системы с основанием системы счисления S в другую, с основанием S` (S` - основание новой системы) необходимо это число последовательно делить на S`, выписывая остатки до тех пор, пока не получится частное меньше S`. Число в новой системе запишется в виде остатков, первый остаток образует младший разряд, в старший разряд записывается последнее частное, меньшее основание новой системы. Деление выполняется в исходной системе, результат записывается цифрами новой системы.
Чтобы перевести правильную дробь из одной позиционной системы с основанием S в другую, с основанием S`, необходимо дробь последовательно умножать на S`, при этом умножаются только дробные части, а целые части, начиная с первой, являются цифрами дробного числа в новой системе счисления. Умножение выполняется в исходной системе, дробь записывается цифрами новой системы.
Рассмотрим такой пример: переведем число 37.625 из десятичной системы в десятичную.
Начнем с целой части. В соответствии с выведенным правилом будем 37 последовательно делить на 2:
37 | 2
2 18 | 2
17 18 9 | 2
16 0 8 4 | 2
1 1 4 2 | 2
0 2 1
0
В результате деления осталась 1 (самая правая). Она не делится на 2, и она образует старший значащий разряд (забыл, как это по английски?). Если теперь начиная с этой единицы выбирать все остатки (они выделены жирным шрифтом и курсивом) справа налево и записывать их в двоичное число слева направо получим:
1001012
Теперь переведем дробную часть.
0|.625 * 2
1|.25 * 2
0|.5 * 2
1|.0
Здесь по случайному стечению обстоятельств дробная часть быстро закончилась. Если теперь выписать целые части (они тоже выделены жирным шрифтом и курсивом), то мы получим дробную часть:
0.1012
Таким образом, имеем
37.62510 = 100101.1012
Настоятельно рекомендуется при переводе чисел запись вычислений производить в представленной здесь форме.
Еще раз отметим, что приведенные правила верны для переводов из любой позиционной системы счисления в любую. В том числе и из двоичной в десятичную. Давайте переведем, пользуясь этими правилами, число 1001012 в десятичную систему счисления. Единственное что нам может помешать, так это то, что мы пока не умеем выполнять арифметические действия в двоичной системе счисления (как Вы помните, вычисления должны производиться в исходной системе счисления). Однако есть подозрение, что деление столбиком, которым мы лихо пользуемся в десятичной системе счисления, должно работать в любой системе счисления (ведь десятичная система формально не имеет никаких особенностей перед другими системами счисления!). Придерживаясь рекомендуемой формы записи, получим:
100101 | 1010
1010 11
10001
1010
111
Записывая полученные остатки 11 и 111 в десятичной системе счисления, получим число 37. Некоторым может показаться, что мы зря вводили правило для перевода в десятичную систему счисления. Да, зря если Вам кажется, что делить столбиком в произвольной системе счисления (например, в двоичной, девятеричной и т.д.) удобнее, чем вычислять полином в десятичной системе счисления.
Для проверки полученных навыков можно попытаться перевести некоторое число из пятеричной системы счисления в семеричную. Тут, кстати, возникает вопрос: а как проверить правильность перевода? Я рад, если у кого-то этот вопрос возник еще ранее. Надо над этим подумать…
3.3 Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления и обратно
Запишем произвольное число в двоичной системе счисления в соответствии с (5):
N= + b828+ b727+ b626+ b525+ b424+ b323+ b222+ b121+ b020.+ b-12-1+ b-22-2+ b-32-3+ b-42-4+ b-52-5+ b-62-6+
Давайте теперь в этом выражении несколько сгруппируем члены по три (в триады)
N= + ( b828+ b727+ b626)+( b525+ b424+ b323)+( b222+ b121+ b020).+( b-12-1+ b-22-2+ b-32-3)+( b-42-4+ b-52-5+ b-62-6)+…
Теперь из каждой скобки вынесем по общему множителю
N= + (b822+b721+b620)26+(b522+b421+b320)23+(b222+b121+b020)20.
+( b-122+ b-221+ b-32-0)2-3+( b-422+ b-521+ b-620)2-6+…=
= + ( b822+ b721+ b620)(23)2+( b522+ b421+ b320)(23)1+( b222+ b121+ b020)(23)0.
+( b-122+ b-221+ b-32-0)(23)-1+( b-422+ b-521+ b-620)(23)-2+…=
= ( b822+ b721+ b620)82+( b522+ b421+ b320)81+( b222+ b121+ b020)80.
+(b-122+b-221+b-32-0)8-1+(b-422+b-521+b-620)8-2+…=
= + O282+ O181+ O080.+ O-18-1+ O-28-2+… (19)
Рассмотрим, что же скрывает под символом Oi. Это выражения вида (bi22+bi21+bi20), где bi принимает значения 0 или 1. Отсюда следует, что Oi может принимать значения 0, 1, 2, 3, 4, 5, 6, 7. Пусть теперь в меня бросят камень, если последняя строка в (19) – это не запись числа в восьмеричной системе счисления. Если у кого-то рука все же потянулась к камню, пусть лучше направит свою энергию на более внимательное прочтение этих страничек, а именно, пусть посмотрит на формулу (6). Вот так-то!
Для тех, кто так ничего и не понял, просто сформулируем правило:
Для перевода числа из двоичной системы счисления в восьмеричную систему счисления нужно, начиная от позиционной точки, разбить все двоичное число на триады. Недостающие слева и справа разряды следует дополнить нулями до получения полных триад. Заменив триады восьмеричными цифрами, получаем число в восьмеричной системе счисления.
Совершенно очевидно, что применимы и обратные преобразования - предлагается сформулировать правило перевода чисел из восьмеричной системы счисления в двоичную самостоятельно.
Кроме того, увидев, что ниже оставлено пустое место, и поглядев на заголовок данного раздела, каждый поймет, что также самостоятельно нужно провести аналогичные преобразования для обоснования правил перевода из двоичной системы счисления в шестнадцатеричную и обратно, и сформулировать эти правила.
Приятного Вам времяпровождения!
Зубрения этого текста с последующим пониманием должно хватить для успешного выполнения домашнего задания и контрольной работы по первому модулю РГР.








