2 Наиболее употребительные системы счисления
2.1 Двоичная система счисления
Но, как бы там ни было, в настоящее время в цифровой технике используется двоичная система счисления, и изучение различных систем счисления мы начнем именно с нее.
Двоичная система в качестве основания системы счисления использует 2. На английском языке это записывается как binery [΄bainэr:] - двойной, сдвоенный (это для тех, кто не учил английского языка – теперь они теряют этот ценный козырь «А я не учил английский язык»).
Для двоичной системы счисления формула (4) принимает вид:
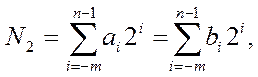
| (5) |
где ai=0,1, а применение bi вместо ai подчеркивает, что это двоичная система.
В двоичной системе каждый разряд называют битом (bit – это сокращение, образованное слиянием двух слов: binary и digit [didjit] цифра). На самом деле в транскрипции слова digit должен стоять другой символ, но я нашел, как это сделать в Word’е. Так вот, слово бит образуется как слияние первой буквы слова binery и двух последних букв слова digit (ну, или, если хотите, первых двух букв слова binery и последней буквы слова digit). Т.е. бит - это 0 или 1.
Для обозначения того, что число записано в двоичной системе счисления применяют приема. Первый состоит в применении подстрочного индекса 2: 10102. Но не все знают, как быстро перейти к подстрочным индексам (а, действительно, как?), а в печатающих машинках (если кто о таком слышал) это и сложно. Поэтому можно использовать в качестве обозначения букву B (надеюсь, большинство понимает, почему именно эта буква используется): 1010B.
Посмотрим, как можно построить числа в двоичной системе счисления.
Будем составлять последовательность натуральных двоичных чисел, пользуясь введенным выше правилом. Берём 0 – это и будет первое натуральное число в двоичной системе счисления. Для получения следующего числа прибавляем 1, получим 1. Итак, первые числа будут:
0, 1.
Чтобы получить следующее число, надо к единице прибавить еще одну единицу, получим число 2. Но цифры 2 не может быть в двоичной системе счисления, поэтому мы должны ввести следующий разряд и записать 10. Здесь произошел перенос из нулевого разряда в первый. Для перехода к следующему числу прибавляем 1, и получаем 11. Дальнейшее прибавление 1 приведет опять к тому, что в нулевом разряде должно получиться число 2, и возникает перенос в первый разряд, а в нулевом разряде запишем 0. Однако перенос в первый разряд приведет к появлению в первом разряде двойки, поскольку переносы прибавляются к значению, имеющемуся в разряде. Следовательно, здесь тоже должен возникнуть перенос, но уже во второй разряд, а в первом разряде следует записать 0 и результатом будет число 100. Чтобы все выглядело грамотно, эту последовательность нужно записывать в таком виде:
000B 001B 010B 011B 100B …. или 0002 0012 0102 0112 1002 …
Ну, а дальше каждый напишет сам, я лишь позабочусь, чтобы на этой (или на следующей) страничке оказалось для этого место.
Говоря о двоичных числах, пользуются понятием наименьший значащий бит (самый младший двоичный разряд, в более широком смысле принята отечественная аббревиатура МЗР – младший значащий разряд) и наибольший значащий бит (самый старший значащий разряд, соответственная аббревиатура СЗР – старший значащий разряд). На английском языке соответствующие аббревиатуры применяют к двоичной системы и выглядят они следующим образом: LSB – Low Significant Bit и MSB - Most Significant Bit. LSB имеет наименьший вес, MSB - наибольший вес.
Сам по себе бит несет слишком мало информации, поэтому в двоичной системе счисления применяются комплексы, состоящие из более чем одного бита. Группа из n двоичных разрядов, используемая для представления того или иного символа, называется байтом (byte). Вначале использовались 5 и 6 разрядные байты, но они оказались малыми. Например, с помощью 5 разрядного байта можно кодировать 32 комбинации, 6 разрядного -64, в то время как в русском алфавите 33 буквы, в латинском 26, + 9 десятичных цифр, + спецзнаки. Поэтому желательно минимум 7 разрядов, а лучше 8 разрядов. Поэтому, в настоящее время байтом называется восьмиразрядное бинарное слово. (Хотя иногда под байтом понимают собственный байт + контрольный разряд - т.е. 9 разрядное слово). В байте могут помещаться числа от 0 до 255, т. е. двести пятьдесят шесть комбинаций.
На самом деле между битом и байтом есть еще группа из четырех бит, называемая тетрадой, нибблом, слогом или полубайтом.
Таким образом, реально используемой минимальной группой двоичных разрядов является тетрада – 4 двоичных разрядов. Именно поэтому разрядность практически всех микропроцессоров кратна 4: 4, 8, 12, 16, 32 - разрядные микропроцессоры.
Существует более крупная, чем байт, единица - машинное слово, разрядность машинного слова определяется разрядностью машины. Обычно машинное слово 2 байтам, но иногда считают, что слово равно четырем байтам. Для повышения точности вычислений в машинах могут использоваться слова удвоенной длины. Обычное машинное слово, состоящее из шестнадцати разрядов, может содержать числа от 0 до 65535 – всего 65536 чисел.
Также используется единица в 1 Кило (байт или бит), равная 210=1024. Следующей из используемых единиц является 1 Мега, составляющая 1 Кило*1 Кило = 220 = 210*210= 1048576. Также можно найти, чему равняется 1 Гига, но это читатель уже сделает самостоятельно.
Итожа, скажем, что нужно выучить наизусть двоичные числа от 0 до 15 и следующие степени числа 2: 28 и 216.
Недостатки двоичной системы счисления - непривычность и трудность анализа, связанная с большим количеством разрядов. Поэтому широко применяются системы счисления с основанием S, большим, чем 2, причем оказалось удобным брать S кратное степени 2.
2.2 Восьмеричная система счисления
Восьмеричная система (применялась в μЭВМ Э-60 (более известной в мире под названием PDP-11) при подготовке задач, в процессе программ, проверке работы машины и отладке программы).
На английском языке восьмеричная система записывается как octal [oktэl].
Уравнение (4) выглядит следующим образом:
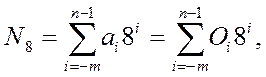
| (6) |
где ai - цифры 0 12 3 4 5 6 7, а буква O еще раз подчеркивает принадлежность к восьмеричной системе.
Обозначение восьмеричных чисел заключается в использовании подстрочного индекса 8 (10108) или в прибавлении справа от числа латинской буквы O (1010O). Однако в понедельник, с самого утра, в последней записи очень легко сделать ошибку. Поэтому, чтобы отличать нули от буквы O, нули следует писать перечеркнутыми (что-то вроде Ø, но «руками» это получается просто и непринужденно), а букву O – неперечеркнутой. Кстати, а как обозначаются восьмеричные числа в языке Си?
Пользуясь введенным выше правилом, напишите восьмеричные числа от 0 до 15 (для этого ниже оставлено пустое место).
По отношению к двоичной системе счисления числа в восьмеричной системе счисления выглядят более компактными, при этом, как покажем далее, переход от восьмеричной системы к двоичной и обратно осуществляется очень просто.
2.3 Шестнадцатеричная система счисления
Эта система наиболее широко используется в микропроцессорной технике. На английском языке она записывается как Hexadecimal.
Уравнение (4) для шестнадцатеричной системы счисления принимает вид
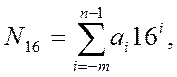
| (7) |
где ai - 0 12 3 4 5 6 7 8 9 A B C D E F (надо выучить наизусть!!!).
Для обозначения чисел в шестнадцатеричной системе, как легко догадаться, используется подстрочный индекс (101016) или буква H (h) (1010H, 1010h).
Использование шестнадцатеричной системы счисления позволяет компактно записывать числа, но, в отличие от восьмеричной системы счисления, при этом легко разбивать большие числа на байты и тетрады. Так же как и восьмеричная система счисления, шестнадцатеричная система позволяет легко переходить к двоичной и обратно.
Рассмотрим еще два представления чисел, часто встречающиеся на практике.
2.4 Двоично-десятичный код (код BCD – Binery Coded Decimal)
При отображении десятичных чисел в микропроцессорных системах и в некоторых вычислениях качестве промежуточной используют двоично-десятичный код. По другому его называют натуральным двоично-десятичным кодом, кодом 8-4-2-1 или котом BCD. В большинстве процессоров (в том числе и в процессорах семейства Pentium) присутствует специальных тип данных, поддерживающих код 8-4-2-1. Для Pentium это типы BCD Integer и Packed BCD. Смысл этого кода легче всего понять, если дословно перевести его английское название «Двоично кодированные десятичные (цифры)»
Двоично-десятичный код получается так: каждая десятичная цифра десятичного числа представляется в двоичном коде - для этого требуется 4 разряда - тетрада. Во избежание путаницы число битов в кодирующих группах должно быть строго фиксированным и всегда равным четырем, и при записи цифр 010 - 710 левые нули должны присутствовать. Многоразрядные десятичные числа в коде BCD представляются путем объединения (конкатенации) тетрад, кодирующих отдельные десятичные цифры.
Например число 2003 в коде BCD будет выглядеть так:
0010 0000 0000 0011
При записи, чтобы подчеркнуть, что осуществляется конкатенация, между тетрадами ставят визуализаторы пробела:
0010|_|0000|_|0000|_|0011
Если взять тетраду, и записать в каждый разряд, начиная со старшего, по единице, то получим такую последовательность тетрад:
1000 0100 0010 0001
Этим тетрадам соответствуют десятичные числа 8-4-2-1 (ведь Вы уже выучили наизусть двоичные числа от 0 до 15!). Может быть, это прояснит, почему этот код иногда и называют кодом 8-4-2-1.
Код 8421 страдает избыточностью, так как максимальная десятичная цифра 9 кодируется тетрадой 1001, а остальные комбинации (которых в тетраде всего может быть 16) не нужны. При выполнении операций в десятичном коде можно получить результат, включающий "цифру" от 1010 до 1510 - подобные, непредусмотренные этим кодом цифры, называют псевдотетрадами. Для исправления записи псевдотетрод их следует или уменьшить на 1010 = 10102 и следующий по старшинству разряд увеличить на 1 или добавить 610 - 1102 (что также автоматически приведет к появлению 1 переноса). Такая операция называется коррекцией псевдотетрад.
Двоично-десятичное кодирование очень удобно при выводе чисел в десятичной форме на цифровых индикаторах (вакуумных, газоразрядных), для этого разработаны специальные простые интегральные схемы - например в вольтметрах - выход цифр информации в 8421.
2.5 Код Грея
Код Грея (рефлексный код) - он не используется для вычисления и преобразования числовой информации, в отличие от вышерассмотренных кодов. Его область применения - шифрация углов поворотов механических валов - связана со следующей особенностью: всегда при переходе от числа к числу происходит изменение только одного разряда.
Например, в некотором цифровом устройстве, использующем двоичную систему счисления, должен произойти переход от 01112 к 10002. Поскольку мгновенно ничего не происходит, это переход может происходить разными путями. Возможно, при переходе сначала четвертый разряд установится в 1, тогда на какой-то миг будет присутствовать число 11112. Потом по очереди разряды 0-3 будут переходить в 0. В этом случае в какие-то моменты времени будут существовать числа 11102 и 11002. Но, возможно, в этом устройстве, при переходе от 01112 к 10002 сначала по очереди (а, может быть, и в беспорядке) будут сброшены в 0 разряды 0-3, а потом в 1 будет установлен разряд 4. В таком случае в какие-то моменты времени будут присутствовать числа 01102, 01002, 00002и 10002. И если другой прибор будет с большой частотой производить опрос состояний рассматриваемого прибора, то он будет наблюдать вовсе не переход сразу от 01112 к 10002 а совершенно другие переходы. Вот чтобы избежать таких ситуаций, и применяется код Грея.
Правило для получения кода Грея [3]: начинать нужно с нулевого состояния, а затем для получения каждого следующего нужно найти самый младший разряд, изменение которого приводит к образованию нового состояния, и взять его инверсное значение. Арифметические действия производить с кодом Грея нельзя, поэтому для вычислений его нужно переводить в двоичную систему счисления. А теперь можно и потренироваться в записи чисел в коде Грея от 0 до 15 и далее. Место уже оставлено. Если не получается, смотри книгу [3].
Для закрепления полученных результатов требуется (обратите внимание – не рекомендуется, не предлагается, а именно требуется) как минимум заполнить следующую таблицу:
Таблица 1. Представление чисел в различных видах
| Десятичная система счисления | Двоичная система счисления | Восьмеричная система счисления | Шестнадцатеричная система счисления | BCD | Код Грея |
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 | |||||
| 11 | |||||
| 12 | |||||
| 13 | |||||
| 14 | |||||
| 15 |
Ну, и самое главное, теперь эту таблицу (за исключением кода Грея) нужно вызубрить наизусть, как таблицу умножение.








