1 Позиционные системы счисления
Зачем нужны другие системы счисления? (Этот вопрос подразумевает, что читающий эти фрагменты лекций, знает достаточно хорошо хотя бы одну систему счисления.)
Ну, и зачем мы должны изучать другие системы? И нужно ли их изучать? Вроде, человеку (нормальному) достаточно десяти пальцев на двух руках, из чего, как можно предположить, и проистекает всем привычная десятичная система счисления.
Частичный ответ может заключаться в том, что после изучения вопросов, связанных с системами счисления, мы будем готовы к тому, чтобы не удивляемся таким записям:
1 + 1 = 2 1 + 1 = 1 7 + 6 = 15 (эта запись неполная),
1 + 1 = 10 7 + 6 = D ( здесь тоже нужно кое-что дополнить).
Итак, приступим. (Хотя следует отметить, что большую часть материала этого раздела студенты должны были проходить в школе, в 5 классе. Но, иногда, после разговоров с некоторыми студентами возникает сомнение в верности этого, казалось бы, очевидного постулата). Система счисления (СС) - совокупность правил для записи действительных чисел с помощью цифровых знаков.
Различают непозиционные и позиционные СС.
В непозиционной СС количественный эквивалент любой цифры не зависит от места цифры в ряду других.
Пример: запись палочками-крестиками (одна палочка – один мамонт, другая палочка – все равно один мамонт), счет на пальцах. Наибольшее развитие непозиционная система счисления получила в римской системе счисления. Например, число MMIII – здесь каждая единица означает именно единицу, независимо от места (позиции) среди других числе.
Недостаток - сложность записи больших чисел, слишком обширный алфавит.
В позиционной системе счисления количественный эквивалент зависит как от вида самой цифры, так и от ее положения в записи числа.
В позиционной системе счисления используется конечное число символов ai, каждый из которых называется цифрой. Число S различных символов (цифр) в наборе (алфавите) называется основанием системы счисления S. Например, в десятичной системе счисления используются 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Обратите внимания, что максимальное значение цифры в любой системе счисления всегда на 1 меньше, чем основание. Возможно, это связано с тем, что счет начинается с 0, хотя, может быть, у кого-нибудь будут и другие объяснения.
Чтобы в позиционной системе счисления записать количественный эквивалент, больший, чем индивидуальный символ, цифры записывают рядом, и образуется число. В позиционной системе счисления количественный эквивалент (величина) представленный цифрой зависит от позиции - разряда r числа. Значение количественного эквивалента цифры K определяется значением самой цифры, умноженной на некоторый коэффициент "вес". "Вес" - коэффициент, на который нужно умножить цифру, чтобы получить ее истинное значение
| К = aiּ"Вес" = ai ∙ Sr | (1) |
где S – основание системы счисления, r – разряд.
В качестве примера удобно рассмотреть число 1999 в десятичной системе счисления. Самая правая девятка имеет числовой эквивалент, равный 9, следующая за ней девятка имеет числовой эквивалент, равный 9ּ101=90. Последняя цифра девять имеет числовой эквивалент равный 9ּ102=900.
Принцип получения всех натуральных чисел в любой позиционной системе счисления можно сформулировать следующим образом. Нужно взять число 0 и последовательно прибавлять к нему 1. Когда после прибавления к очередному результату сумма будет превосходить максимальную цифру для данной системы счисления (еще говорят, данный разряд заполнился), то нужно к разряду слева добавить единицу, таким образом от цифры мы переходим к числу. Когда в данном разряде сумма превосходит максимальную цифру и нужно прибавлять (переносить) единицу в следующий разряд, говорят, что возник перенос в следующий разряд. При выполнении домашних заданий и контрольных работ (обычно здесь используется авторучка и бумага) эту ситуацию нужно обязательно отмечать дужкой со стрелкой, расположенной над цифрами. Каждая цифра слева показывает, сколько раз заполнялся предыдущий разряд. По-другому, можно сказать, что перенос (заем) переносит в соседний разряд основание системы счисления. Все это легко проверить в десятичной системе счисления. Но поскольку десятичная система радикально не отличается от других позиционных систем, то правила, действующие в этой системе, можно смело переносить в другие системы. Только там, где в десятичной системе приходится использовать число десять, в произвольной системе счисления нужно применять основание этой системы счисления.
Разряды, расположенные слева от разделительной (позиционной) точки (в 10-ой системе счисления она называется децимальной точкой) считаются положительными, начинаются с нуля, и будут обозначаться буквой n. Таким образом, для n разрядного числа старший разряд будет иметь номер n-1. (Интересно, а с чем это связано?) Разряды, расположенные справа от позиционной точки являются отрицательными и обозначаются буквой m. Чем левее разряд, тем он старше, чем правее, тем младшие.
Таким образом, число в позиционной системе счисления с основанием S
| Ns=N(S)=an-1an-2an-3…..a2a1a0.a-1a-2….a-m | (2) |
является просто краткой формой записи полинома
| Ns=an-1Sn-1+ an-2Sn-2+ an-3Sn-3+ …. a2S2+ a1S1+ a0S0+ +a-1S-1+ a-2S-2+ a-3S-3+…+am-2Sm-2+ am-1Sm-1+ amSm=∑aiSi. | (3) |
Здесь уместно привести очень точную цитату [1]: «Когда мы говорим «число 142», нас можно обвинить в неточности, или, по крайней мере, в небрежности. Этой фразой мы хотели сказать «число, представление которого есть 142». Эквивалентно было бы утверждение «число представление которого есть CXLII». Если мы хотим быть точными, то должны признать, что есть различие между числом и одним из его многочисленных представлений…». (Вообще, на мой взгляд, это очень хорошо написанная книжка. Она еще нам очень пригодится при изучении дисциплины «Основы микропроцессорной техники»).
Вообще говоря, читателю, которому все это кажется слишком сложным, следует для облегчения понимания еще раз изучить весьма полезную книгу [2].
В итоге, запишем ключевую для этого раздела формулу, (которую надо сначала вызубрить, а потом, если повезет, и понять):
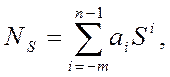
| (4) |
где 0<= ai< S – цифры позиционной системы счисления, n - число цифр правее позиционной точки, m - число цифр левее позиционной точки, S - основание позиционной системы. Очевидно, что (4) является просто краткой формой записи выражения (3).
Для чисел в системах счисления с основанием S < 10 используются арабские цифры, для S > 10 - используются латинские буквы 10-А, 11-В, 12-C, 13-D, 14-E, 15-F.
Какую систему следует выбирать для ЭВМ, μЭВМ, μР, а следовательно и в цифровых схемах? Очевидно, элементы, составляющие микропроцессоры должны иметь S устойчивых состояний.
При выборе S очевидны следующие критерии. Для компактного представления чисел (в этом случае требуется меньше ячеек памяти для хранения чисел, что удешевляет устройство) необходимо применять системы счисления с большим основанием. С другой стороны, чем меньше основание системы (предельный случай S=2), тем проще реализовать базовый элемент и тем дешевле он будет. Общие затраты на оборудование будут складываться из затрат на один базовый элемент и количество разрядов (количество элементов). Их можно представить в следующем виде «Затраты ~ (стоимость элемента)∙(число разрядов числа (число элементов)). Учитывая, что многие наши старшекурсники дружно посещают занятия по менеджменту, предлагается наиболее стремящимся к продвижению в бизнесе из этих данных определить, какое значение S обеспечит минимальные затраты при создании микропроцессоров.








