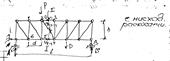
Из уравнения видно, что линия влияния М ( правая ветвь ) строится как линия влияния реакции А с умножением всех ординат на а .
Рассмотрим теперь случай, когда груз расположен слева от сечения, т. е. x ≤ a .
Слева от сечения две силы: реакция А и движущийся единичный груз, а справа только реакция В . Определяем изгибающий момент как сумму сил справа от сечения:
МK = В · b .
Левая ветвь строится как линия влияния реакции В с умножением всех ординат на b .
Левая и правая ветви пересекутся под сечением к , что следует из условия единственности значения изгибающего момента при расположении единичного груза над сечением.
В этом нетрудно убедится, определив ординату линии влияния под сечением к из двух треугольников, которые получились: один при построении правой ветви, а другой при построении левой ветви.
Ордината под сечением будет равна
a · b / l .
1.4.3. Линии влияния поперечной силы
Величина и знак поперечной силы зависят от положения единичного груза относительно сечения к, и поэтому будем строить линию влияния поперечной силы при двух предположениях, как и
для изгибающего момента.
Пусть единичный груз движется справа от сечения
QK = A = ( l – x ) / l .
Это выражение поперечной силы определяет правую ветвь линии влияния. В этом случае поперечная сила положительная, так как стремится повернуть балку по часовой стрелке ( слева – вверх ).
При x = 0 Q = 1 ,
при x = l Q = 0 .
Во втором случае, когда груз движется слева от сечения, выражение поперечной силы будет
QK = – B = – x / l ,
которое определяет левую ветвь. Поперечная сила отрицательная, так как стремится повернуть балку против часовой стрелки ( справа –вверх ).
При x = 0 Q = 0 ,
при x = l Q = – 1 .
Линия влияния поперечной силы приведена на рис. 1.4, в.
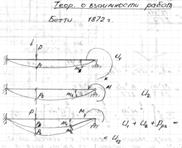
20,Теорема о взаимности работ
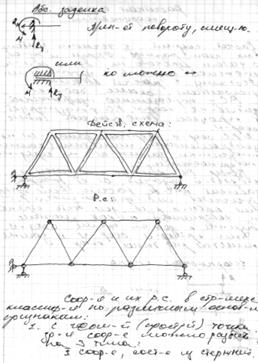
21 Способы образования и условия геометрической неизменяемости плоских ферм.
22,Расчетная схема. Осн. Элементы и их РС.
23. Формула Мора
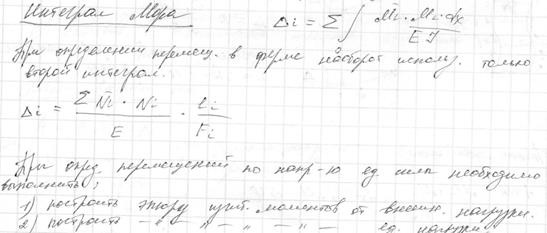
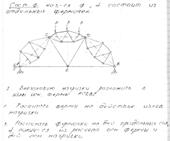
25. Частные случаи равновесия узлов ферм.
26 Определение усилий в стержнях фермы (способ проекций)
27,Невыгоднейшее загружение треугольной ЛВ
28 Расчет составных ферм
29, ЛВ усилий при узловой передаче нагрузки
31,Потенциальная энергия системы
32 Применение уравнений 3-х моментов для расчёта неразрезных балок.
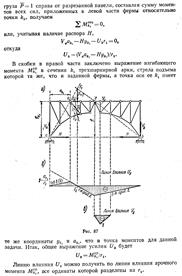
В качестве основной системы необходимо взять систему разрезных балок, полученную из заданной системы включением шарниров в опорные сечения. За неизвестное примем опорный изгиб. Моменты, очевидно, что число их равно числу промежуточных опор при наличии крайних шарнирных опор. Решение выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролёта и значит, большое число побочных перемещений обращается в ноль. Для составления типового канонического уравнения в развёрнутом виде строим эпюры изгибающих моментов в основной системе от внешней нагрузки и единичных усилий. Из рассмотрения этих эпюр вытекает, что типовые канонические уравнения будет трёхчлен следующего вида:
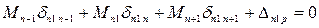
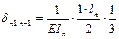
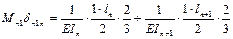
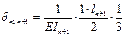
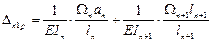
Подставляем: ……
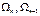- площади эпюр моментов;
an , bn+1 – расстояние от центров тяжести этих эпюр. Умножим правую и левую части на 6EIc получаем:
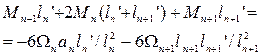
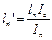
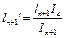
Уравнение 3-х моментов в общем виде. Если I=const
В уравнениях неизвестными являются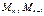 
т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
Если конец защемлён, для применения уравнения трёх моментов вводим дополнитьельный фиктивный пролёт. Для опоры ‘o’ составляем уравнения:
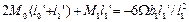
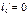
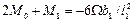
При отсутствии внешней нагрузки на крайнем 1-м пролёте у защемлённого конца: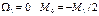 
33,Теорема Клапейрона
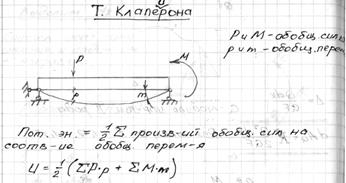
Формулировка теоремы Клапейрона: упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение.
Теорема Клапейрона впервые была сформулирована французским ученым Клапейроном в 1852 г.
|
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ КЛАПЕЙРОНА
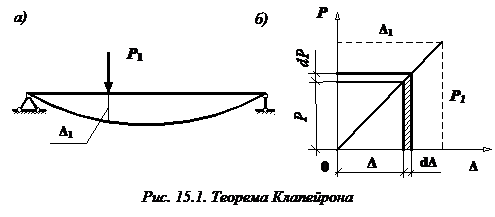
Определим работу, которую совершает сила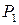 
, действующая, например, на балку, изображенную на рис. 15.1, а.
Будем считать, что нагрузка прикладывается к балке статически, то есть она медленно возрастает от нуля до заданной величины .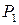
Пусть в некоторый момент сила, достигшая значения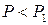 
, вызвала в месте своего приложения прогиб балки, равный 
.
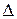Увеличим это значение силы на бесконечно малую величину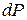 
. Такое изменение нагрузки приведет к дополнительному прогибу 
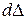. Очевидно, что элементарная дополнительная работа будет равна: 
.
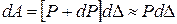Полная работа, совершенная внешней силой, определяется по формуле: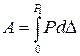 
.Для линейно деформируемой системы (график зависимости между прогибом 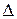и силой P для такой системы показан на рис. 15.1, б) прогиб балки пропорционален внешней нагрузке, то есть 
,
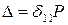где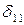 
– коэффициент пропорциональности или перемещение от силы, равной единице 
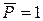. Коэффициент 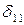часто называют и податливостью системы.
Дифференцируя уравнение 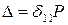, найдем: 
.
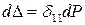Подставляя формулу 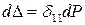в формулу 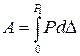и учитывая уравнение 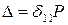, получим: 
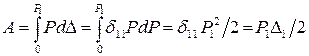,что и требовалось доказать. Полученное выражение соответствует теореме Клапейрона.
34, Построение линий влияния в стержнях балочных ферм статическим способом.
35,Сопоставление арочных и балочных ферм
36, Свойство прямолинейного участка ЛВ.
38, ЛВ М,Q опорных реакций для простых балок с консолями
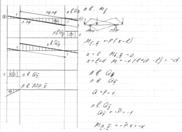
40,ЛВ балки заделанной одним концом
41 Способы образования плоских геометрически неизменяемых систем.
43.Определение усилий в стрежнях ферм.
Для любой статически определимой фермы можно составить 2К уравнений статики (К – число узлов фермы), с помощью которых можно найти опорные реакции и внутренние усилия в ее стержнях от действия внешней нагрузки. При этом в первую очередь обычно определяют опорные реакции. При определении реакций составляют 3 уравнения равновесия для всей фермы в целом.
Для определений внутренних усилий следует выделять сечениями узлы или отдельные части фермы и рассматривать условия их равновесия под действием внешних нагрузок и усилий в рассеченных стержнях. Всего можно составить 2К – 3 таких условий.
Выделение узлов или частей фермы необходимо производить так, чтобы усилия в элементах фермы определялись наиболее просто.
Метод моментной точки. Применяется в тех случаях, когда удается рассечь ферму на две части так, чтобы при этом перерезанными оказались три ее стрежня, направления осей которых не пересекаются в одной точке. Направления осей трех таких перерезанных стержней пересекаются попарно в трех точках, не лежащих на одной прямой. Составляем последовательно уравнения моментов всех сил, действующих на отсеченную часть фермы, относительно этих трех точек, каждый раз будем получать уравнение с одним неизвестным, представляющим собой усилие в рассеченном стержне.
1 разрезаем ферму так, чтобы в разрез кроме данного стержня попали еще 2 других (оси которых не сходятся с ним в одной точке)
2 из уравнения моментов относительно точки пересечения осей этих 2 стержней определяем усилие в данном стержне
При составлении уравнений равновесия все неизвестные усилия в стержне условно считаются положительными, т.е. растягивающими и направленными от узлов. Если после решения уравнений какое – либо усилие окажется отрицательным, значит, оно является сжимающим и направленно к узлу. При расчетах ферм способом моментной точки каждое усилие определяется с помощью одного уравнения с одним неизвестным.
Способ проекций. Применяется в следующих двух вариантах:
1 рассматривается равновесие части фермы (как и при способе моментной точки), когда два из трех рассеченных стержней параллельны друг другу
2 рассматривается равновесие выделяемых из фермы узлов (способ вырезания узлов).
При расчете простейших ферм все усилия можно определить способом проекций, применяя его последовательно к каждому узлу. При этом определение усилий надо считать с узла, в котором сходиться не более двух стержней.
При расчете ферм способом вырезания узлов усилия в ряде стержней можно найти только после предварительного определения усилий в других стержнях. В связи с этим случайная ошибка в определении одного усилия может привести к неправильному определению усилий в целом ряде стержней.
44, Примеры анализа геометрической структуры сооружения
45 Образование и расчет шпренгельных ферм
46,Зависимость усилий в Эл-х фермы от очертания поясов и решетки.
