Расчет ферм на неузловую нагрузку
Способ вырезания узлов позволяет установить некоторые простые правила о значениях продольных
сил в стержнях шарнирных ферм, Если в узле сходятся два стержня и нет узловой нагрузки,то оба стержня не работают, т. е. продольые силы в них равны нулю. Это положение вытекает из уравнений равновесия, выража
ющих сумму проекций сил на оси, перпендикулярные стержням Если в узле сходятся три стержня, причем два из них лежат наодной прямой и нет узловой нагрузки (рис.), то продольная сила в третьем примыкающем стержне равна нулю, а продольные силы в двух остальных стержнях равны 9i между
собой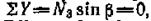 
откуда
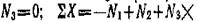
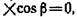откуда n1=n2
13.Теорема о взаимности перемещений
14.Определение усилий в стержнях фермы. Способ моментной точки
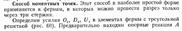
15.Особенности работы ферм. Классификация ферм.
16, Определение перемещений в стержневых системах от изменения температуры
17.Аналитический расчет трех шарнирных арок.
Методические указания
Решению задачи должно предшествовать изучение соответствующего раздела [1-6].
Схему арки надо вычертить, определив по уравнению ее оси достаточное число точек, или, используя соответствующую программу на компьютере. На схему необходимо нанести все заданные размеры и нагрузку.
Ординаты точек оси и углы наклона касательных определяются по следующим уравнениям:
а) при очертании оси по параболе
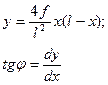(1)
y′= tanφ=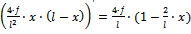 
б) при очертании оси по окружности
,
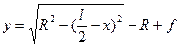где
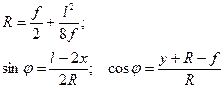(2)
Вычисление значений опорных реакций, моментов, поперечных и продольных сил в заданных точках необходимо иллюстрировать соответствующими формулами. При построении эпюр М, Q и N необходимо придерживаться следующего правила знаков: изгибающий момент считается положительным, если он разгибает арку; продольная сила положительна, если она растягивает арку; поперечная сила положительна, если она вращает один конец арки относительно противоположного почасовой стрелке. Поэтому отрицательные ординаты на эпюре М откладываются вверх с обязательной простановкой знаков.
При построении эпюры Q положительные ординаты откладываются вверх, а при построении эпюры N отрицательные ординаты вниз с обязательной простановкой знаков
Вертикальные опорные реакции в арке определяются как для простой однопролетной балки такого же пролета что и арка, при отсутствии среднего шарнира. Величина распора определяется из равновесия левой (правой) части арки относительно среднего шарнира по формуле
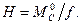(3)
Внутренние силы в любой точке арки могут быть найдены: изгибающий момент М определяется из уравнения моментов относительно точки (х, у); поперечная сила Q, продольная сила N могут быть определены из уравнений проекций сил, действующих на левую или правую часть арки на касательную или нормаль к оси в точке (х, у) по формулам:
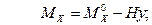
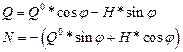, (4)
где -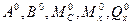 
обозначены соответствующие величины для простой балки.
При вычислении величин М, Q, N и построении соответствующих эпюр арка разбивается на участки. Построение кривой каждого участка осуществляется по трем точкам: начальной, конечной и в середине участка, если на участке нет экстремума. Вычисление величин Q и N выполняется в табличной форме (см. пример 2 расчета арки).
Для построения линий влияния М, Q и N надо сначала построить линию влияния распора и подсчитать значение ее характерной ординаты. При построении линий влияния M, Q, N необходимо использовать формулы (3,4). На окончательных линиях влияния должны быть проставлены числовые значения всех характерных ординат, определение которых должно быть приведено в расчете. Линии влияния надо строить под схемой арки в том же линейном масштабе
18. Определение перемещений в стержневых системах от смещения опор
19. Построение линий влияния опорных реакций М Q для многопролетных балок.
1.4.2. Линии влияния изгибающего момента
Для построения линии влияния изгибающего момента в сечениик, расположенном на расстоянии а от левой опоры, надо получить выражение момента в зависимости от расположения груза справа или
слева от сечения ( Рис. 1.4, б ).
Пусть единичный груз движется справа от сечения, т. е.
а ≤ х ≤ 1 .
Выражение изгибающего момента слева от сечения будет
MK = A · a .