2.Определение перемещений от изменения температуры и смещения опор. Правило верещагина.
1, 7, 42.Расчет неразрезных балок методом фокусов. Моментные фокусные отношения.
При построении эпюры изгибающих моментов от временной нагрузки следует воспользоваться методом моментных фокусных отношений.
Загружается последовательно каждый пролет и вычисляются величины изгибающих моментов на концах каждого загруженного пролета, для этого прежде вычисляется левые 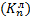 и правые
и правые 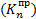 фокусные отношения по формулам.
фокусные отношения по формулам.
Формула для определения левых моментно-фокусных отношений балки
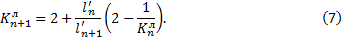
Формула для определения правых моментно-фокусных отношений балки
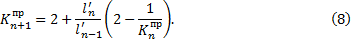
Формулы для определения опорных моментов по концам загруженного пролета
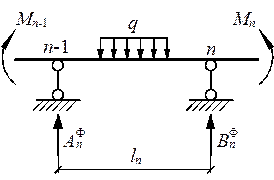
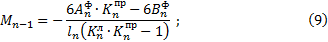
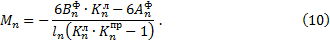
Формула для определения опорных моментов на опорах, расположенных левее опоры 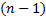 загруженного пролета,
загруженного пролета,

Формула для определения опорных моментов на опорах, расположенных правее опоры 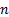 загруженного пролета,
загруженного пролета,

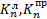 зависят от способа закрепления балки (табл. 11.3).
зависят от способа закрепления балки (табл. 11.3).
Таблица 11.3
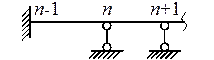
| 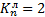
|
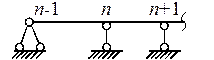
| 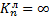
|
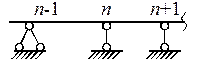
| 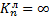
|
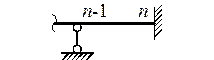
| 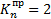
|
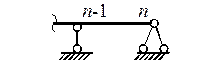
| 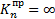
|
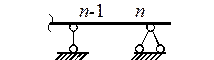
| 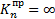
|
Все эпюры изгибающих моментов от временной нагрузки необходимо построить в том же масштабе, что и эпюра изгибающих моментов от постоянной нагрузки. Они строятся одна под другой. Для построения огибающей эпюры изгибающих моментов нужно каждый пролет разбить на три части и подсчитать соответствующие величины ординат изгибающих моментов. Для получения величин максимальных ординат изгибающих моментов ( 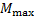 ) в каждом сечении к моменту от постоянной нагрузки (
) в каждом сечении к моменту от постоянной нагрузки ( 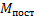 ) прибавляет все положительные ординаты от временной нагрузки, а для получения величин минимальных ординат изгибающих моментов (
) прибавляет все положительные ординаты от временной нагрузки, а для получения величин минимальных ординат изгибающих моментов ( 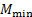 ) в каждом сечении к моменту от постоянной нагрузки (
) в каждом сечении к моменту от постоянной нагрузки ( 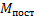 ) – все отрицательные ординаты от временной нагрузки:
) – все отрицательные ординаты от временной нагрузки:
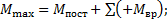 (13)
(13)
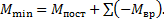 (14)
(14)
Аналогично этому находят 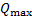 и
и 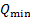
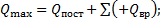 (15)
(15)
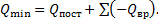 (16)
(16)
Ординаты 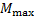 и
и 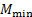 определяют обычно в табличной форме, построение
определяют обычно в табличной форме, построение 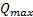 и
и 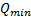 может быть выполнено без таблицы.
может быть выполнено без таблицы.
2.Определение перемещений от изменения температуры и смещения опор. Правило верещагина.



Правило Верещагина

3,Применение уравнений 3-х моментов для расчёта неразрезных балок.
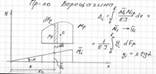
В качестве основной системы необходимо взять систему разрезных балок, полученную из заданной системы включением шарниров в опорные сечения. За неизвестное примем опорный изгиб. Моменты, очевидно, что число их равно числу промежуточных опор при наличии крайних шарнирных опор. Решение выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролёта и значит, большое число побочных перемещений обращается в ноль. Для составления типового канонического уравнения в развёрнутом виде строим эпюры изгибающих моментов в основной системе от внешней нагрузки и единичных усилий. Из рассмотрения этих эпюр вытекает, что типовые канонические уравнения будет трёхчлен следующего вида:
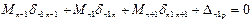
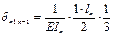
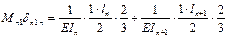
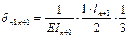
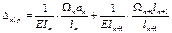
Подставляем: ……
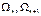 - площади эпюр моментов;
- площади эпюр моментов;
an , bn+1 – расстояние от центров тяжести этих эпюр. Умножим правую и левую части на 6EIc получаем:
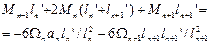
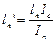
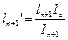
Уравнение 3-х моментов в общем виде. Если I=const
В уравнениях неизвестными являются 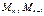 т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
Если конец защемлён, для применения уравнения трёх моментов вводим дополнитьельный фиктивный пролёт. Для опоры ‘o’ составляем уравнения:
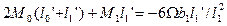
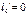
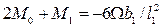
При отсутствии внешней нагрузки на крайнем 1-м пролёте у защемлённого конца: 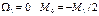
4.Сравнение арки с балкой.Понятие о рациональной оси арки.

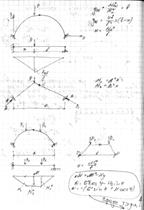
5.39 Построение эпюр изгибающих моментов и поперечных сил для неразрезных балок. Построение объемлющих эпюр.
Если у балки загружен 1-й пролет, то при помощи фокусных отношений очень просто и быстро определяются все опорные моменты.
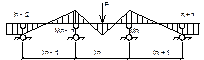
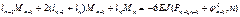
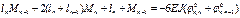 , где
, где 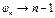
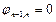
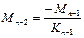
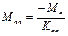
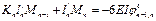
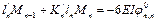
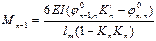
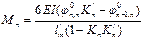 ,
,
где 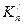 и
и 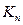 левое и правое фокусные отношения пролета n. Если правая опора шарнирная, то левый опорный момент
левое и правое фокусные отношения пролета n. Если правая опора шарнирная, то левый опорный момент 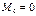
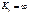 .
.
Правый опорный момент первого загруженного пролёта 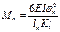
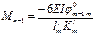 - для крайнего правого нагруженного пролёта
- для крайнего правого нагруженного пролёта
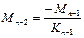
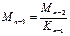
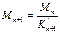
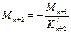
Необходимость нахождения такого сочетания пост-х и врем-х нагрузок, которые вызывают в различных сечениях наибольшие и наименьшие изгибающие моменты и поперечные силы приводящие к необходимости построения обьемляющие эпюр.
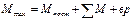
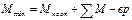
Аналогично находят 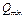 и
и 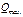
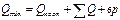
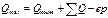
Ординаты 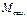 и
и 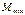 определяют обычно по табличной формуле, построение
определяют обычно по табличной формуле, построение 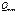 и
и 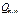 может быть выполнено без таблиц.
может быть выполнено без таблиц.
6.Теорема о взаимности реакций.

8 Определние усилий в стержнях фермы. Способ вырезания узлов.


9 Построение линий влияния опорных реакций и внутренних усилий для 3-х шарнирных арок. 
10.Анализ неизменяемости ферм способом нулевых нагрузок.
Анализ неизменяемости ферм
 Способ нулевой нагрузки. Способ нулевой нагрузки значительно проще предыдущего общего метода. Сущность способа нулевой нагрузки заключается в следующем.
Способ нулевой нагрузки. Способ нулевой нагрузки значительно проще предыдущего общего метода. Сущность способа нулевой нагрузки заключается в следующем.
Рассмотрим ферму, освобожденную от нагрузки. Если при действии конечной нагрузки в неизменяемой ферме все усилия Xt должны иметь конечные значения, то при нулевой нагрузке усилия
в статически определимой ферме должны иметь нулевые значения. Такой ответ для всех усилий свидетельствует о неизменяемости данной фермы. Если же в каком-либо стержне или в группе стержней фермы усилия X; оказываются неопределенными, система изменяема.
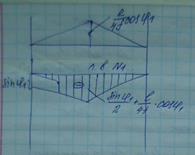
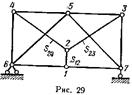
В качестве примера проанализируем ферму по рис. 29. В этой ферме нет ни одного узла, где сходятся
два стержня. Докажем, что при отсутствии нагрузки усилия во всех стержнях фермы равны нулю.
Сначала выделим узел /; проектируя все усилия, действующие на этот узел, на вертикаль, найдем, что усилие 5,2 = 0. Затем вырежем узел 2, в котором имеется два новых стержня и нет нагрузки, поэтому 524 = 0, S2S — 0. После этого перейдем к узлам 3 и 4 и, удовлетворяя тому же условию (в каждом узле два новых стержня,
а усилие в среднем стержне равно нулю), получим:
S4. = 0. S4S-0, 5М = 0,5„ = 0. Теперь рассмотрим узел 5:
5„ = 0, S.- = 0
Выделяя узлы 7 и б, находим:
S,, = 0. 5,й = 0.
Усилия во всех стержнях данной фермы при отсутствии нагрузки нулевые, следовательно, ферма неизменяема
Значительно проще задача решается рассмотрением трех дисков (два треугольника и стержень 1 — 2).
11.Определение усилий по линия влияния от действия сосредоточенных сил и распределенной нагрузки.


12.Расчет ферм на внеузловую нагрузку

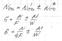
Или








