Для определения С v для каждого члена ряда вычисляются: модульный коэффициент , (К i – 1) и Σ(К i – 1)2, которые заносятся соответственно, в графы 6,7,8 таблицы 1.1.

Дата: 2025-06-02; Просмотры: 13
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Вычисления выполняются с точностью: К i и (К i – 1) до 0,01; (К i – 1)2 до 0,0001.

Для контроля вычисляют: ΣК i, которая должна быть равной или близкой n; Σ(К i – 1) – должна быть близкой или равной нулю. Коэффициент вариации определяется по формуле:

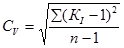
2.1.3 Коэффициент асимметрии Cs:

Коэффициент асимметрии для приближенных расчетов принимается, как С s = 2С v.

Коэффициенты С s и С v вычисляются с точностью до 0,01.

2.2 Определить ординаты теоретической кривой обеспеченности для значений обеспеченности: Р = 0,1; 1; 5; 10; 20; 30; 40; 50; 60; 70; 80; 90; 95;99; 99,9%.

Для принятых величин обеспеченности вычисляются модульные коэффициенты:

,

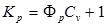где: ФР – отклонение от среднего значения ординаты кривой обеспеченности при С v =1, принимается по таблице Фостера - Рыбкина (приложение 3) по ранее вычисленному С s и принятым величинам Р%.

2.3 Вычислить расходы воды заданных процентов обеспеченности:

,

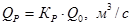где: 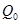– средний многолетний расход воды, м3/с.

Вычисления занести в таблицу 2.1.

Таблица 2.1 – Вычисление ординат теоретической кривой обеспеченности средних годовых расходов воды (пример оформления)

Р% Фр Фр ∙С v Кр Q р , м3/с
1 2 3 4 5
0,1        
1,0        
5        
10        
и т.д. (п.2.2)        
99        
99,9        

 

2.3 По вычисленным значениям Qp и принятым значениям Р (графы 1 и 5 таблицы 2.1) построить кривую обеспеченности расходов воды черным цветом на той же клетчатке вероятностей, что и эмпирическая кривая.

2.4 Дать заключение о степени совпадения обеих кривых и о возможности использования теоретической кривой для экстраполяции эмпирической кривой обеспеченности.

2.5 Дать оценку достаточности ряда лет измеренных расходов воды, использованного в задании для расчёта обеспеченности.

Критерии достаточности ряда:

средняя квадратичная погрешность в определении среднего многолетнего расхода воды (нормы):

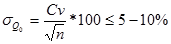
средняя квадратичная погрешность в определении коэффициента вариации:

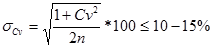
где n – число лет.