2. Деление отрезка прямой на любое число равных частей
| ЛЕКЦИЯ. Деление отрезка прямой и окружности на равные части |
ПЛАН:
1.Деление отрезка на две равные части
2. Деление отрезка прямой на любое число равных частей
3.Деление окружности на 3, 6, 12 и т, д. равных частей
- Деление отрезка на две равные части
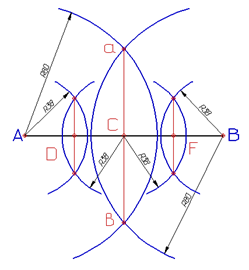
| Из концов отрезка А и В циркулем проводят две дуги окружности радиусом R, несколько большим половины отрезка, до взаимного пересечения в точках а и в. Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части. Проделав подобные построения для отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части. |
|
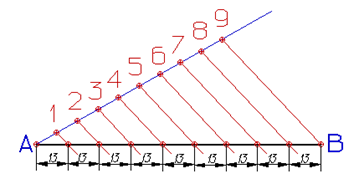
| Пусть отрезок АВ требуется разделить на 9 равных частей. Для этого из любого конца отрезка (из точки А) проведем под острым углом к отрезку прямую линию, на которой от точки А измерительным циркулем откладываем 9-ть равных отрезков произвольной величины. Точку 9соединяем с точкой В (концом данного отрезка) прямой. Из точек 1, 2, ... 8 проведем ряд прямых параллельных прямой 9А, которые пересекая отрезок АВ разделят его на 9 равных частей. |
Построение прямой, перпендикулярной к отрезкуMN и проходящей через точку М (рисунок 14). Вне отрезкаMNвыбирают произвольную точкуО так, чтобы уголOMN был приблизительно равен 45 – 60°. Из центраО проводят окружность радиусомОМ, которая пересечет заданный отрезок в точкеА. ТочкиA иО соединяют прямой и продолжают ее до пересечения с окружностью в точкеВ. Прямая, проведенная через точкиВиM, будет перпендикулярна к заданной в силу того, что уголВMА– прямой как угол, вписанный в окружность и опирающийся на ее диаметр.
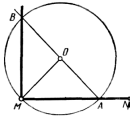
Рисунок 14
Построение перпендикуляра к прямойMN из точкиА, расположенной внеэтой прямой (рисунок 15). Из точкиAкак из центра произвольным радиусомR проводят дугу, пересекающую заданную прямую в точкахO1 иO2. Тем же радиусомR из полученных точек проводят дуги до их взаимного пересечения в точкеD. Прямая, проведенная через точкиАиD, перпендикулярна к заданной.
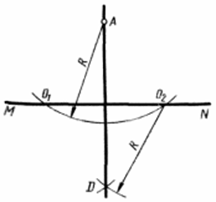
Рисунок 15
2.1.2 Построение параллельных прямых
Провести прямую, параллельную заданной прямой MN, через точку А, расположенную вне этой прямой (рисунок 16, а). Из точки A проводят окружность радиусом R, пересекающую прямую MN в точках В и С. Отодной из них, например точки C, напрямой MN откладывают в любую сторону отрезок, равный радиусу R, и получают точку D. Из точки D тем же радиусом проводят дугу до пересечения ее с окружностью в точке E. ПрямаяAE параллельнаMN, так как отрезкиAE иCD являются противоположными сторонами ромбаACDE.
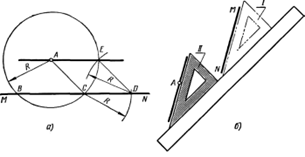
Рисунок 16
При наличии угольника и линейки задача решается проще (рисунок 16, б). К прямой MN прикладывают угольник гипотенузой (положение угольника I), а к его катету – линейку.
Придерживая линейку левой рукой, правой угольник передвигают до совпадения его гипотенузы с точкой A(положение угольникаII) и через нее проводят прямую, параллельную заданной.
Провести прямую, параллельную заданной прямой МН и отстоящую от нее на расстоянии а (рисунок 17). Через произвольную точкуВна прямойMNпроводят прямуюAB, перпендикулярную к заданной. На перпендикуляре от точки В откладывают отрезок BC, равный заданному расстоянию а. Через точку С спомощью угольника и линейки проводят прямую CD, параллельную заданной. Отрезок BC = а можно отложить на перпендикуляре в обе стороны, поэтому задача имеет два ответа.
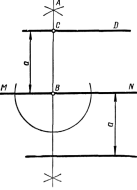
Рисунок 17
3. Деление окружности на 3, 6, 12 и т, д. равных частей
Деление окружности на 3, 6, 12 и т, д. равных частей, а также построение соответствующих правильных вписанных многоугольников осуществляют следующим образом. В окружности проводят два взаимно перпендикулярных диаметра1–2 и3–4 (рисунок 29 а). Из точек1 и2 как из центров описывают дуги радиусом окружностиRдо пересечения с ней в точкахА, В, С иD. ТочкиA,B,1, С, D и2делят окружность на шесть равных частей. Эти же точки, взятые через одну, разделят окружность на три равные части (рисунок 29, б). Для деления окружности на 12 равных частей описывают еще две дуги радиусом окружности из точек3 и4 (рисунок 29, в).
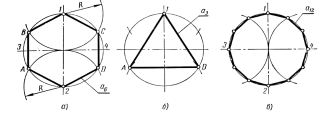
а б в
Рисунок 29
Построить правильные вписанные треугольник, шестиугольник и т. д. можно также с помощью линейки и угольника в 30 и 60°. На рисунке 30 приведено подобное построение для вписанного треугольника.
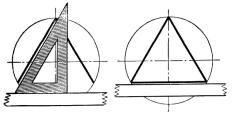
Рисунок 30
Деление окружности на семь равных частейи построение правильного вписанного семиугольника (рисунок 31) выполняют с помощью половины стороны вписанного треугольника, приблизительно равной стороне вписанного семиугольника.
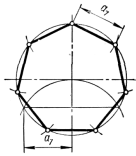
Рисунок 31
Для деления окружности на пять или десятьравных частейпроводят два взаимно перпендикулярных диаметра (рисунок 32, а). РадиусOA делят пополам и, получив точкуВ, описывают из нее дугу радиусомR=BC до пересечения ее в точкеD с горизонтальным диаметром. Расстояние между точкамиC иD равно длине стороны правильного вписанного пятиугольника (а5), а отрезокOD равен длине стороны правильного вписанного десятиугольника (а10). Деление окружности на пять и десять равных частей, а также построение вписанных правильных пятиугольника и десятиугольника показаны на рисунке 32, б. Примером использования деления окружности на пять частей является пятиконечная звезда (рисунок 32, в).
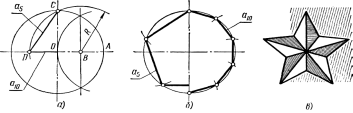
а б в
Рисунок 32
На рисунке 33 приведен общий способ приближенного деления окружности на равные части. Пусть требуется разделить окружность на девять равных частей. В окружности проводят два взаимно перпендикулярных диаметра и вертикальный диаметрAB делят на девять равных частей с помощью вспомогательной прямой (рисунок 33, а). Из точкиBописывают дугу радиусомR =AB, и на пересечении ее с продолжением горизонтального диаметра получают точкиСиD. Из точекC иD через четные или нечетные точки деления диаметраAB проводят лучи. Точки пересечения лучей с окружностью разделят ее на девять равных частей (рисунок 33, б).
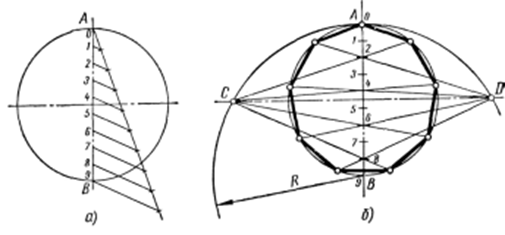
Рисунок 33
При построении необходимо учитывать, что такой способ деления окружности на равные части требует особенно большой точности выполнения всех операций.
Задание для самостоятельной работы «Деление окружности на равные части»
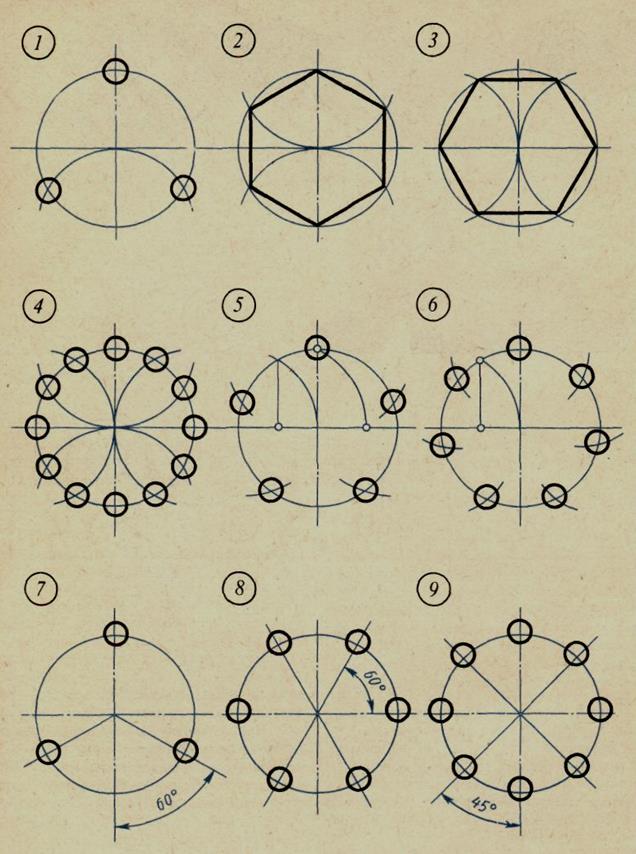
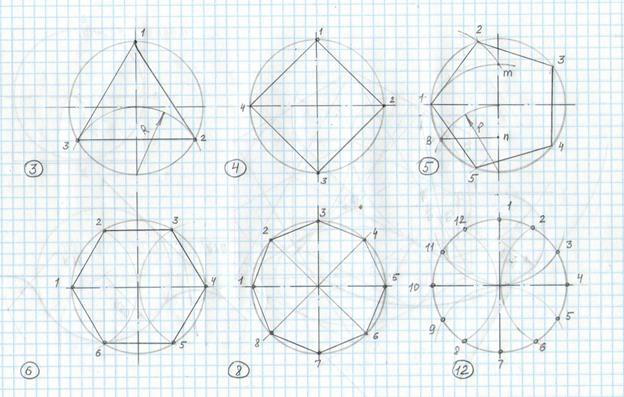
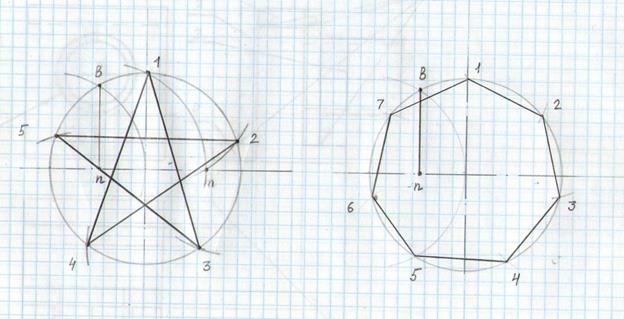
Рисунок 1 – Образец выполнения работы








