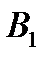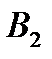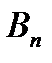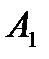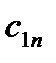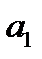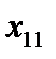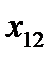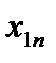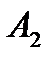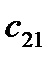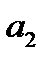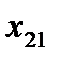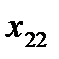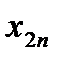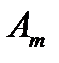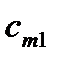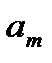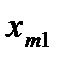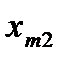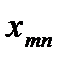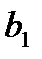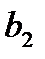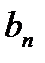Формула 11 . Транспортная задача
Система содержит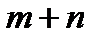 
уравнений с 
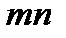неизвестными. Её особенность состоит в том, что коэффициенты при неизвестных всюду равны единице. Кроме того, все уравнения системы могут быть разделены на две группы: первая группа из т первых уравнений (“горизонтальные” уравнения) и вторая группа из п остальных уравнений (“вертикальные” уравнения). В каждом из горизонтальных уравнений содержатся неизвестные с одним и тем же первым индексом (они образуют одну строку матрицы перевозок), в каждом из вертикальных уравнений содержатся неизвестные с одним и тем же вторым индексом (они образуют один столбец матрицы перевозок). Таким образом, каждая неизвестная встречается в системе (11) дважды: в одном и только одном горизонтальном и в одном и только одном вертикальном уравнениях.
Для решения транспортной задачи необходимо кроме запасов и потребностей знать также и тарифы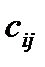 
, т. е. стоимость перевозки единицы груза с базы 
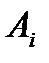потребителю 
.
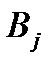Совокупность тарифов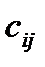 
также образует матрицу, которую можно объединить с матрицей перевозок и данными о запасах и потребностях в одну таблицу:
| Таблица 2 . Таблица стоимостей | ||||||||||
| Пункты Отправления | Пункты назначения | Запасы | ||||||||
|
|
| … |
| |||||||
|
|
| 
| 
| … |
|
| ||||
|
|
|
| ||||||||
|
|
| 
| … |
| 
|
| ||||
|
|
|
| ||||||||
| … | … | … | … | … | … | |||||
|
|
| 
| … |
| 
|
| ||||
|
|
|
| ||||||||
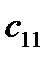
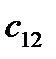
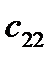
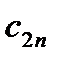
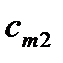
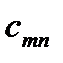
| Потребности |
|
| … |
| 
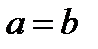или
| |||||
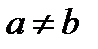
Сумма всех затрат, т. е. стоимость реализации данного плана перевозок, является линейной функцией переменных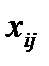 
:
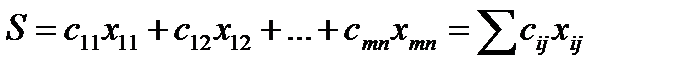(12)
Требуется в области допустимых решений системы уравнений (11) найти решение, минимизирующее линейную функцию (12)
Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без симплекс-таблиц. Решение можно получить путем некоторых преобразований таблицы перевозок. Эти преобразования соответствуют переходу от одного плана перевозок к другому. Но, как и в общем случае, оптимальное решение ищется среди базисных решений. Следовательно, мы будем иметь дело только с базисными (или опорными) планами. Так как в данном случае ранг системы ограничений-уравнений равен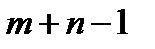 
то среди всех 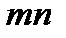неизвестных 
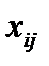выделяется 
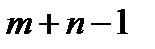базисных неизвестных, а остальные 
· 
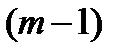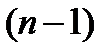
неизвестных являются свободными. В базисном решении свободные неизвестные равны нулю. Обычно эти нули в таблицу не вписывают, оставляя соответствующие клетки пустыми. Таким образом, в таблице перевозок, представляющей опорный план, мы имеем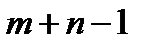 
заполненных и 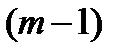· 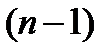пустых клеток.