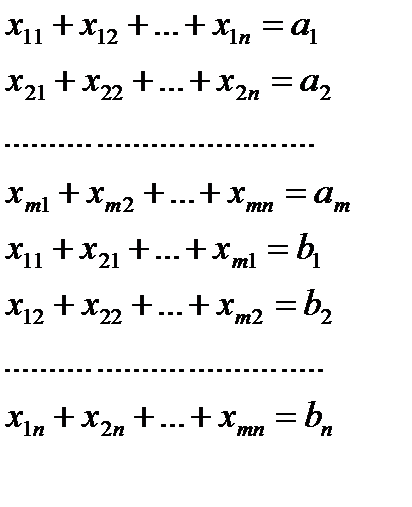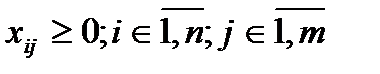Каноническая форма задачи линейного программирования
Математическая модель задачи должна иметь каноническую форму.
Если система ограничения состоит только из уравнения и все переменные удовлетворяют условию неотрицательности, то задача имеет каноническую форму.
Если в системе есть хотя бы одно неравенства или какая–либо переменная неограниченна условию неотрицательности, то задача имеет стандартную форму. Чтобы привести задачу к каноническому виду надо:
перейти от неравенств к уравнению следующим образом: в левую часть неравенств вводим дополнительную переменную с коэффициентом (+1) для неравенства (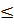 
) и (-1) для неравенства ( 
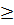) дополнительные переменные не наложены целевые неотрицательности, то её заменяют разностью двух неотрицательных переменных, то есть:
= 
– 
( 
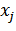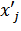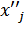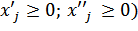(3)
Общий вид канонической формы:
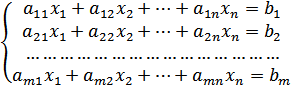(4)
Решение задачи линейного программирования симплекс-методом
Симплекс-метод известен с 1947 года, когда появилась первая публикация Джона Данцига, посвященная этому методу. В советской литературе 60-80-х гг. прошлого столетия этот метод был известен также как метод последовательного улучшения плана.
За прошедшие с тех пор годы было предложено не только много разновидностей симплекс-метода, учитывающих особенности различных подклассов задачи ЛП (блочные задачи, задачи со слабо заполненной матрицей условий A ={ai, j}), но и несколько принципиально иных методов решения задачи ЛП. Некоторые из предложенных методов в теоретическом плане, например, с точки зрения характеристики сложности алгоритма, превосходят симплекс-метод (известно, что симплекс-метод обладает экспоненциальной сложностью, т.е. имеет экспоненциальную оценку трудоемкости на всем классе задач ЛП, тогда как такие алгоритмы, как метод эллипсоидов Хачияна (советского математика) и метод Крамаркара (американского исследователя) характеризуются полиномиальной сложностью). И, тем не менее, по утверждению многих специалистов в теории линейного программирования симплекс-метод и после десятилетий всесторонней апробации с точки зрения алгоритмической реализации и универсальности применимости на классе задач ЛП остается наиболее предпочтительным, а потому наиболее распространенным методом решения задач ЛП.
Симплексный метод – это метод последовательного улучшения плана (решения), наиболее эффективный и применяется для решения любой задачи линейного программирования.
Название метода от латинского simplecx – простой т.к. из начального область допустимых решений задачи имела простейший вид. Идеи метода предложил российский математик Контарович Л.В. в 1939 году и затем эту идею развил и разработал Дж. Данциг в 1949 году.
Симплексный метод позволяет за конечное число шагов либо найти оптимальное решение либо доказать что его нет.
1.5 Задача о распределении ресурсов
Постановка задачи
Имеется некоторое количество ресурсов, под которыми можно понимать денежные средства, материальные ресурсы (например, сырье, полуфабрикаты, трудовые ресурсы, различные виды оборудования и т. п.). Эти ресурсы необходимо распределить между различными объектами их использования (по отдельным промежуткам планового периода или по различным объектам) так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить, например, прибыль, фондоотдача (задачи максимизации) или суммарные затраты, себестоимость, время выполнения данного объема работ и т. п. (задачи минимизации).
Вообще говоря, подавляющее число задач математического программирования вписывается в общую постановку задачи оптимального распределения ресурсов. Естественно, что при рассмотрении моделей и вычислительных схем решения подобных задач методом ДП необходимо конкретизировать общую форму задачи распределения ресурсов.
Опишем типичную задачу распределения ресурсов в общем виде.
Имеется начальное количество средств 
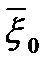, которое необходимо распределить в течение n лет между s предприятиями. Средства 
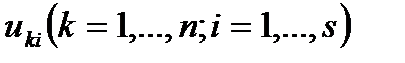, выделенные в k-м году i-му предприятию, приносят доход в размере 
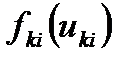и к концу года возвращаются в количестве 
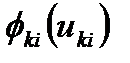. В последующем распределении доход может либо участвовать (частично или полностью), либо не участвовать.
Требуется определить такой способ распределения ресурсов (количество средств, выделяемых каждому предприятию в каждом плановом году), чтобы суммарный доход от s предприятий за n лет был максимальным.
Следовательно, в качестве показателя эффективности процесса распределения ресурсов за n лет принимается суммарный доход, полученный от s предприятий:
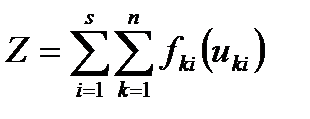. (5)
Количество ресурсов в начале k-го года будем характеризовать величиной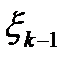 
(параметр состояния). Управление на k-м шаге состоит в выборе переменных 
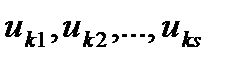, обозначающих ресурсы, выделяемые в k-м году i-му предприятию.
Если предположить, что доход в дальнейшем распределении не участвует, то уравнение состояния процесса имеет вид
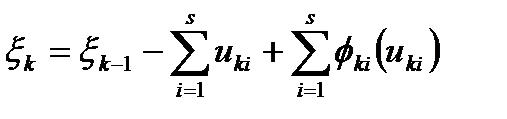(6)
Если же некоторая часть дохода участвует в дальнейшем распределении в каком-нибудь году, то к правой части равенства прибавляется соответствующая величина.
Требуется определить ns неотрицательных переменных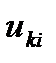 
, удовлетворяющих условиям (2.2) и максимизирующих функцию (2.1).
Вычислительная процедура ДП начинается с введения функции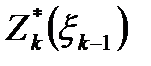 
, обозначающей доход, полученный за п— k+1 лет, начиная с k-го года до конца рассматриваемого периода, при оптимальном распределении средств между s предприятиями, если в k-м году распределялось 
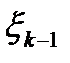средств. Функции 
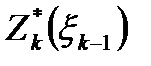для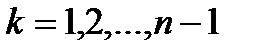 
удовлетворяют функциональным уравнениям (1.5), которые запишутся в виде
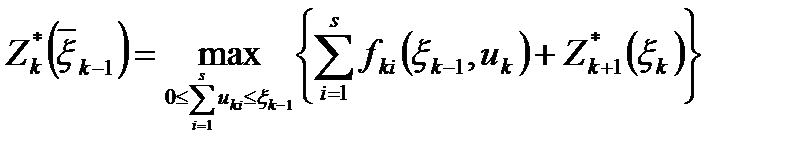(7)
При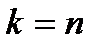 
согласно (1.5) получаем
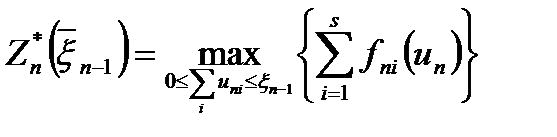. (8)
Далее необходимо последовательно решить уравнения (7) и (8) для всех возможных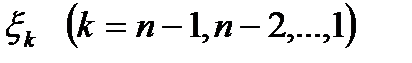 
. Каждое из этих уравнений представляет собой задачу на оптимизацию функции, зависящей от s переменных. Таким образом, задача с ns переменными сведена к последовательности n задач, каждая из которых содержит s переменных. В этой общей постановке задача по-прежнему сложна (из-за многомерности) и упростить ее, рассматривая как ns-шаговую задачу, в данном случае нельзя. В самом деле, попробуем это сделать. Пронумеруем шаги по номерам предприятий сначала в 1-м году, затем во 2-м и т. д.:
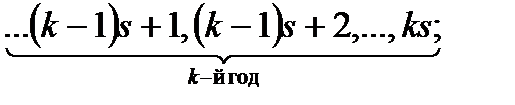
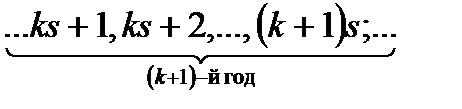
и будем пользоваться одним параметром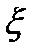 
для характеристики остатка средств.
В течение k-го года состояние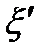 
к началу любого шага 
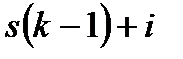(i=l, 2, .... s) определится по предыдущему состоянию 
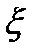с помощью простого уравнения 
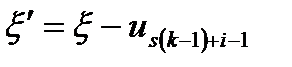. Однако по истечении года, т. е. к началу следующего года, к наличным средствам необходимо будет добавить 
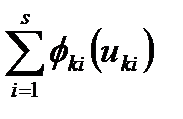средств и, следовательно, состояние 
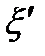в начале 
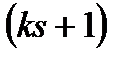-го шага будет зависеть не только от предшествующего ks-го состояния, но и от всех s состояний и управлений за прошлый год. В результате мы получим процесс с последействием. Чтобы исключить последействие, приходится вводить несколько параметров состоянии; задача на каждом шаге остается по-прежнему сложной из-за многомерности.
1.6 Транспортная задача
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом.
В общей постановке транспортная задача состоит в отыскании оптимального плана перевозок некоторого однородного груза с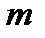 
баз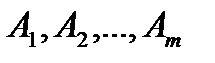 
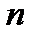потребителям 
.
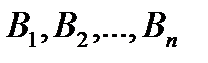Различают два типа транспортных задач: по критерию стоимости и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени).
Обозначим количество груза, имеющегося на каждой из 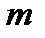баз (запасы), соответственно 
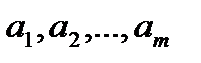,а общее количество имеющегося в наличии груза– 
:
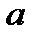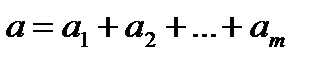; (9)
заказы каждого из потребителей (потребности) обозначим соответственно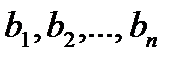 
, а общее количество потребностей – 
:
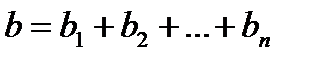, (10)
Тогда при условии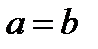 
мы имеем закрытую модель, а при условии 
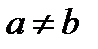– открытую модель транспортной задачи.
Очевидно, в случае закрытой модели весь имеющийся в наличии груз развозится полностью, и все потребности заказчиков полностью удовлетворены; в случае же открытой модели либо все заказчики удовлетворены и при этом на некоторых базах остаются излишки груза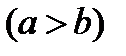 
, либо весь груз оказывается израсходованным, хотя потребности полностью не удовлетворены 
.
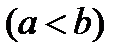План перевозок с указанием запасов и потребностей удобно записывать в виде следующей таблицы, называемой таблицей перевозок:
| Таблица 1 . Таблица перевозок | |||||
| Пункты Отправления | Пункты назначения | Запасы | |||
| 
| … | 
| ||
| 
| 
| … | 
| 
|
| 
| 
| … | 
| 
|
| … | … | … | … | … | … |
| 
| 
| … | 
| 
|
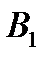
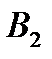
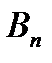
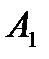
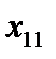
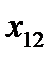
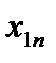
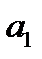
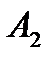
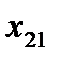
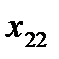
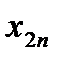
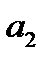
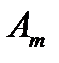
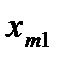
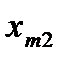
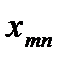
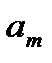
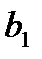
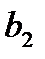
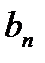
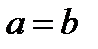| Потребности | 
| 
| … | 
|
или
|
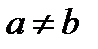
Переменные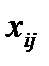 
означает количество груза, перевозимого с базы 
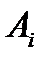потребителю 
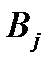: совокупность этих величин образует матрицу (матрицу перевозок).
Очевидно, переменные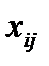 
должны удовлетворять условиям:
