Рисунок 1 . Граф поиска дополнительного решения
определяет задачу нахождения удовлетворительных решений. Для наглядной иллюстрации этой задачи рассмотрим последовательность выполняемых в процессе решения операций, отобразим её ориентированным графом (рисунок 1). Маршрут из начальной вершины О в конечную вершину F, удовлетворяющий для каждого h Î H и управления u0 Î Uf, является решением задачи.
Задачу принятия оптимальных решений сформулируем следующим образом. Дан элемент y0 Î Y и подмножество Uf. Требуется определить такой элемент u* Î Uf и соответствующий ему элемент x* Î X, при которых для всех h Î H и для всех u Î Uf (u ¹ u*) будет выполняться неравенство
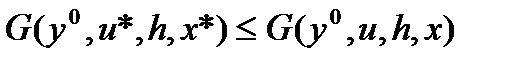
1.3 Многостадийный процесс
Многостадийные процессы – это такие процессы, в которых решения принимаются на каждой из последовательных стадий.
При постановке и решении задачи формулируется некоторый критерий, подлежащий удовлетворению, рассматриваемый процесс разбивается на стадии во времени или в пространстве и на каждой стадии принимаются решения, при которых достигается поставленная цель.
При рассмотрении вопросов динамического программирования принята следующая терминология:
а) стадия – единичный элемент, на которые делится весь процесс во времени или в пространстве; ступень – часть стадии. В любом случае стадия и ступень – это математические конструкции, применяемые для представления в дискретном виде непрерывной переменной;
б) состояние системы характеризуется совокупностью переменных, последние описывают состояние системы на любой стадии процесса;
в) переход от стадии к стадии и от состояния к состоянию описывается функциональными уравнениями;
г) стратегия определяется системой решений функционального уравнения; оптимальная стратегия выражается системой функций, максимизирующих правую часть уравнения.
Стадии процесса могут быть однородными и неоднородными. Процесс с однородными стадиями представляет собой последовательное изменение состояния объекта во времени, он состоит из последовательности однотипных стадий.
Процесс с неоднородными стадиями состоит из разнородных стадий. Состояние отдельной стадии характеризуется совокупностью величин, которые называются выходом или переменными состояния стадии. Если выход стадии является входом для следующей стадии, то для последней совокупность выходных переменных предыдущей стадии определяет состояние входа.
Кроме входных и выходных переменных на каждой стадии определяется группа управляющих переменных (управление), а также предполагается известным математическое описание каждой стадии.
Рассматриваемый многостадийный процесс условно изображается функциональной схемой, изображенной на рисунке 2.
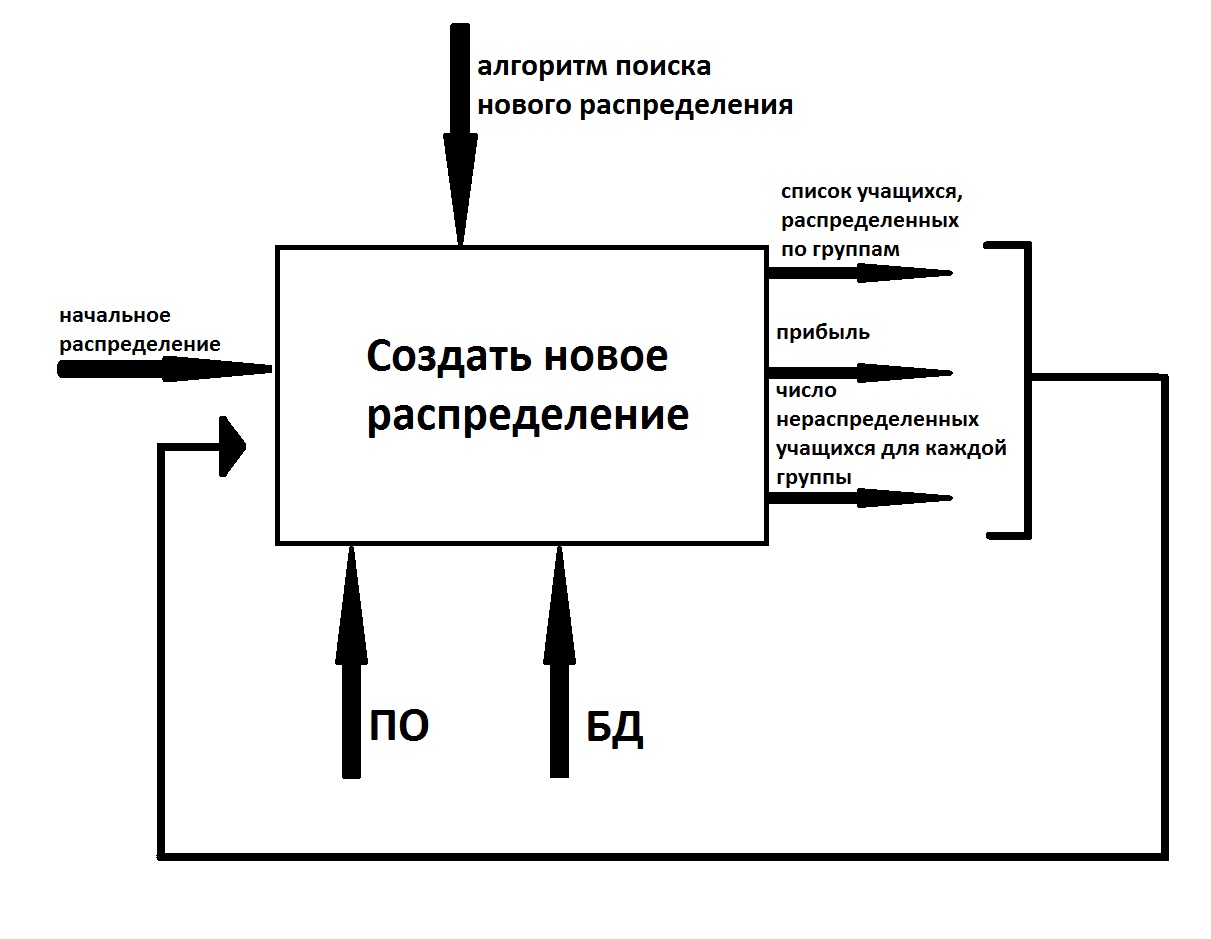
Рисунок 2 . Функциональная схема
1.4 Задача линейного программирования
Перед решением задачи составляем её математическую модель.
Математическая модель – это совокупность соотношений состоящие из линейной целевой функции и линейных ограничений на переменную.
Принцип составления математической модели.
1. Выбирают переменные задачи.
Переменными задачи называются величины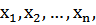 
которые полностью характеризуют экономический процесс, описанный в задачи. Обычно записываются в виде вектора X = ( 
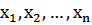) Причём 
)
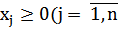2. Составляют систему ограничения задачи.
Система ограничений – это совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которая следует из ограниченности экономических условий задачи.
В общем виде система записывается в виде
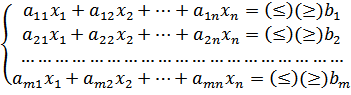(1)
3. Задают целевую функцию.
Целевая функция – это функция Z(X) которая характеризует качество выполнения задачи, экстремум которой надо найти. В общем виде целевая функция записывается Z(X) =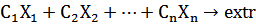 
(max, min)
т.о. математическая модель имеет вид найти переменные задачи
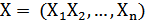удовлетворяющие системе ограничений: 
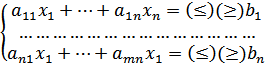(2)
и условию неотрицательности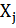 
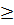0 (j = 
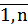), которая обеспечивает экстремум целевой функции Z ( Y ) =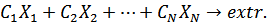 
Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности.
Множество допустимых решений образует область допустимых решений задачи (ОДР).
Оптимальным решением называется допустимое решение задачи, при котором целевая функция достигает экстремума.